knapsack (4000 ms)： 

This question , If you use the idea of backpacking , The one-dimensional list is used to record whether the corresponding position can be reached , Such as dp[4] Indicates whether it is possible to start from ( Indexes 0) Reach index 4 The location of

class Solution(object):
def canJump(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
dp = [False for _ in range(len(nums))]
dp[0] = True
for loc, limit in enumerate(nums[:-1]):
if dp[loc]:
# Determine whether the current position is reachable
for pace in range(1, limit + 1):
# Enumerate jump distances
if loc + pace < len(nums) - 1:
dp[loc + pace] = True
else:
# prune ： The current position can reach the destination directly
return True
return dp[-1]

Suppose that in the worst case, each value in the array is close to its length , Then the worst time complexity of this algorithm is O(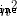), You can't pass the test without pruning

Dynamic programming (100 ms)：

Another idea of dynamic programming is , A one-dimensional list is used to represent the longest distance that the corresponding position can be moved . The equation of state transfer is as follows ：

dp[idx] = max([ dp[idx - 1] - 1, num[idx] ])

And then to [3, 2, 1, 0, 4] For example , Just deduce the boundary conditions

class Solution(object):
def canJump(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
for idx in range(1, len(nums)):
state_1 = nums[idx - 1] - 1
state_2 = nums[idx]
if state_1 >= 0:
# This position can reach
nums[idx] = max([state_1, state_2])
else:
return False
if len(nums) <= 1 or nums[-2]:
return True
else:
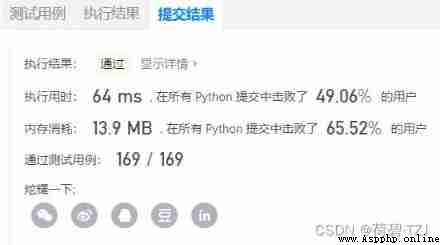
return False

Compared with backpacking , The time complexity has been reduced to O(n), But the test results are still not ideal

greedy (65 ms)：

The idea is simple , Look directly at the comments of the code

class Solution(object):
def canJump(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
max_idx = 0
# Index of the farthest point reachable
target = len(nums) - 1
# Index of end point
for loc, pace in enumerate(nums):
if max_idx >= loc:
# Confirm the current point ( Indexes loc) It can reach
max_dist = max([loc + pace, max_idx])
# Compare and take the best
if max_dist >= target:
return True
return False

I think so. , In many cases , Whether it is time complexity or space complexity , Greed is better than dynamic programming . But feeling greedy is a little mysterious , More practice