Exchange change for Python - Backpack

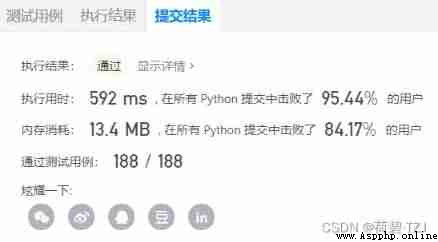
This problem needs a backpack . The first time I did this problem , A two-dimensional matrix is used to record the state —— The test results are touching

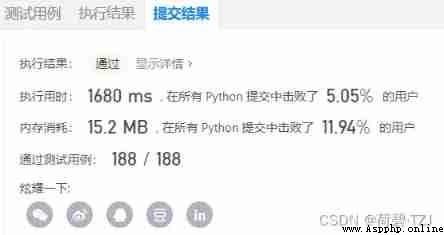
Before I change the spatial complexity from O(mn) drop to O(n) When , While simplifying the code , The execution time has also been reduced by about half , So It is also important to reduce space complexity Of

From the basic framework , Then consider the boundary conditions

Use a one-dimensional list bag To record the status ,bag[0] Means to fold to 1￥ The minimum number of coins required ,bag[amount - 1]  Indicates the minimum number of coins needed to fold to the total amount . Because the optimal operation is min, therefore bag The initial value of inf = amount + 1

hypothesis ：coins = [2, 1, 5, 3],amount = 6, be bag = [inf, inf, inf, inf, inf, inf]

The first coin is special , Now the face value is 2 Of , Update bag = [inf, 1, inf, 2, inf, 3]

When we think about the remaining coins, we are thinking about bag Update if you want to , Now the face value is 1 Of , If you update as above , be bag = [1, 2, 3, 4, 5, 6], Obviously, it breaks the optimal state

If so updated ：

• bag[0] = 1, One 1 The coin of is the best
• bag[0 + 1] = min([ bag[0 + 1], bag[0] + 1 ]) = min([1, 1 + 1]) = 1, One 2 The coin of is the best
• bag[1 + 1] = min([ bag[1 + 1], bag[1] + 1 ]) = min([ inf, 1 + 1 ]) = 2, One 1 The coin of + One 2 The coin of is the best

Pass it on like this , While keeping the best step by step ,bag[-1] Would be the best answer

class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
inf = amount + 1
bag = [inf for _ in range(amount)]
for idx, coin in enumerate(coins):
if idx:
# When the first coin is not taken out
bag[coin - 1] = 1
# Newly added state , because 1 Is the least significant value , So directly cover
for tar in range(amount - coin):
# Enumerative tar Satisfy : tar < amount - coin, namely tar + coin < amount
bag[tar + coin] = min(bag[tar + coin], bag[tar] + 1)
# Add coins to the current status , Transfer out
else:
# When the first coin is taken out
for mul, tar in enumerate(range(coin - 1, amount, coin)):
bag[tar] = mul + 1
# Initialization only considers the state of the first coin
return bag[-1]

Next, consider three scenarios ：

1. coins It's an empty list ： The target value cannot be reached without coins , So go back to -1. But follow the code —— Unable to enter for loop ,bag[-1] = inf, The return value is inf, So in return We have to judge before bag[-1] Is it not equal to inf
2. amount by 0：amount by 0, be bag It's an empty list , Will be in return It's a mistake
3. coins There is a face value greater than amount Of ：bag[coin - 1] = 1 List length exceeded , Will report a mistake

Modify for these three situations , The correct code is as follows ：

class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
if amount:
inf = amount + 1
bag = [inf for _ in range(amount)]
# bag Not empty condition : amount Not for 0
for idx, coin in enumerate(coins):
# No coin will go into circulation
if idx:
# When the first coin is not taken out
if coin <= amount:
bag[coin - 1] = 1
# Newly added state , because 1 Is the least significant value , So directly cover
for tar in range(amount - coin):
# Enumerative tar Satisfy : tar < amount - coin, namely tar + coin < amount
bag[tar + coin] = min(bag[tar + coin], bag[tar] + 1)
# Add coins to the current status , Transfer out
else:
# When the first coin is taken out
for mul, tar in enumerate(range(coin - 1, amount, coin)):
bag[tar] = mul + 1
# Initialization only considers the state of the first coin
result = bag[-1]
if result <= amount:
return result
# The result is not inf
else:
return -1
# The result is inf
else:
return 0
# The target value is 0, No coins required 

The test results are very good , end