這篇文章只有一些代碼,分析的內容很多,但是沒有進行必要的解釋
我也是第一次做,不是很懂股票,可能有一些錯誤。
# 導包
import numpy as np
import matplotlib.pyplot as plt
from pandas_datareader import data
from scipy.signal import find_peaks
from scipy.stats import norm
import pandas_datareader.data as web
import pandas_datareader.data as webdata
import datetime
import pandas as pd
import seaborn as sns # pip install seaborn
import matplotlib.patches as mpatches
from pyfinance import TSeries # pip install pyfinance
from empyrical import sharpe_ratio,omega_ratio,alpha_beta,stats # pip install empyrical
import warnings
warnings.filterwarnings('ignore')
tickers = ['F','TSLA','FSR','GM','NEE','SO','BYD','NIO','SOL','JKS']
startDate = '2019-06-01'
endDate = '2022-06-01'
F = webdata.get_data_stooq('F',startDate,endDate) # 福特
TSLA = webdata.get_data_stooq('TSLA',startDate,endDate) # 特斯拉
FSR = webdata.get_data_stooq('FSR',startDate,endDate) # 杜克能源公司
GM = webdata.get_data_stooq('GM',startDate,endDate) # 通用汽車
NEE = webdata.get_data_stooq('NEE',startDate,endDate) # NextEra能源公司
SO = webdata.get_data_stooq('SO',startDate,endDate)# 南方公司
BYD = webdata.get_data_stooq('BYD',startDate,endDate)# 比亞迪
NIO = webdata.get_data_stooq('NIO',startDate,endDate) # 蔚來
SOL = webdata.get_data_stooq('SOL',startDate,endDate) # 瑞能新能源
JKS = webdata.get_data_stooq('JKS',startDate,endDate) # 法拉第未來
stocks = pd.DataFrame({
"F": F["Close"],
"TSLA": TSLA["Close"],
"FSR": FSR["Close"],
"GM": GM["Close"],
"NEE": NEE["Close"],
"SO": SO["Close"],
"BYD": BYD["Close"],
"NIO": NIO["Close"],
"SOL": SOL["Close"],
"JKS": JKS["Close"],
})
stocks
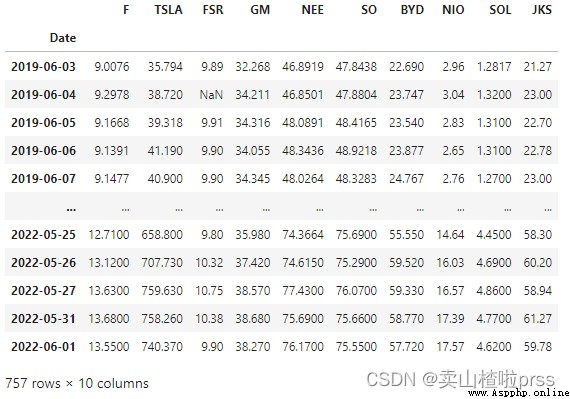
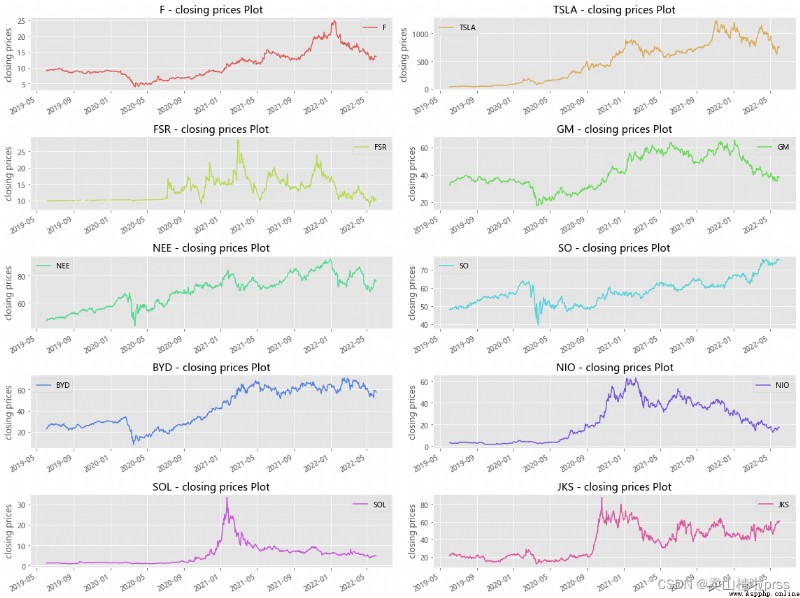
Plot the closing prices of the stocks
# 收盤價走勢
plt.style.use('ggplot') # 樣式
color_palette=sns.color_palette("hls",10) # 顏色
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (16,12))
for i,j in enumerate(tickers):
plt.subplot(5,2,i+1)
stocks[j].plot(kind='line', style=['-'],color=color_palette[i],label=j)
plt.xlabel('')
plt.ylabel('closing prices')
plt.title('{} - closing prices Plot'.format(j))
plt.legend()
plt.tight_layout()
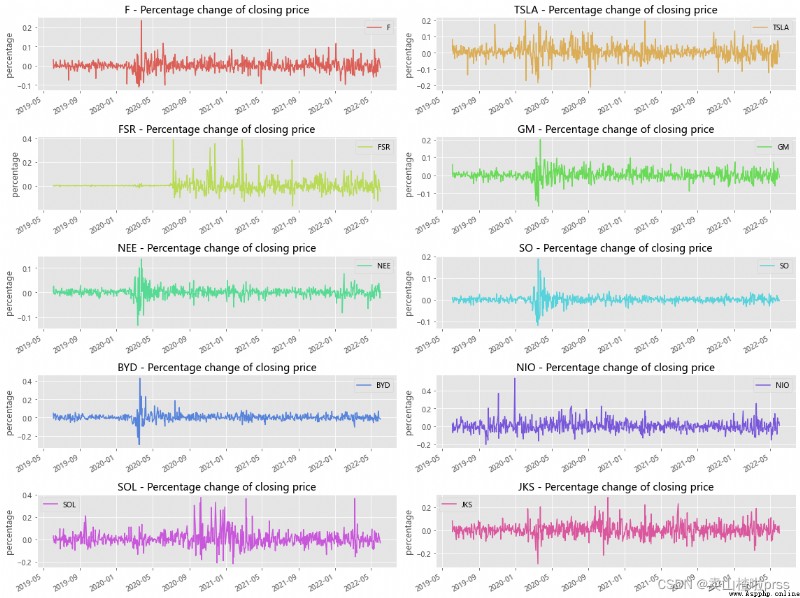
Percentage change of closing price(day)
# 每日的收益率走勢
# 通過上圖可以看到,整體呈上下波動趨勢,個別時間點波動性較大。
plt.style.use('ggplot')
color_palette=sns.color_palette("hls",10)
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (16,12))
for i,j in enumerate(tickers):
plt.subplot(5,2,i+1)
stocks[j].pct_change().plot(kind='line', style=['-'],color=color_palette[i],label=j)
plt.xlabel('')
plt.ylabel('percentage')
plt.title('{} - Percentage change of closing price'.format(j))
plt.legend()
plt.tight_layout()
Average daily return of closing price
# 日平均收益
for i in tickers:
r_daily_mean = ((1+stocks[i].pct_change()).prod())**(1/stocks[i].shape[0])-1
#print("%s - Average daily return:%f"%(i,r_daily_mean))
print("%s - Average daily return is:%s"%(i,str(round(r_daily_mean*100,2))+"%"))
F - Average daily return is:0.05%
TSLA - Average daily return is:0.4%
FSR - Average daily return is:0.0%
GM - Average daily return is:0.02%
NEE - Average daily return is:0.06%
SO - Average daily return is:0.06%
BYD - Average daily return is:0.12%
NIO - Average daily return is:0.24%
SOL - Average daily return is:0.17%
JKS - Average daily return is:0.14%
# 日收益率的概率分布圖
# 查看分布情況
plt.style.use('ggplot')
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (16,12))
for i,j in enumerate(tickers):
plt.subplot(5,2,i+1)
sns.distplot(stocks[j].pct_change(), bins=100, color=color_palette[i])
plt.ylabel('Daily Return')
plt.title('{} - Daily Return distribution'.format(j))
plt.tight_layout();
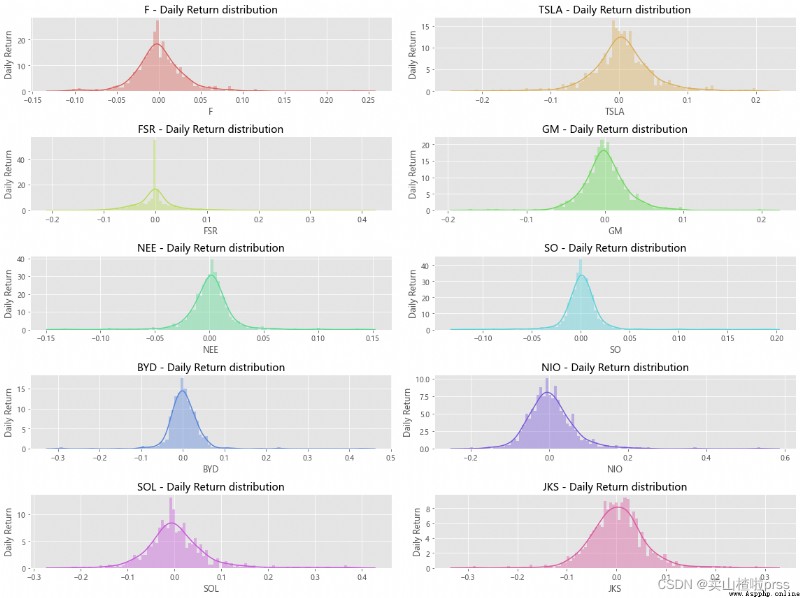
# 累積日收益率
# 累積日收益率有助於定期確定投資價值。可以使用每日百分比變化的數值來計算累積日收益率,只需將其加上1並計算累積的乘積。
# 累積日收益率是相對於投資計算的。如果累積日收益率超過1,就是在盈利,否則就是虧損。
plt.style.use('ggplot')
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (16,12))
for i,j in enumerate(tickers):
plt.subplot(5,2,i+1)
cc = (1+stocks[j].pct_change()).cumprod()
cc.plot(kind='line', style=['-'],color=color_palette[i],label=j)
plt.xlabel('')
plt.title('{} - Cumulative daily return'.format(j))
plt.legend()
plt.tight_layout()
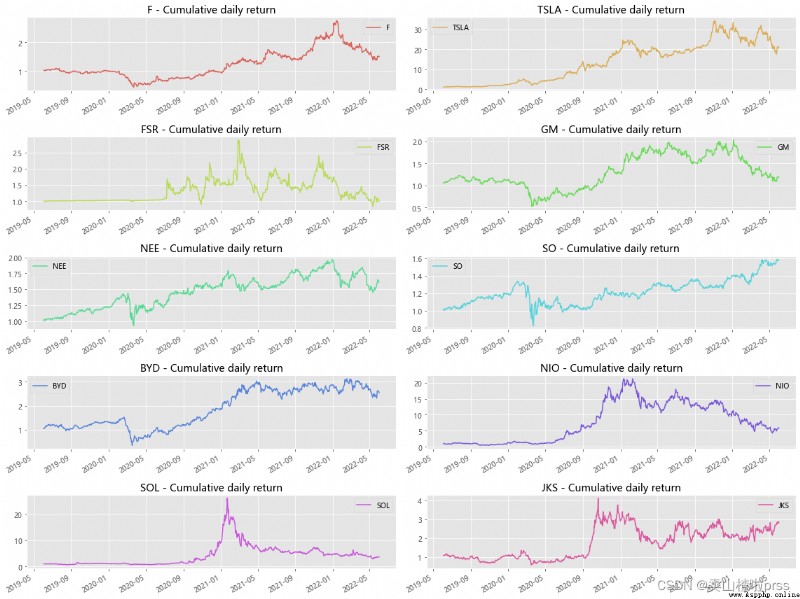
Monthly return of closing price
# 月收益率
# 對月收益率進行可視化分析,標注收益率高於四分之三分位數的點。
# 月收益率圍繞均線上下波動
fig = plt.figure(figsize = (16,12))
for i,j in enumerate(tickers):
plt.subplot(5,2,i+1)
daily_ret = stocks[j].pct_change()
mnthly_ret = daily_ret.resample('M').apply(lambda x : ((1+x).prod()-1))
mnthly_ret.plot(color=color_palette[i]) # Monthly return
start_date=mnthly_ret.index[0]
end_date=mnthly_ret.index[-1]
plt.xticks(pd.date_range(start_date,end_date,freq='Y'),[str(y) for y in range(start_date.year+1,end_date.year+1)])
# Show points with monthly yield greater than 3/4 quantile
dates=mnthly_ret[mnthly_ret>mnthly_ret.quantile(0.75)].index
for i in range(0,len(dates)):
plt.scatter(dates[i], mnthly_ret[dates[i]],color='r')
labs = mpatches.Patch(color='red',alpha=.5, label="Monthly return higher than 3/4")
plt.title('%s - Monthly return of closing price'%j,size=15)
plt.legend(handles=[labs])
plt.tight_layout()
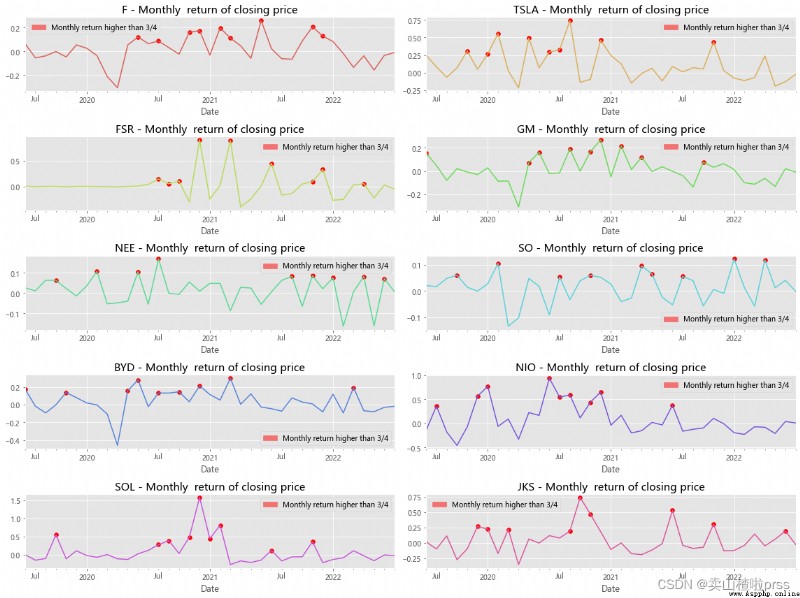
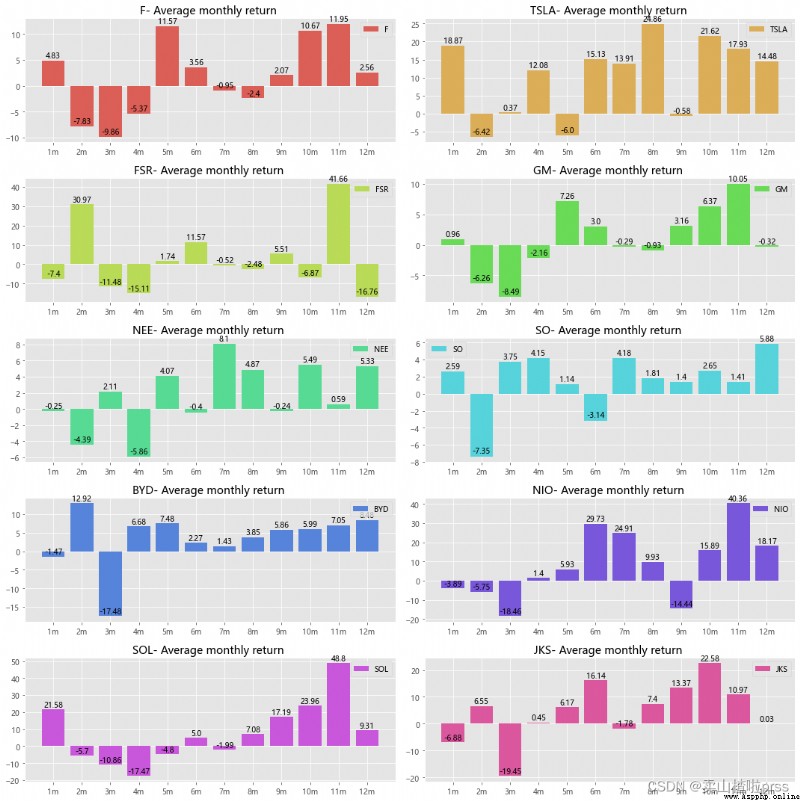
Average monthly return
# 月平均收益
plt.style.use('ggplot')
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (15,15))
for i,j in enumerate(tickers):
plt.subplot(5,2,i+1)
daily_ret = stocks[j].pct_change()
mnthly_ret = daily_ret.resample('M').apply(lambda x : ((1+x).prod()-1))
mrets=(mnthly_ret.groupby(mnthly_ret.index.month).mean()*100).round(2)
attr=[str(i)+'m' for i in range(1,13)]
v=list(mrets)
plt.bar(attr, v,color=color_palette[i],label=j)
for a, b in enumerate(v):
plt.text(a, b+0.08,b,ha='center',va='bottom')
plt.title('{}- Average monthly return '.format(j))
plt.legend()
plt.tight_layout()
# 圖中顯示某些月份具有正的收益率均值,而某些月份具有負的收益率均值,
Three year compound annual growth rate (CAGR)
復合年增長率(Compound Annual Growth Rate,CAGR)是一項投資在特定時期內的年度增長率
CAGR=(現有價值/基礎價值)^(1/年數) - 1 或 (end/start)^(1/# years)-1
它是一段時間內的恆定回報率。換言之,該比率告訴你在投資期結束時,你真正獲得的收益。它的目的是描述一個投資回報率轉變成一個較穩定的投資回報所得到的預想值。
# 復合年增長率(CAGR)
for i in tickers:
days = (stocks[i].index[0] - stocks[i].index[-1]).days
CAGR_3 = (stocks[i][-1]/ stocks[i][0])** (365.0/days) - 1
print("%s (CAGR):%s"%(i,str(round(CAGR_3*100,2))+"%"))
F (CAGR):-12.74%
TSLA (CAGR):-63.6%
FSR (CAGR):-0.03%
GM (CAGR):-5.53%
NEE (CAGR):-14.94%
SO (CAGR):-14.14%
BYD (CAGR):-26.77%
NIO (CAGR):-44.8%
SOL (CAGR):-34.81%
JKS (CAGR):-29.16%
Annualized rate of return
# 年化收益率
# 年化收益率,是判斷一只股票是否具備投資價值的重要標准!
# 年化收益率,即每年每股分紅除以股價
for i in tickers:
r_daily_mean = ((1+stocks[i].pct_change()).prod())**(1/stocks[i].shape[0])-1
annual_rets = (1+r_daily_mean)**252-1
print("%s'annualized rate of return is:%s"%(i,str(round(annual_rets*100,2))+"%"))
F’annualized rate of return is:14.56%
TSLA’annualized rate of return is:174.14%
FSR’annualized rate of return is:0.03%
GM’annualized rate of return is:5.84%
NEE’annualized rate of return is:17.53%
SO’annualized rate of return is:16.43%
BYD’annualized rate of return is:36.45%
NIO’annualized rate of return is:80.92%
SOL’annualized rate of return is:53.24%
JKS’annualized rate of return is:41.06%
maximum drawdowns
最大回撤率(Maximum Drawdown),它用於測量在投資組合價值中,在下一次峰值來到之前,最高點和最低點之間的最大單次下降。換言之,該值代表了基於某個策略的投資組合風險。
“最大回撤率是指在選定周期內任一歷史時點往後推,產品淨值走到最低點時的收益率回撤幅度的最大值。最大回撤用來描述買入產品後可能出現的最糟糕的情況。最大回撤是一個重要的風險指標,對於對沖基金和數量化策略交易,該指標比波動率還重要。”
最大回撤率超過了自己的風險承受范圍,建議謹慎選擇。
# 最大回撤率
def getMaxDrawdown(x):
j = np.argmax((np.maximum.accumulate(x) - x) / x)
if j == 0:
return 0
i = np.argmax(x[:j])
d = (x[i] - x[j]) / x[i] * 100
return d
for i in tickers:
MaxDrawdown = getMaxDrawdown(stocks[i])
print("%s maximum drawdowns:%s"%(i,str(round(MaxDrawdown,2))+"%"))
F maximum drawdowns:59.97%
TSLA maximum drawdowns:60.63%
FSR maximum drawdowns:0%
GM maximum drawdowns:57.53%
NEE maximum drawdowns:35.63%
SO maximum drawdowns:38.43%
BYD maximum drawdowns:77.43%
NIO maximum drawdowns:79.77%
SOL maximum drawdowns:88.88%
JKS maximum drawdowns:65.44%
calmer ratios for the top performers
# calmar率
# Calmar比率(Calmar Ratio) 描述的是收益和最大回撤之間的關系。計算方式為年化收益率與歷史最大回撤之間的比率。
# Calmar比率數值越大,股票表現越好。
def performance(i):
a = stocks[i].pct_change()
s = a.values
idx = a.index
tss = TSeries(s, index=idx)
dd={
}
dd['anlzd_ret']=str(round(tss.anlzd_ret()*100,2))+"%"
dd['cuml_ret']=str(round(tss.cuml_ret()*100,2))+"%"
dd['max_drawdown']=str(round(tss.max_drawdown()*100,2))+"%"
dd['sortino_ratio']=str(round(tss.sortino_ratio(freq=250),2))+"%"
dd['calmar_ratio']=str(round(tss.calmar_ratio()*100,2))+"%"
dd['sharpe_ratio'] = str(round(sharpe_ratio(tss)*100,2))+"%" # 夏普比率(Sharpe Ratio):風險調整後的收益率.計算投資組合每承受一單位總風險,會產生多少的超額報酬。
dd['annual_volatility'] = str(round(stats.annual_volatility(tss)*100,2))+"%" # 波動率
dd['omega_ratio'] = str(round(omega_ratio(tss)*100,2))+"%" # omega_ratio
df=pd.DataFrame(dd.values(),index=dd.keys(),columns = [i])
return df
dff = pd.DataFrame()
for i in tickers:
dd = performance(i)
dff = pd.concat([dff,dd],axis=1)
dff
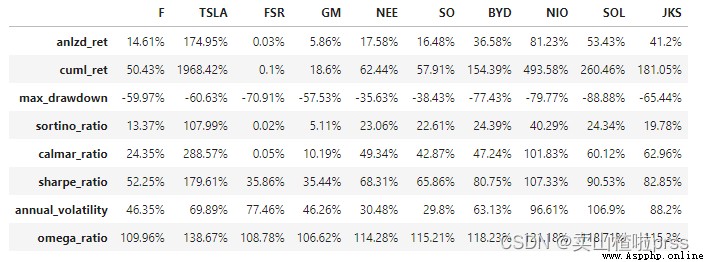
Volatility
# 日收益率的年度波動率(滾動)
fig = plt.figure(figsize = (16,15))
for ii,jj in enumerate(tickers):
plt.subplot(5,2,ii+1)
vol = stocks[jj].pct_change()[::-1].rolling(window=252,center=False).std()* np.sqrt(252)
plt.plot(vol,color=color_palette[ii],label=jj)
plt.legend()
plt.tight_layout()
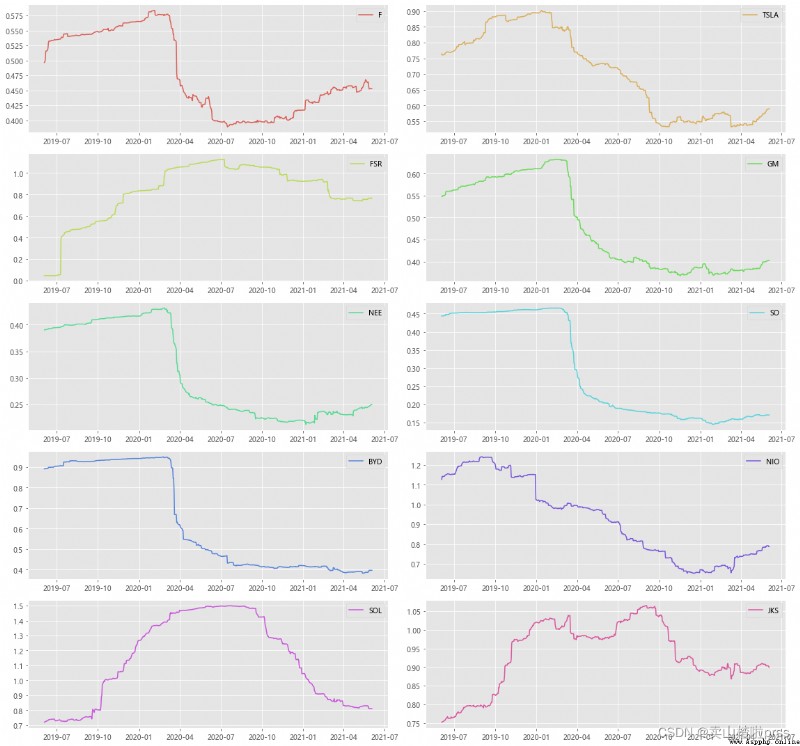
# Annualized standard deviation (volatility) of monthly return
# 月收益率的年化標准差(波動率)
# 實證研究表明,收益率標准差(波動率)存在一定的集聚現象,
# 即高波動率和低波動率往往會各自聚集在一起,並且高波動率和低波動率聚集的時期是交替出現的。
# 紅色部門顯示出,所有股票均存在一定的波動集聚現象。
fig = plt.figure(figsize = (16,15))
for ii,jj in enumerate(tickers):
plt.subplot(5,2,ii+1)
daily_ret=stocks[jj].pct_change()
mnthly_annu = daily_ret.resample('M').std()* np.sqrt(12)
#plt.rcParams['figure.figsize']=[20,5]
mnthly_annu.plot(color=color_palette[ii],label=jj)
start_date=mnthly_annu.index[0]
end_date=mnthly_annu.index[-1]
plt.xticks(pd.date_range(start_date,end_date,freq='Y'),[str(y) for y in range(start_date.year+1,end_date.year+1)])
dates=mnthly_annu[mnthly_annu>0.07].index
for i in range(0,len(dates)-1,3):
plt.axvspan(dates[i],dates[i+1],color=color_palette[ii],alpha=.3)
plt.title('%s - Standard deviation of monthly rate of return'%jj,size=15)
labs = mpatches.Patch(color=color_palette[ii],alpha=.5, label="Volatility agglomeration")
plt.legend(handles=[labs])
plt.tight_layout()
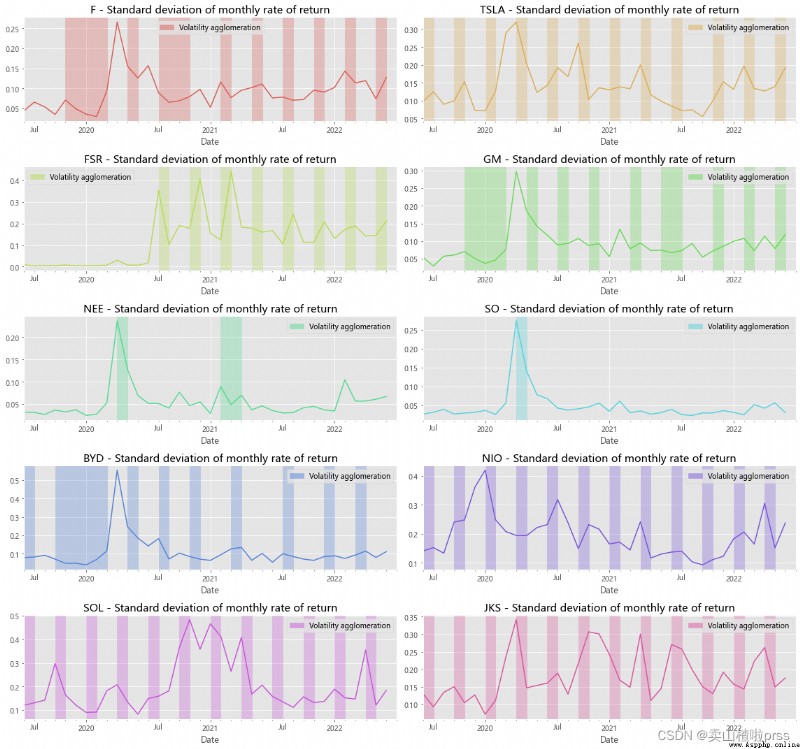
Pairs Trading
# 配對策略
# Analysis object:BYD&GM
# Comparison of closing price line chart
ax1 = BYD.plot(y='Close',label='BYD',figsize=(16,8))
GM.plot(ax=ax1,y='Close',label='GM')
plt.title('Closing price comparison')
plt.xlabel('Date')
plt.ylabel('Close')
plt.grid(True)
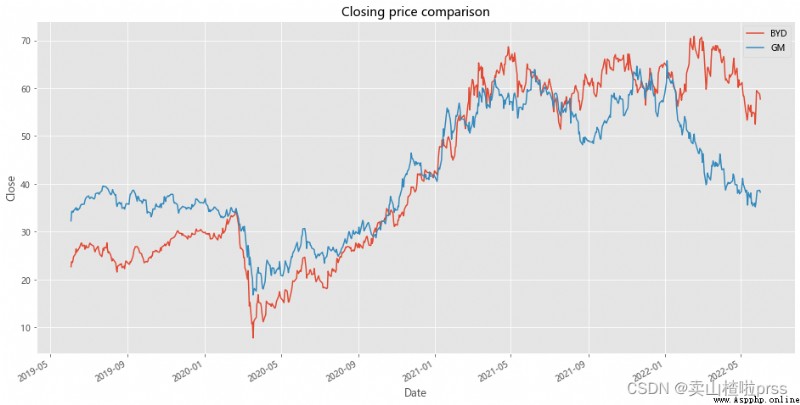
# Price difference and its mean value
# 收盤價價差及其均值
BYD['diff'] =BYD['Close']-GM['Close']
BYD['diff'].plot(figsize=(16,10))
plt.title('Price difference between BYD and GM')
plt.xlabel('Dtae')
plt.ylabel('Price difference')
plt.axhline(BYD['diff'].mean(),color='blue')
plt.grid(True)
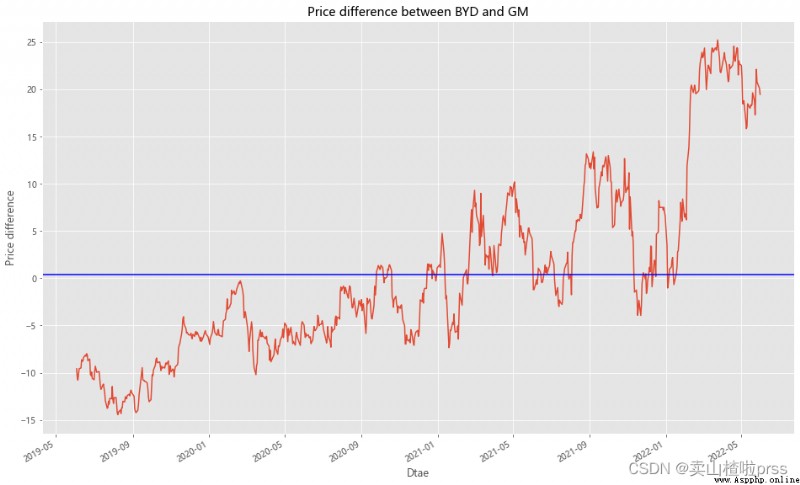
# Maximum deviation point
# 最大收盤價差值
BYD['diff'][BYD['diff']==max(BYD['diff'])]
Date
2022-03-25 25.214
Name: diff, dtype: float64
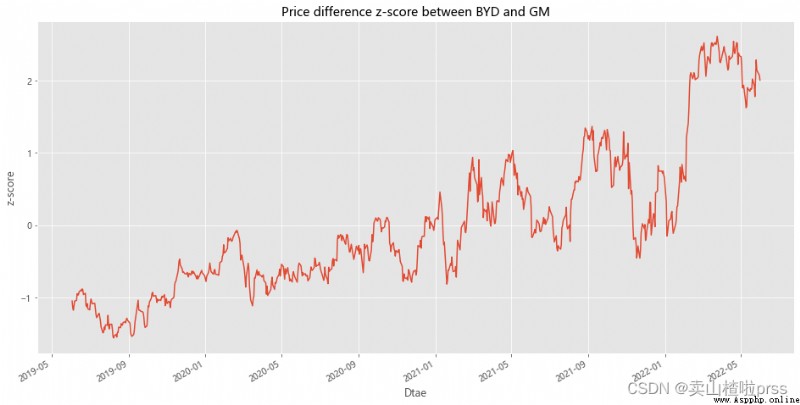
# Measure how far the series deviates from the mean
# 測量BYD和GM兩只股票收盤價差值 偏離平均值的程度
# 對價差進行標准化
BYD['zscore'] =(BYD['diff']-np.mean(BYD['diff']))/np.std(BYD['diff'])
BYD['zscore'].plot(figsize=(16,8))
plt.title('Price difference z-score between BYD and GM')
plt.xlabel('Dtae')
plt.ylabel('z-score')
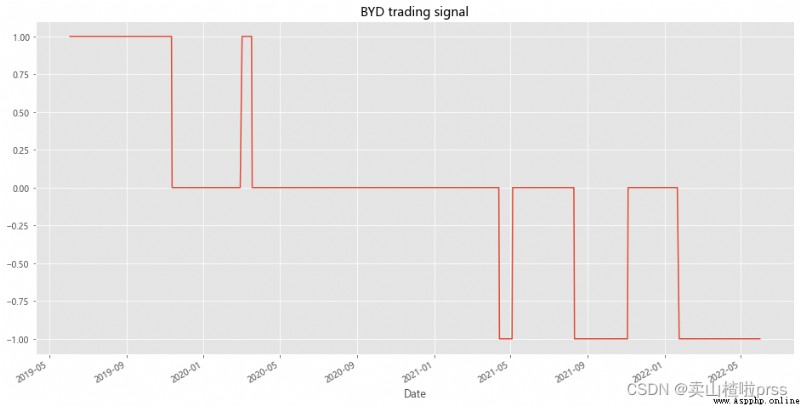
# BYD trading signal
# BYD 股票買賣交易信號
BYD['position1'] = np.where(BYD['zscore']>1,-1,np.nan) # Greater than 1, long
BYD['position1'] = np.where(BYD['zscore']<-1,1,BYD['position1']) # Less than -1, short
BYD['position1'] = np.where(abs(BYD['zscore'])<0.5,0,BYD['position1']) # Close positions within 0.5 range
BYD['position1'] = BYD['position1'].ffill().fillna(0)
BYD['position1'].plot(ylim=[-1.1,1.1],title='BYD trading signal',xlabel='Date',figsize=(16,8))
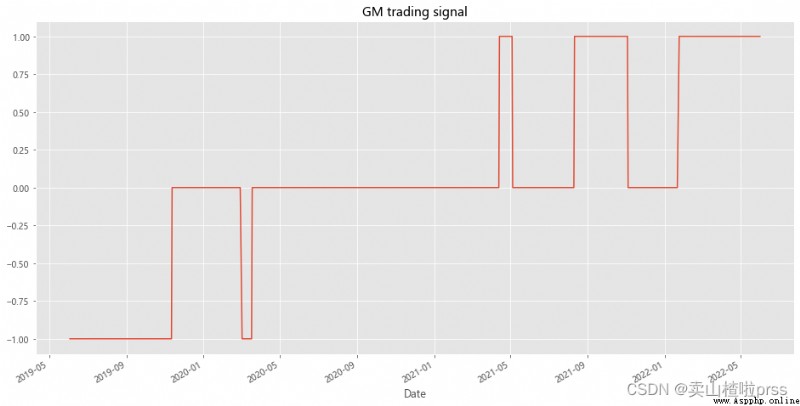
# GM trading signal
# GM 股票買賣交易信號
BYD['position2'] = -np.sign(BYD['position1']) # Opposite to BYD
BYD['position2'].plot(ylim=[-1.1,1.1],title='GM trading signal',xlabel='Date',figsize=(16,8))
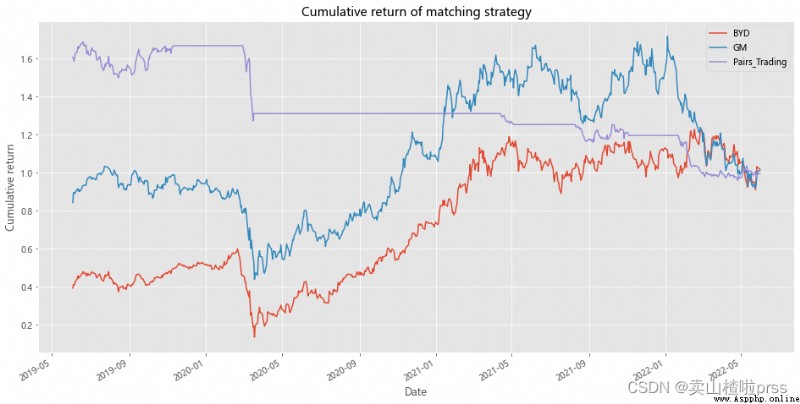
# Cumulative return of strategy
# 配對策略累計收益率
BYD['BYD']=(np.log(BYD['Close']/BYD['Close'].shift(1))).fillna(0)
BYD['GM']=(np.log(GM['Close']/GM['Close'].shift(1))).fillna(0)
BYD['Pairs_Trading']=0.5*(BYD['position1'].shift(1)*BYD['BYD'])+0.5*(BYD['position2'].shift(1)*BYD['GM'])
BYD[['BYD','GM','Pairs_Trading']].dropna().cumsum().apply(np.exp).plot(figsize=(16,8))
plt.title('Cumulative return of matching strategy')
plt.xlabel('Date')
plt.ylabel('Cumulative return')
plt.grid(True)
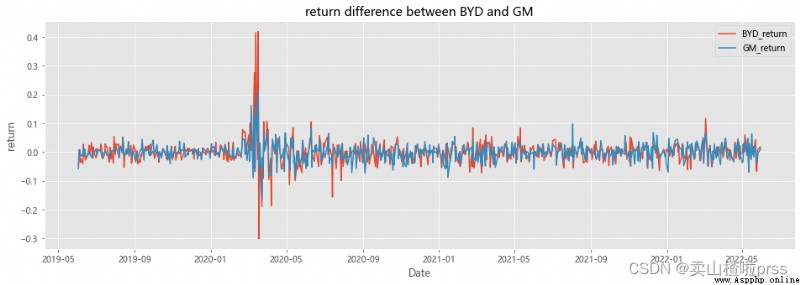
漲跌幅分析
BYD_return = BYD['Close'].pct_change()
GM_return = GM['Close'].pct_change()
BYD['diff_return'] = BYD_return - GM_return
cr = BYD['diff_return'][BYD['diff_return']==BYD['diff_return'].max()]
print('最大收益率差',cr.values[0])
# 最大收益率差 0.2384556461576477
fig = plt.figure(figsize = (16,5))
plt.plot(BYD_return.index,BYD_return,label='BYD_return')
plt.plot(GM_return.index,GM_return,label='GM_return')
plt.title('return difference between BYD and GM')
plt.xlabel('Date')
plt.ylabel('return')
plt.legend()
plt.grid(True)
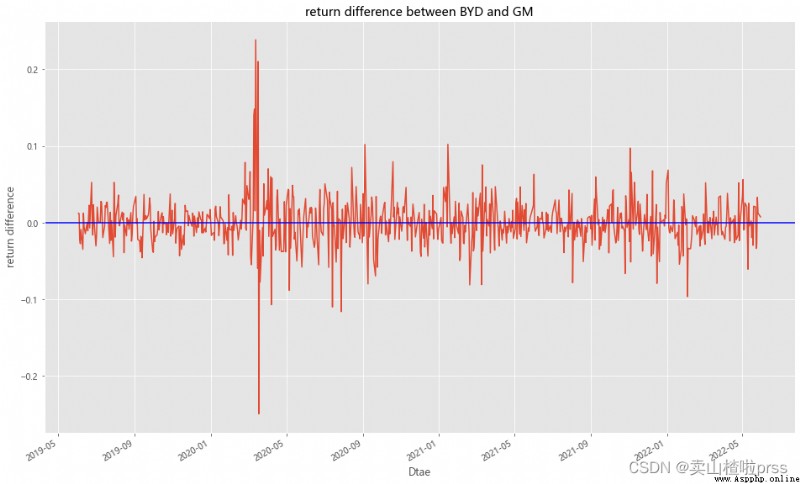
# 漲跌幅差異
BYD['diff_updown'] =BYD_return-GM_return
BYD['diff_updown'].plot(figsize=(16,10))
plt.title('return difference between BYD and GM')
plt.xlabel('Dtae')
plt.ylabel('return difference')
plt.axhline(BYD['diff_updown'].mean(),color='blue')
plt.grid(True)
# 累計漲跌幅
def profit(closeCol):
try:
p=(closeCol.iloc[-1]-closeCol.iloc[0])/closeCol.iloc[0]*100.00
except Exception:
return None
return round(p,2)
for i in ['BYD','GM']:
closeCol=stocks1[i] # 獲取收盤價Close這一列的數據
babaChange=profit(closeCol)# 調用函數,獲取漲跌幅
print(i,str(babaChange)+'%')
BYD 154.39%
GM 18.6%
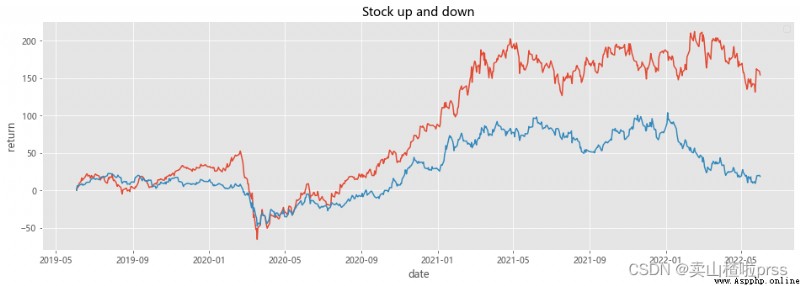
# Analysis of stock fluctuation
# 定基漲幅變化對比
def show(stocks, axs=None):
n = []
drawer = plt if axs is None else axs
for i in stocks.columns:
drawer.plot(100*(stocks[i]/stocks[i].iloc[0]-1)) # 歸一化處理
drawer.grid(True)
drawer.legend(n, loc='best')
plt.figure(figsize = (16,5))
show(stocks[['BYD','GM']])
plt.title('Stock up and down')
plt.xlabel('date')
plt.ylabel('return')
plt.show()
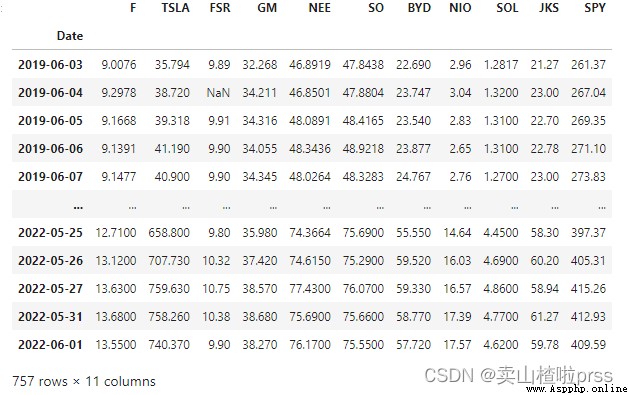
Compare them against two major indices like the S&P 500
# 標准普爾500指數 作比較
SPY = webdata.get_data_stooq('SPY',startDate,endDate)
stocks1 = pd.concat([stocks,SPY['Close']],axis=1)
stocks1.columns = ['F','TSLA','FSR','GM','NEE','SO','BYD','NIO','SOL','JKS','SPY']
stocks1
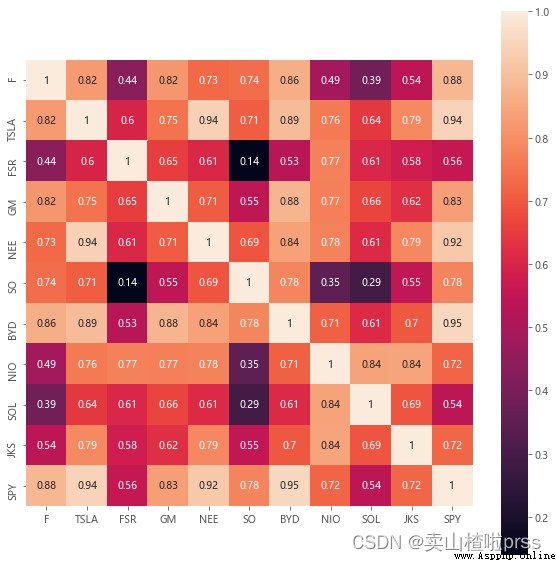
# 相關性矩陣
# SPY與其他股票(價格)相關性——最後一排
plt.figure(figsize = (10,10))
sns.heatmap(stocks1.corr(), annot=True, vmax=1, square=True) # 繪制df_corr的矩陣熱力圖
plt.show() # 顯示圖片
benchmark = TSeries(SPY['Close'].pct_change()[::-1])
dd={
}
dd['anlzd_ret']=str(round(benchmark.anlzd_ret()*100,2))+"%"
dd['cuml_ret']=str(round(benchmark.cuml_ret()*100,2))+"%"
dd['max_drawdown']=str(round(benchmark.max_drawdown()*100,2))+"%"
dd['sortino_ratio']=str(round(benchmark.sortino_ratio(freq=250),2))+"%"
dd['calmar_ratio']=str(round(benchmark.calmar_ratio()*100,2))+"%"
dd['sharpe_ratio'] = str(round(sharpe_ratio(benchmark)*100,2))+"%" # 夏普比率(Sharpe Ratio):風險調整後的收益率.計算投資組合每承受一單位總風險,會產生多少的超額報酬。
dd['annual_volatility'] = str(round(stats.annual_volatility(benchmark)*100,2))+"%" # 波動率
dd['omega_ratio'] = str(round(omega_ratio(benchmark)*100,2))+"%" # omega_ratio
df_benchmark =pd.DataFrame(dd.values(),index=dd.keys(),columns = ['SPY'])
df_benchmark
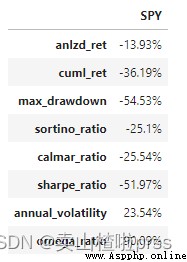
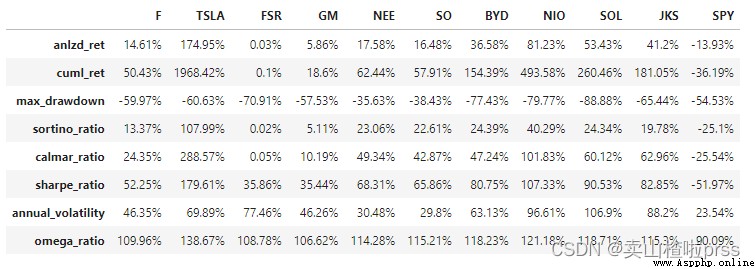
dff = pd.concat([dff,df_benchmark],axis=1)
dff
# 可對比每只股票的年化收益、累計收益、最大回撤率、索提諾比率(投資組合的向下波動率,)、calmar率等
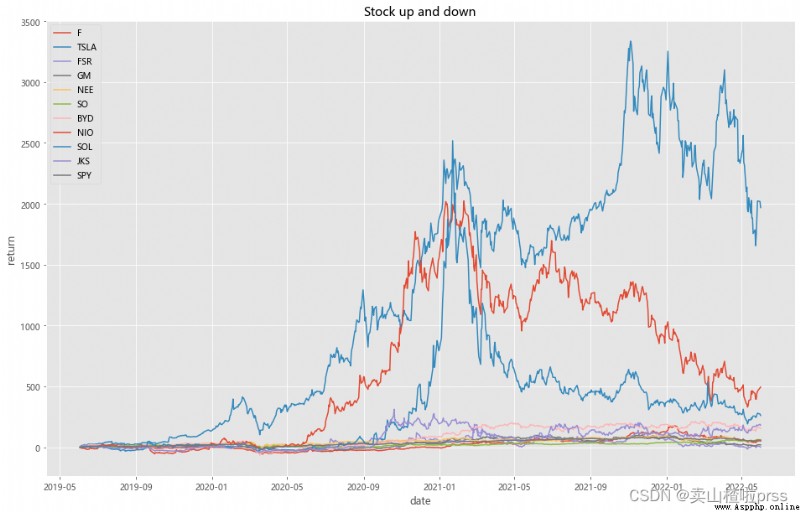
# Analysis of stock fluctuation
def show(stocks, axs=None):
n = []
drawer = plt if axs is None else axs
for i in stocks.columns:
if i != '日期':
n.append(i)
drawer.plot(100*(stocks[i]/stocks[i].iloc[0]-1)) # 歸一化處理
drawer.grid(True)
drawer.legend(n, loc='best')
plt.figure(figsize = (16,10))
show(stocks)
plt.title('Stock up and down')
plt.xlabel('date')
plt.ylabel('return')
plt.show()
# 計算股票漲跌幅=(現在股價-買入價格)/買入價格
def profit(closeCol):
try:
p=(closeCol.iloc[0]-closeCol.iloc[-1])/closeCol.iloc[-1]*100.00
except Exception:
return None
return round(p,2)
for i in tickers+['SPY']:
closeCol=stocks1[i] # 獲取收盤價Close這一列的數據
babaChange=profit(closeCol)# 調用函數,獲取漲跌幅
print(i,str(babaChange)+'%')
F -33.52%
TSLA -95.17%
FSR -0.1%
GM -15.68%
NEE -38.44%
SO -36.67%
BYD -60.69%
NIO -83.15%
SOL -72.26%
JKS -64.42%
SPY -36.19%
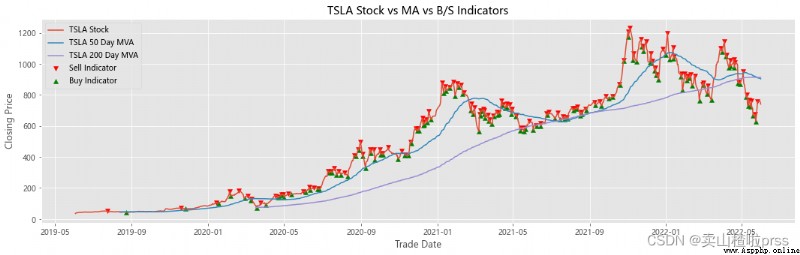
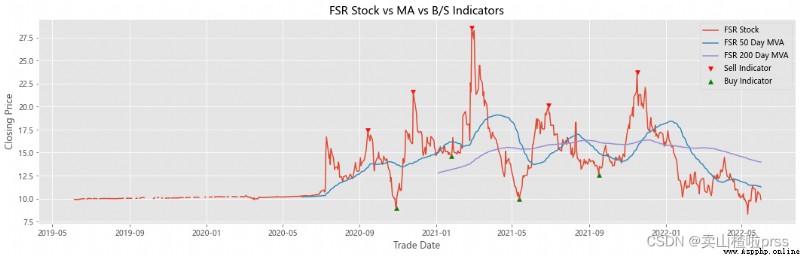
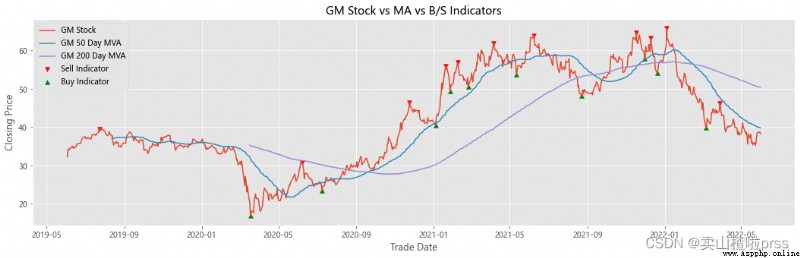
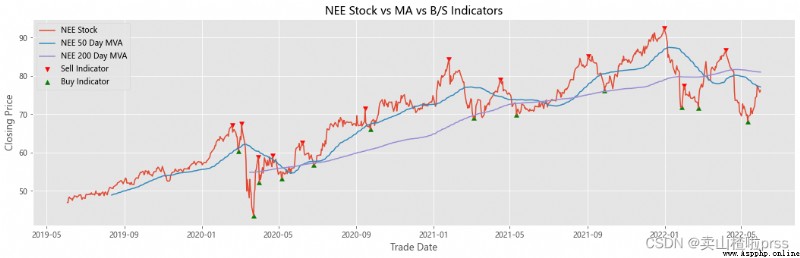
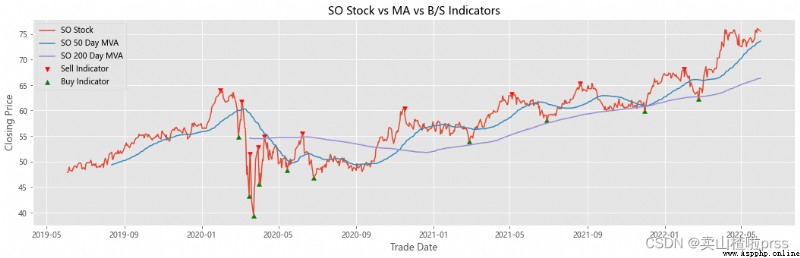
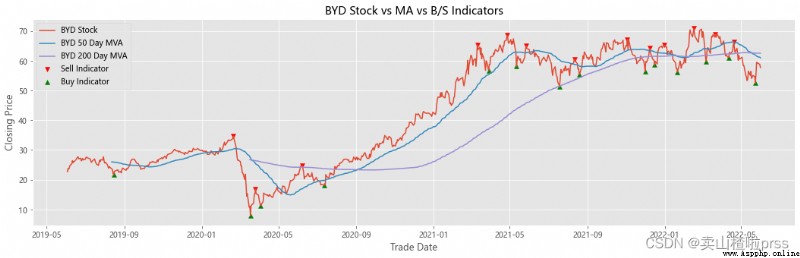
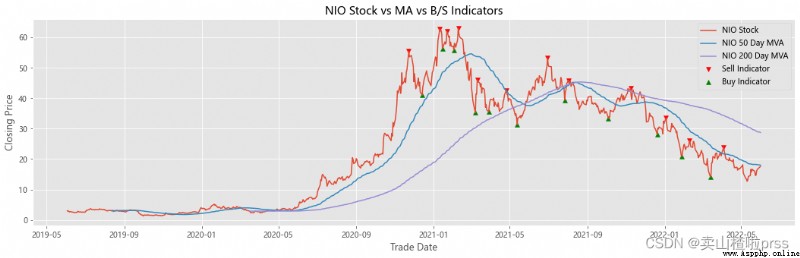
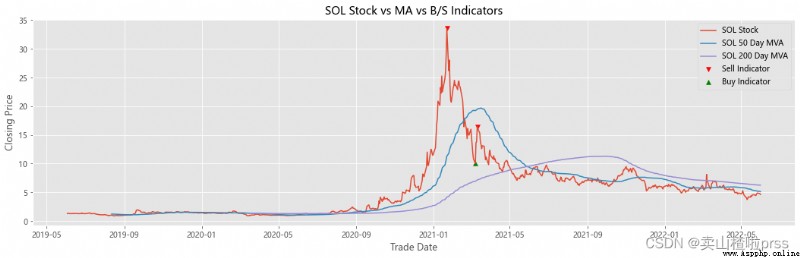
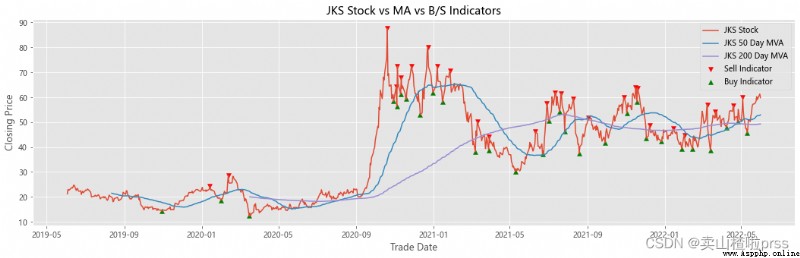
Add stocks, signals and moving averages to plot and visualize
# 股票、信號和移動平均線以繪制和可視化
# 查看股票平穩性
# 有些散戶喜歡利用移動平均線來判斷買入賣出,比如常見的,五日ma5上穿十日均線ma10時買入股票,反之賣出股票。
for i in tickers:
stock_close = stocks[i]
## Add stocks, signals and moving averages to plot and visualize
maximaIndex, _ = find_peaks(stock_close, prominence=5)
maxPrices = [stock_close[i] for i in maximaIndex]
minimaIndex, _ = find_peaks(stock_close * (-1), prominence=5)
minPrices = [stock_close[i] for i in minimaIndex]
fig, ax = plt.subplots(figsize = (18,5))
ax.scatter(stock_close.index[maximaIndex], maxPrices, marker='v', color='red', label='Sell Indicator')
ax.scatter(stock_close.index[minimaIndex], minPrices, marker='^', color='green', label='Buy Indicator')
ax.plot(stock_close.index, stock_close, label = '{} Stock'.format(i))
ax.set_xlabel('Trade Date')
ax.set_ylabel('Closing Price')
ax.set_title('{} Stock vs MA vs B/S Indicators'.format(i))
shortRollingMVA = stock_close.rolling(window=50).mean()
longRollingMVA = stock_close.rolling(window=200).mean()
ax.plot(shortRollingMVA.index, shortRollingMVA, label = '{} 50 Day MVA'.format(i))
ax.plot(longRollingMVA.index, longRollingMVA, label = '{} 200 Day MVA'.format(i))
ax.legend()

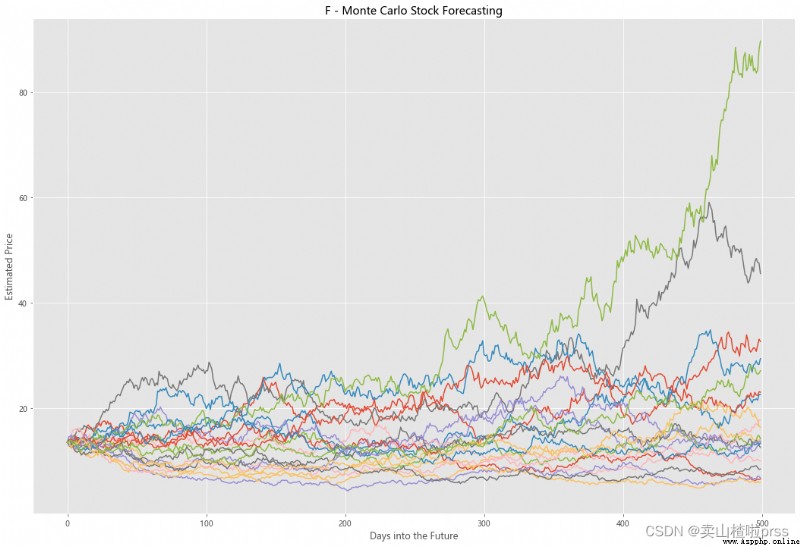
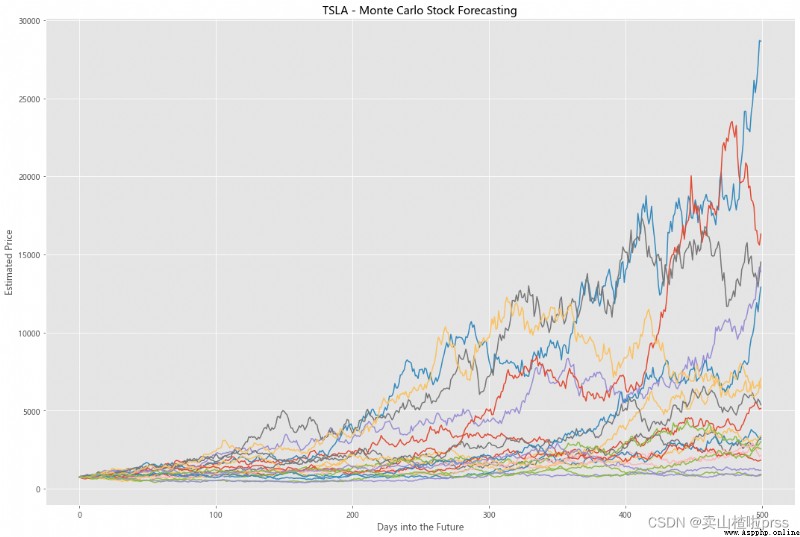
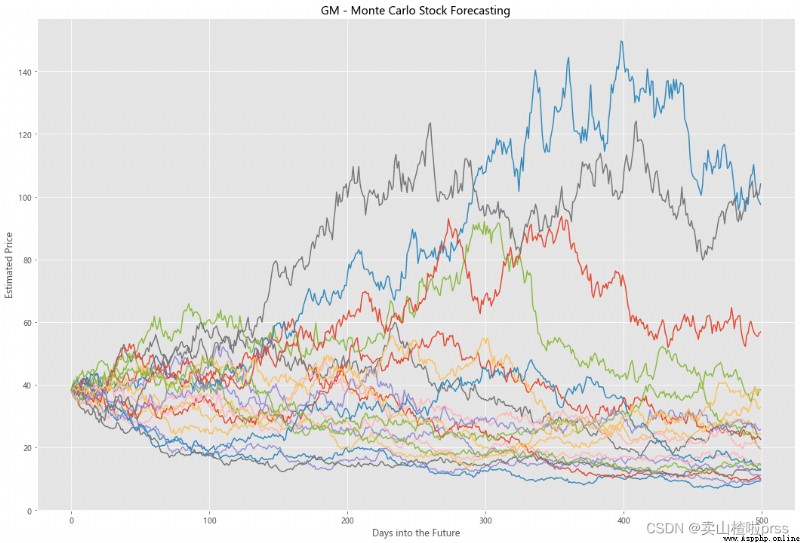
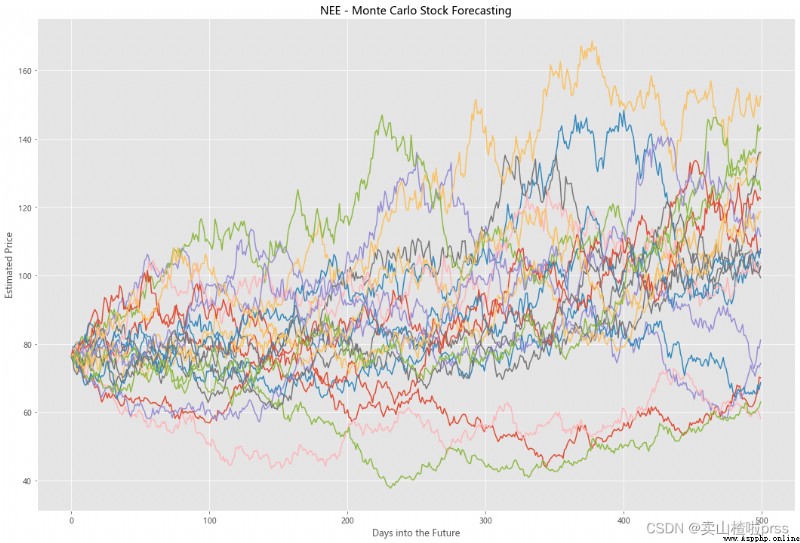
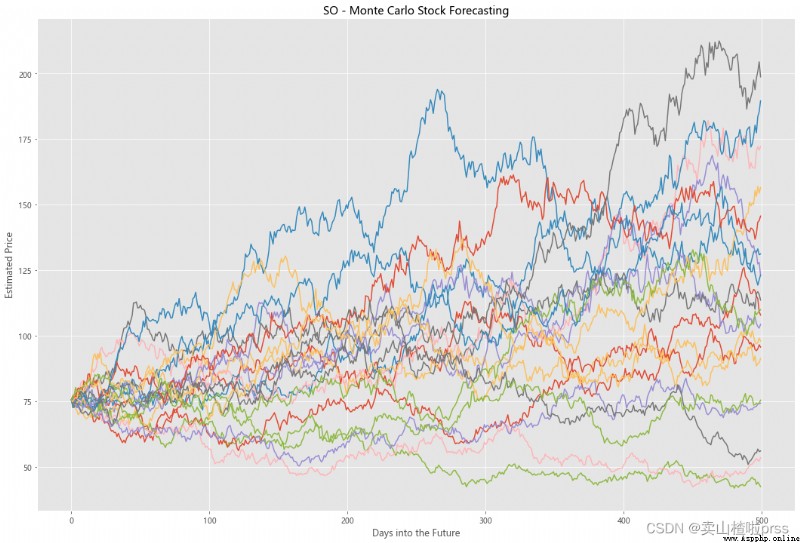
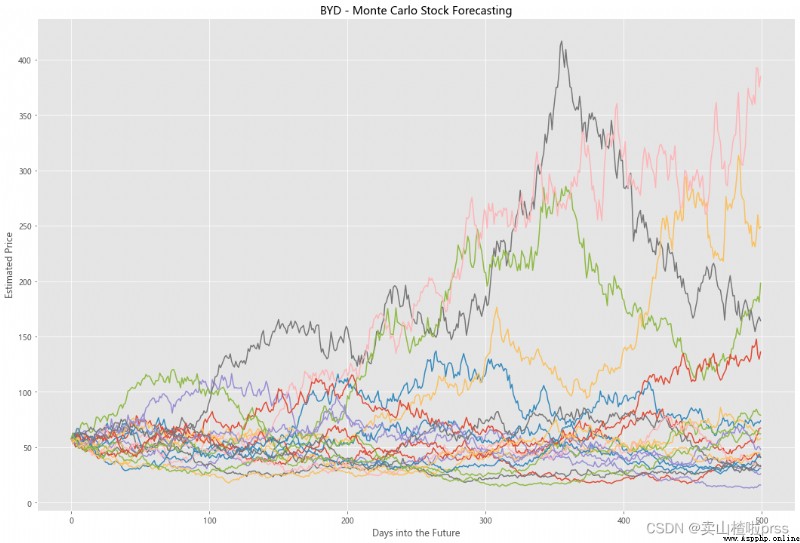
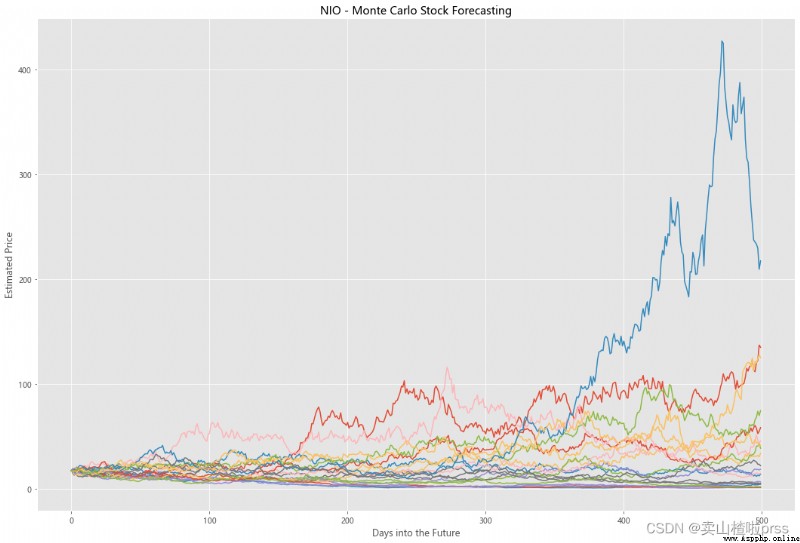
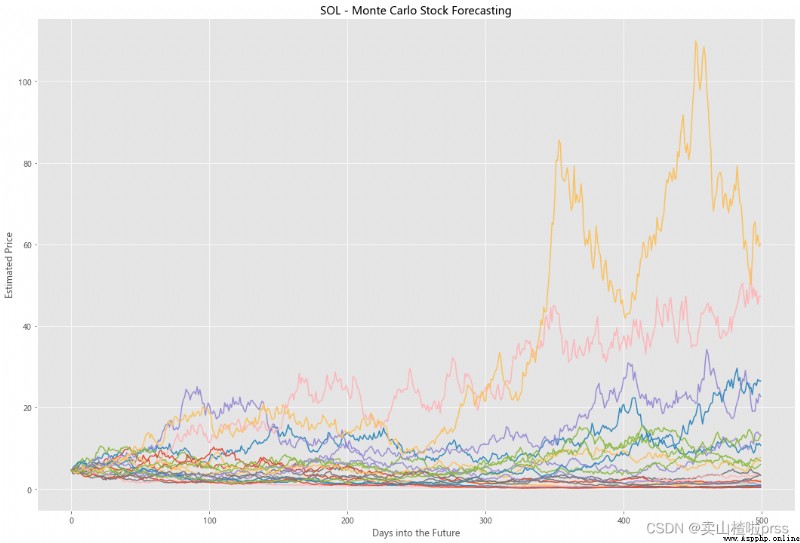
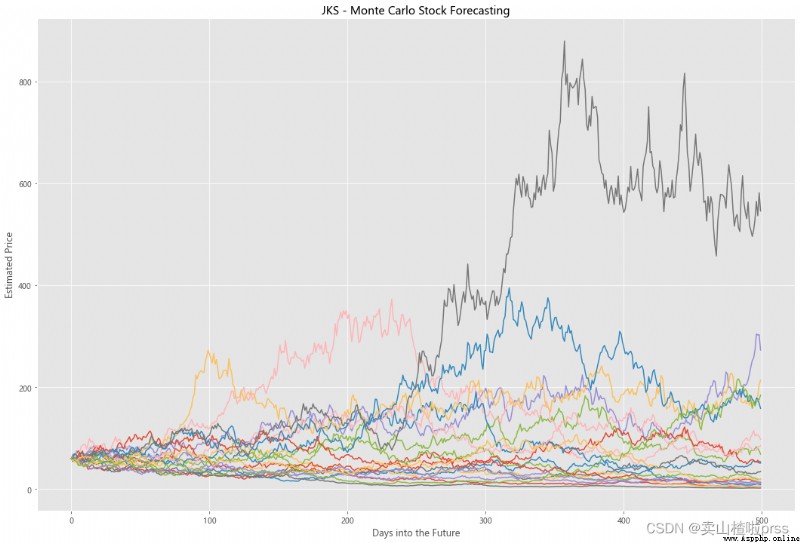
Try to forecast future stock movements via Monte Carlo Simulations
# 通過蒙特卡羅模擬預測未來的股票走勢
# 蒙特卡洛模擬是一種統計學方法,用來模擬數據的演變趨勢。
# 蒙特卡洛模擬其中20條模擬路徑圖
for i in tickers:
stock_close = stocks[i]
logReturns = np.log(1+stock_close.pct_change())
## Need mean and standard deviation to calculate brownian motion (random walk) = r = drift + standard_deviation* e^r
mean = logReturns.mean()
variance = logReturns.var()
### Calculate drift which estimates how far the stock price will move in the future
drift = mean - (0.5 * variance)
standard_deviation = logReturns.std()
### Next needed component of brownina motion is a randomly generated variable, such as Z (Z-score), we are projecting how far the stock will deviate from the mean
simulations = 20
probability_z = norm.ppf(np.random.rand(simulations,2))
time_interval = 500 #Number of days into the future we go
dailyReturns = np.exp(drift + standard_deviation * norm.ppf(np.random.rand(time_interval, simulations))) # Estimate of returns
# Starting point of our analyysis is S_0, which is the last historical trading today (today)
S_0 = stock_close.iloc[-1]
# Create an array with estimated stock movements
prices = np.zeros_like(dailyReturns) # Empty array of 0s
prices[0] = S_0
for t in range(1, time_interval):
prices[t] = prices[t-1] * dailyReturns[t]
figMC, axMC = plt.subplots(figsize = (18,12))
axMC.set_xlabel('Days into the Future')
axMC.set_ylabel('Estimated Price')
axMC.set_title('%s - Monte Carlo Stock Forecasting'%i)
axMC.plot(prices)
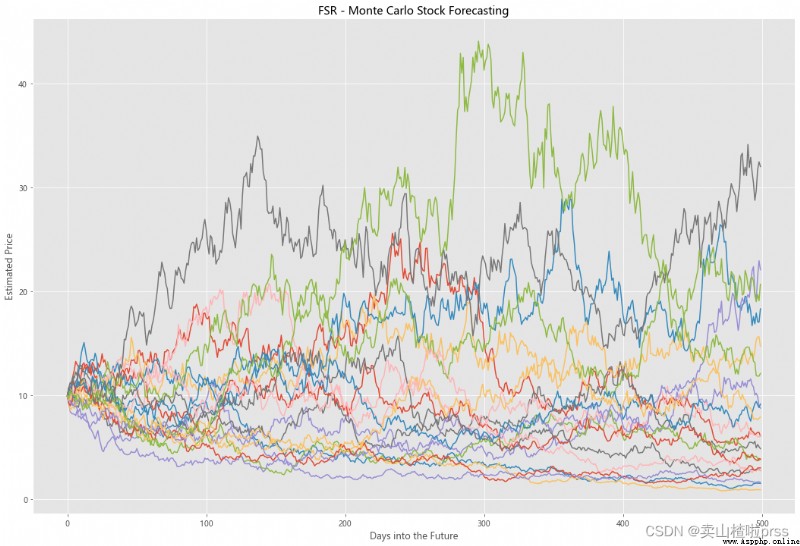
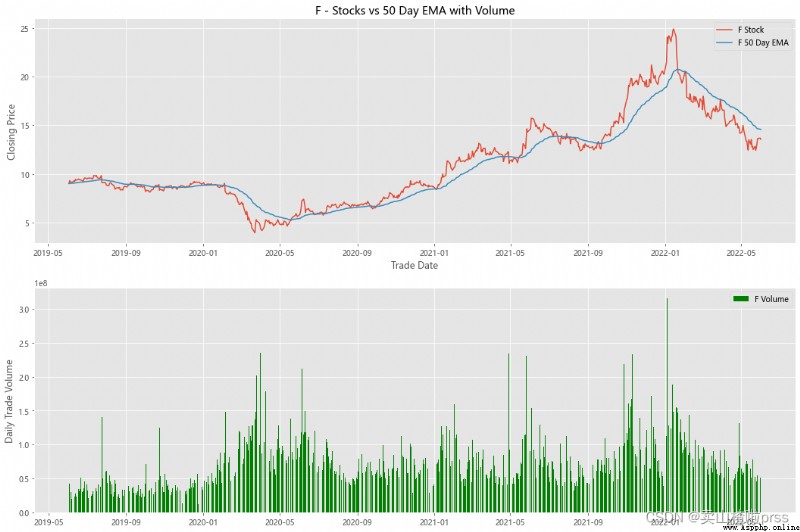
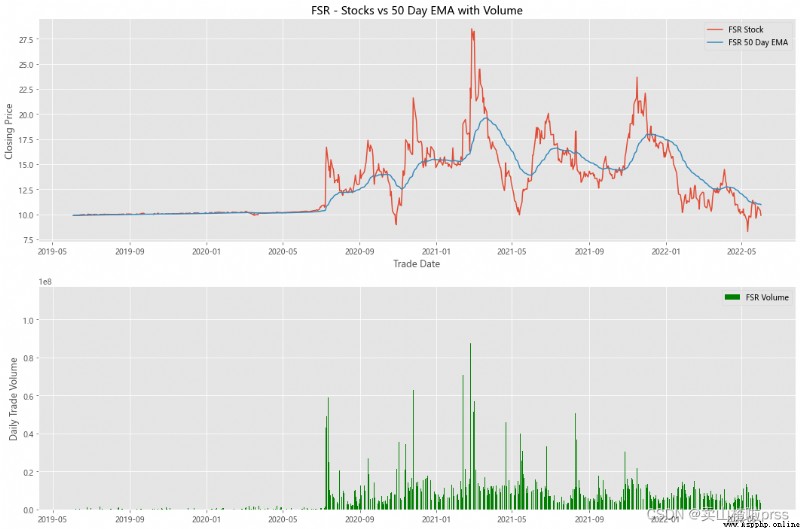
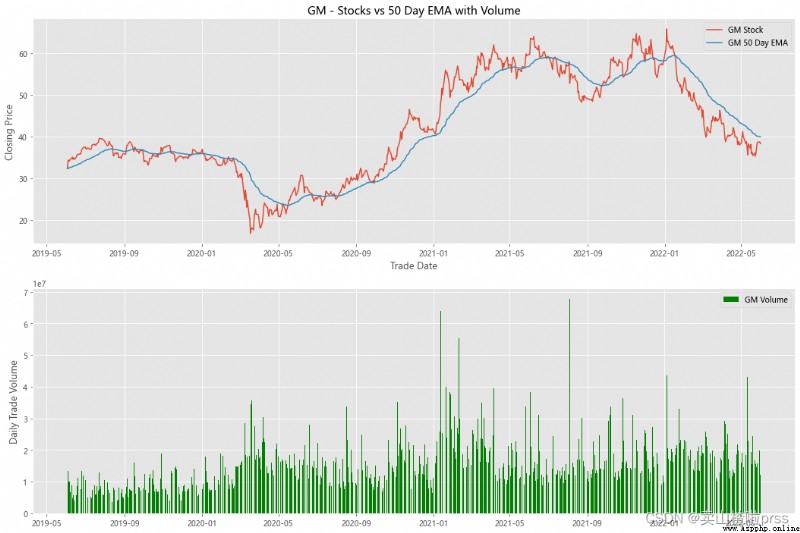
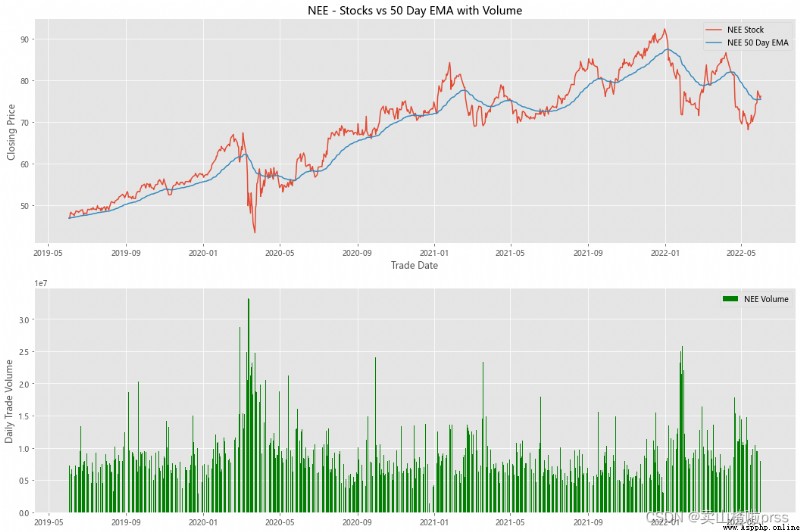
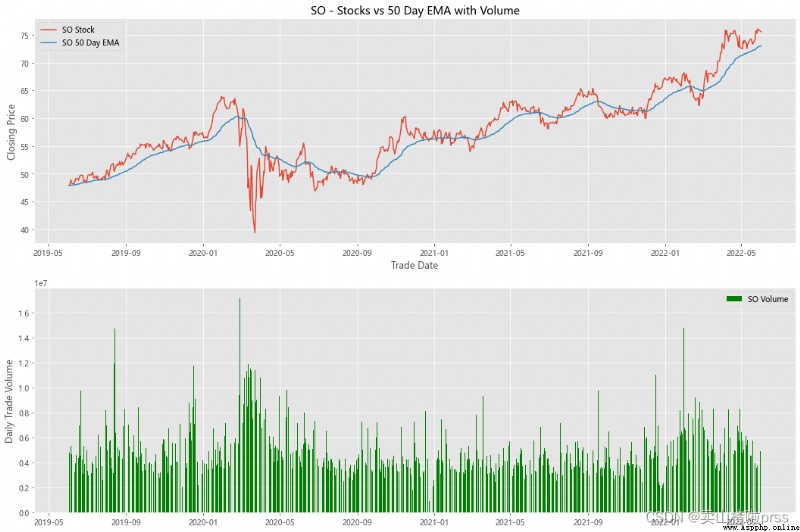
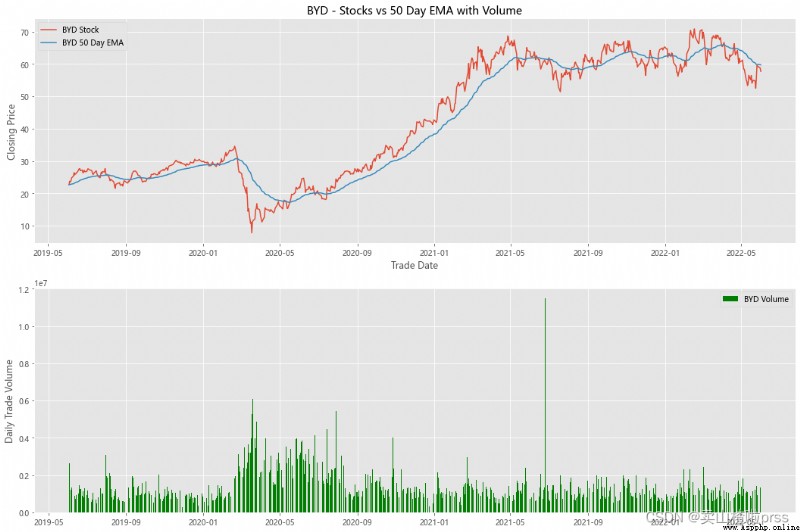
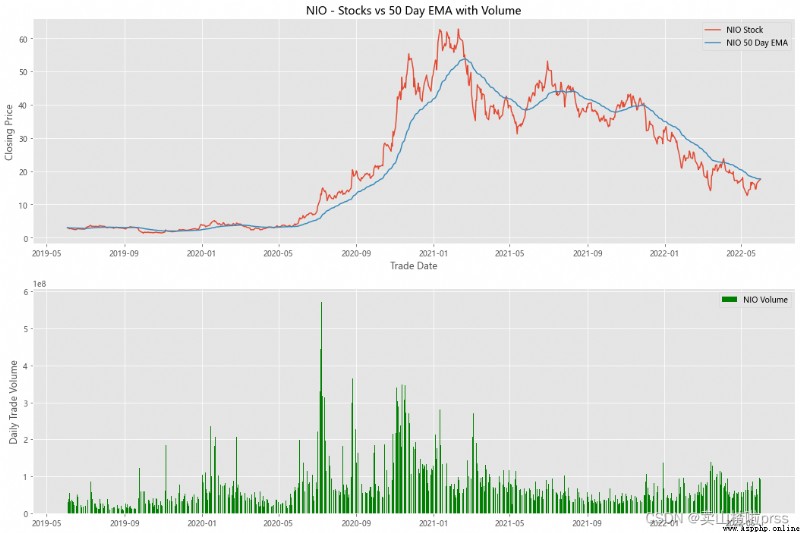
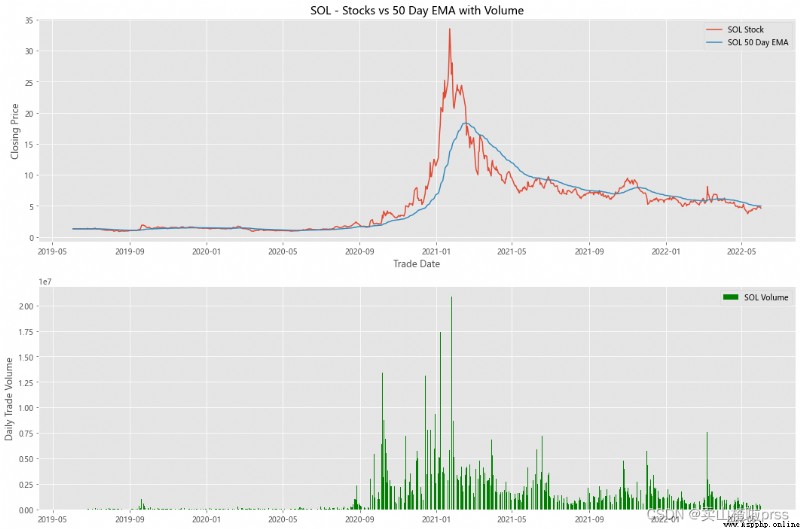
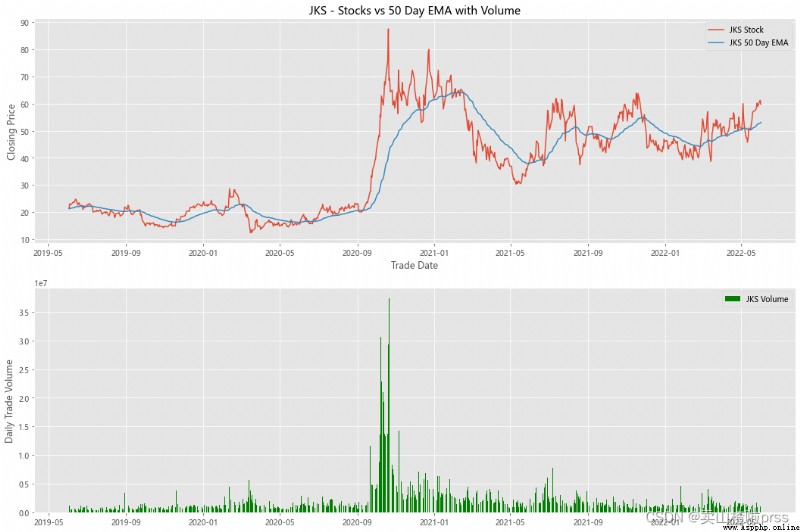
alculate Exponential Moving Averages and Volume
# 計算股票的指數移動平均值和交易量
for i in tickers:
stock_close = stocks[i]
fig3, (ax3,ax4) = plt.subplots(2,1,figsize = (18,12))
emaShort = stock_close.ewm(span=50, adjust=False).mean()
ax3.plot(stock_close.index, stock_close, label = '{} Stock'.format(i))
ax3.plot(emaShort.index, emaShort, label = '{} 50 Day EMA'.format(i))
ax3.set_xlabel('Trade Date')
ax3.set_ylabel('Closing Price')
ax3.set_title('%s - Stocks vs 50 Day EMA with Volume'%i)
ax3.legend()
volume = eval(i)['Volume']
ax4.bar(volume.index, volume, label = '{} Volume'.format(i), color='green')
ax4.set_ylabel('Daily Trade Volume')
ax4.legend()

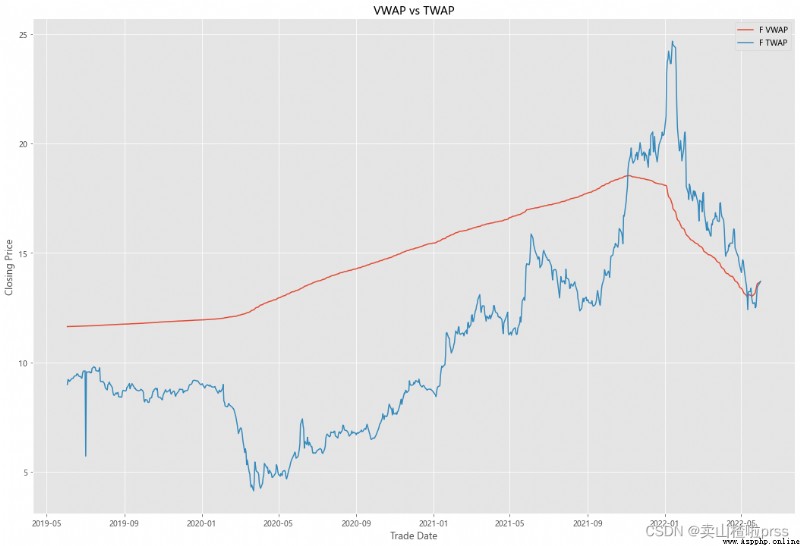
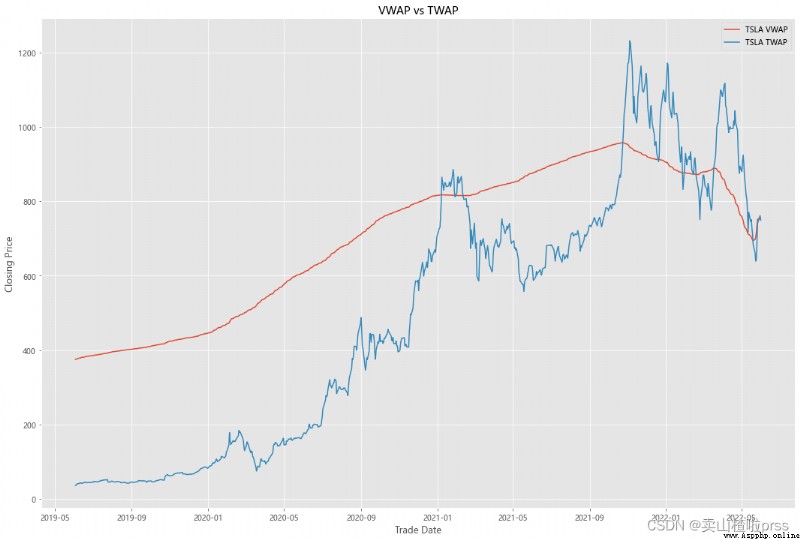
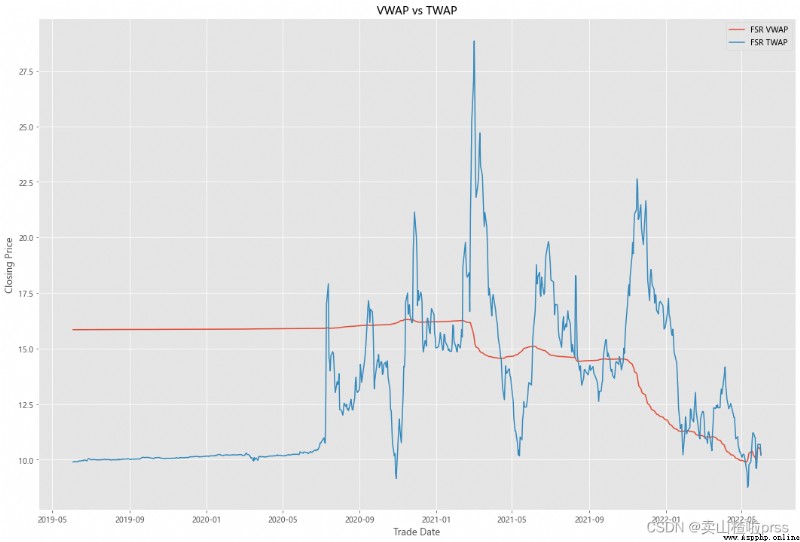
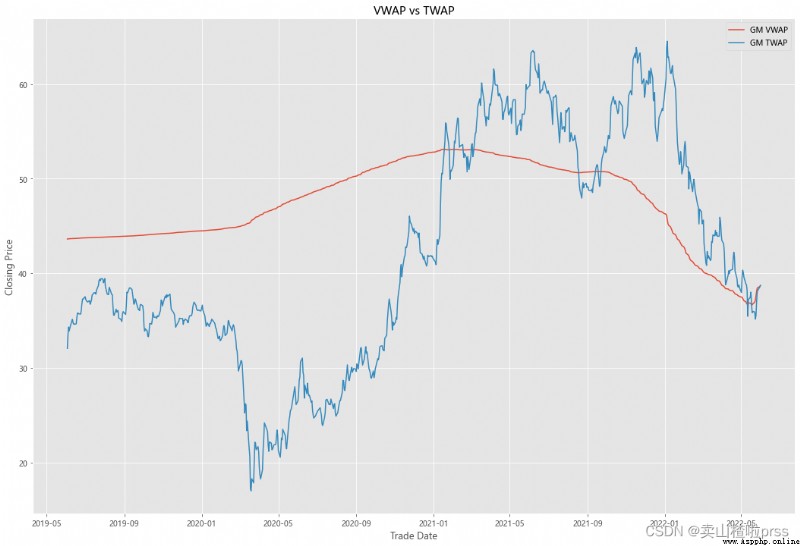
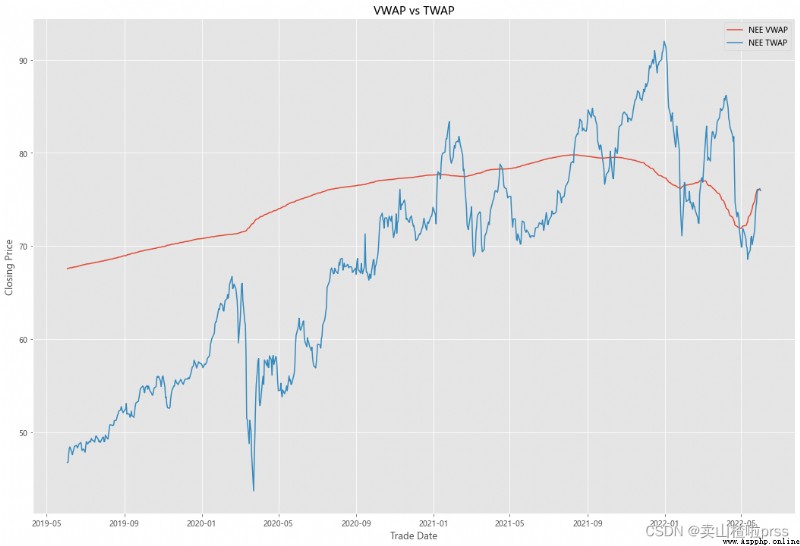
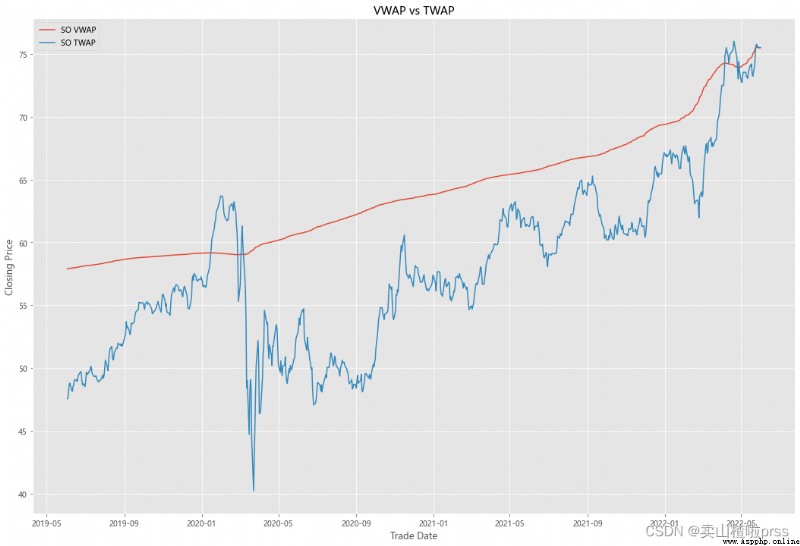
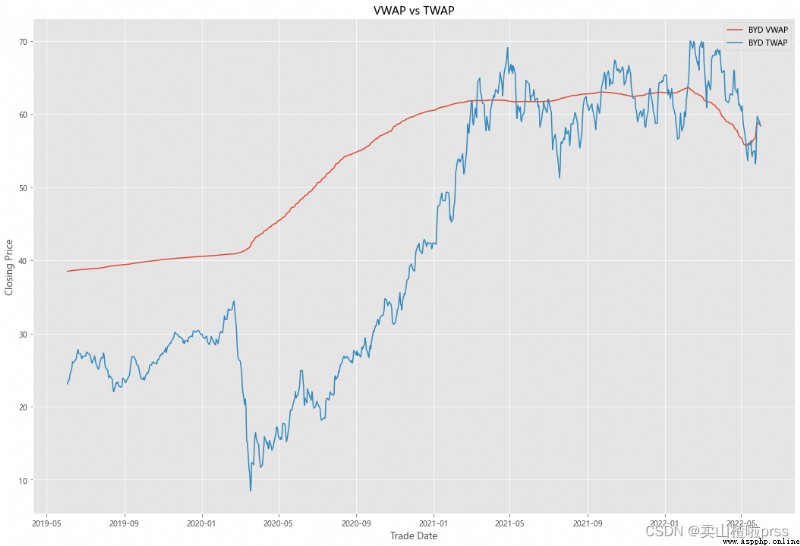
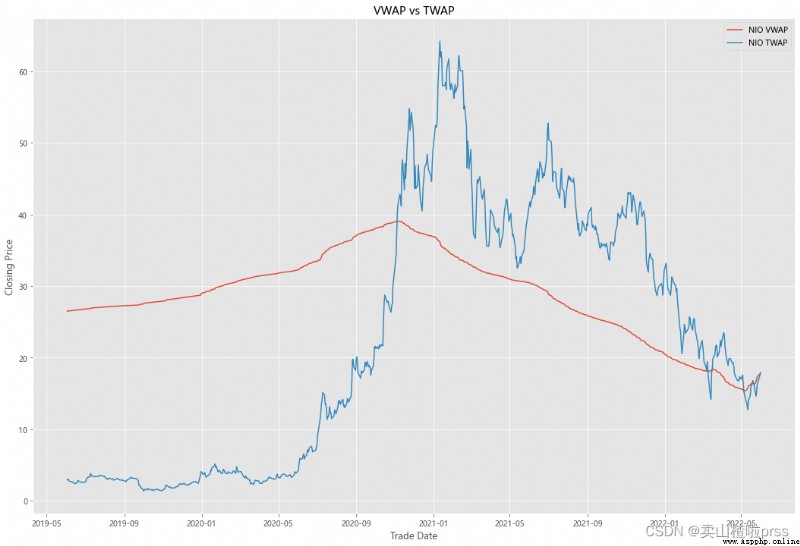
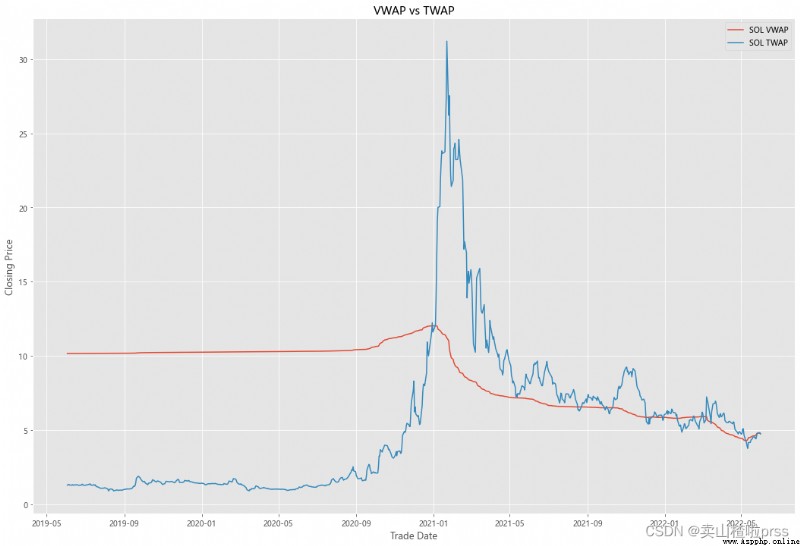
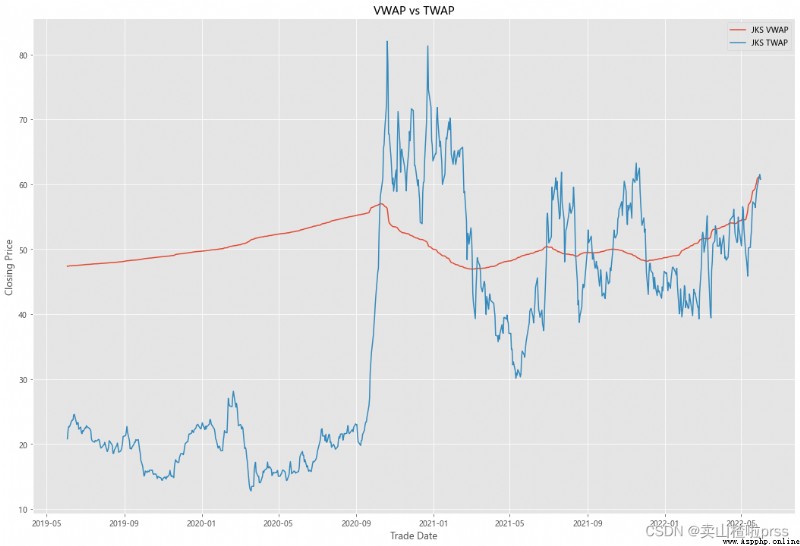
VWAP
#### Quick VWAP Calculation - This is better done with daily intraday data (1 minute ticks), since we dont have that, we are looking at just daily data
for i in tickers:
VWAP = eval(i)
VWAP['cumVol'] = VWAP['Volume'].cumsum()
VWAP['cumVolPrice'] = (VWAP['Volume'] * ((VWAP['High']+VWAP['Low']+VWAP['Open']+VWAP['Close'])/4)).cumsum()
VWAP['VWAP'] = VWAP['cumVolPrice']/VWAP['cumVol']
#### Quick TWAP Calculation
VWAP['TWAP'] = (VWAP['High']+VWAP['Low']+VWAP['Open']+VWAP['Close'])/4
fig5, ax5 = plt.subplots(figsize = (18,12))
ax5.plot(VWAP.index, VWAP['VWAP'], label = '{} VWAP'.format(i))
ax5.plot(VWAP.index, VWAP['TWAP'], label = '{} TWAP'.format(i))
ax5.set_xlabel('Trade Date')
ax5.set_ylabel('Closing Price')
ax5.set_title('VWAP vs TWAP')
ax5.legend()
至此