人工智能

第六章 支持向量機（分類模型）

一、基本概念

1. 什麼是支持向量機

• “支持向量機”（SVM）是一種有監督的機器學習算法，可用於分類任務或回歸任務。主要使用於分類問題。在這個算法中，我們將每個數據項繪制為n維空間中的一個點（其中n是你擁有的特征的數量），每個特征的值是特定坐標的值。然後，我們通過找到最優分類超平面來執行分類任務。
• 支持向量機（Support Vector Machines）是一種二分類模型，在機器學習、計算機視覺、數據挖掘中廣泛應用，主要用於解決數據分類問題，它的目的是尋找一個超平面來對樣本進行分割，分割的原則是間隔最大化（即數據集的邊緣點到分界線的距離d最大，如下圖），最終轉化為一個凸二次規劃問題來求解。通常SVM用於二元分類問題，對於多元分類可將其分解為多個二元分類問題，再進行分類。所謂“支持向量”，就是下圖中虛線穿過的邊緣點。支持向量機就對應著能將數據正確劃分並且間隔最大的直線（下圖中紅色直線）。
  

2. 最優分類邊界

• 什麼才是最優分類邊界？什麼條件下的分類邊界為最優邊界呢？
  
• 如圖中的A，B兩個樣本點，B點被預測為正類的確信度要大於A點，所以SVM的目標是尋找一個超平面，使得離超平面較近的異類點之間能有更大的間隔，即不必考慮所有樣本點，只需讓求得的超平面使得離它近的點間隔最大。超平面可以用如下線性方程來描述：
  w T x + b = 0 w^T x + b = 0 wTx+b=0
  其中， x = ( x 1 ; x 2 ; . . . ; x n ) x=(x_1;x_2;...;x_n) x=(x1​;x2​;...;xn​)， w = ( w 1 ; w 2 ; . . . ; w n ) w=(w_1;w_2;...;w_n) w=(w1​;w2​;...;wn​)， b b b為偏置項. 可以從數學上證明，支持向量到超平面距離為：
  γ = 1 ∣ ∣ w ∣ ∣ \gamma = \frac{1}{||w||} γ=∣∣w∣∣1​
  為了使距離最大，只需最小化 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣即可.

3. SVM最優邊界要求

• SVM尋找最優邊界時，需滿足以下幾個要求：

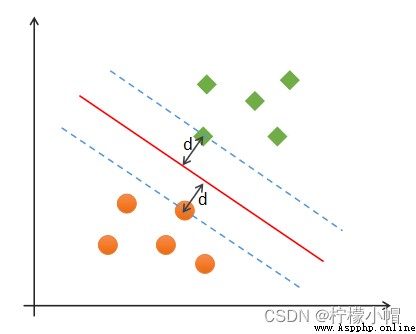
（1）正確性：對大部分樣本都可以正確劃分類別；

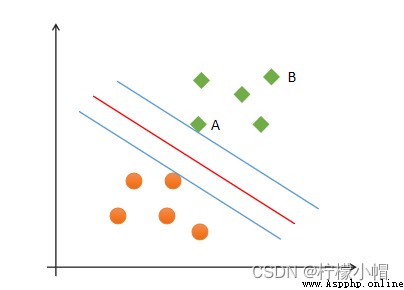
（2）安全性：支持向量，即離分類邊界最近的樣本之間的距離最遠；

（3）公平性：支持向量與分類邊界的距離相等；

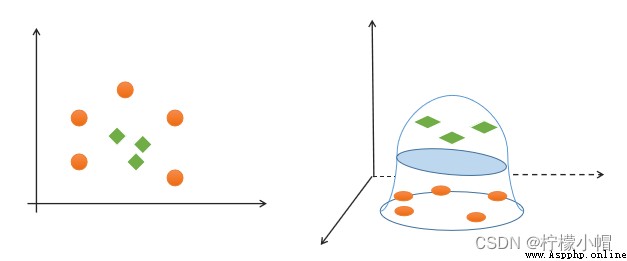
（4）簡單性：采用線性方程（直線、平面）表示分類邊界，也稱分割超平面。如果在原始維度中無法做線性劃分，那麼就通過升維變換，在更高維度空間尋求線性分割超平面. 從低緯度空間到高緯度空間的變換通過核函數進行。

4. 線性可分與線性不可分

① 線性可分

如果一組樣本能使用一個線性函數將樣本正確分類，稱這些數據樣本是線性可分的。那麼什麼是線性函數呢？在二維空間中就是一條直線，在三維空間中就是一個平面，以此類推，如果不考慮空間維數，這樣的線性函數統稱為超平面。

② 線性不可分

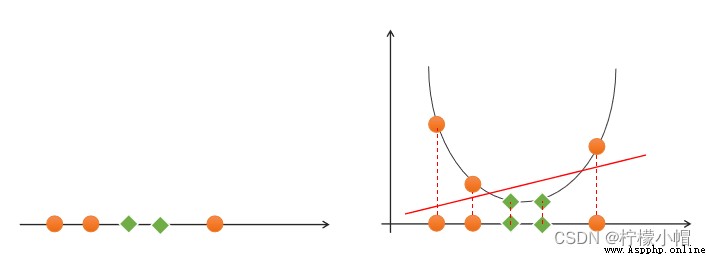
如果一組樣本，無法找到一個線性函數將樣本正確分類，則稱這些樣本線性不可分。以下是一個一維線性不可分的示例：

• 以下是一個二維不可分的示例：
  
• 對於該類線性不可分問題，可以通過升維，將低緯度特征空間映射為高緯度特征空間，實現線性可分，如下圖所示：
  

• 那麼如何實現升維？這就需要用到核函數。

二、支持向量機的原理

• “支持向量機”任務的核心是：尋求最優分類邊界。最優分類邊界應有如下特性：
  • 正確：對大部分樣本可以正確地劃分類別。
  • 泛化：最大化支持向量間距。
  • 公平：與支持向量等距。
  • 簡單：線性，直線或平面，超平面。

三、支持向量機的核函數

• SVM 通過名為核函數的特征變換，可以增加新的特征，使得低維度空間中的線性不可分問題在高維度空間變得線性可分。
• 如果低維空間存在K(x，y)，x，y∈Χ，使得K(x，y)=ϕ(x)·ϕ(y)，則稱K(x，y)為核函數，其中ϕ(x)·ϕ(y)為x，y映射到特征空間上的內積，ϕ(x)為X→H的映射函數。
• 以下是幾種常用的核函數。

1. 線性核函數

• 線性核函數：linear，不通過核函數進行維度提升，僅在原始維度空間中尋求線性分類邊界，主要用於線性可分問題。

# 支持向量機示例
import numpy as np
import sklearn.model_selection as ms
import sklearn.svm as svm
import sklearn.metrics as sm
import matplotlib.pyplot as mp
x, y = [], []
with open("../data/multiple2.txt", "r") as f:
for line in f.readlines():
data = [float(substr) for substr in line.split(",")]
x.append(data[:-1]) # 輸入
y.append(data[-1]) # 輸出
# 列表轉數組
x = np.array(x)
y = np.array(y, dtype=int)
# 線性核函數支持向量機分類器
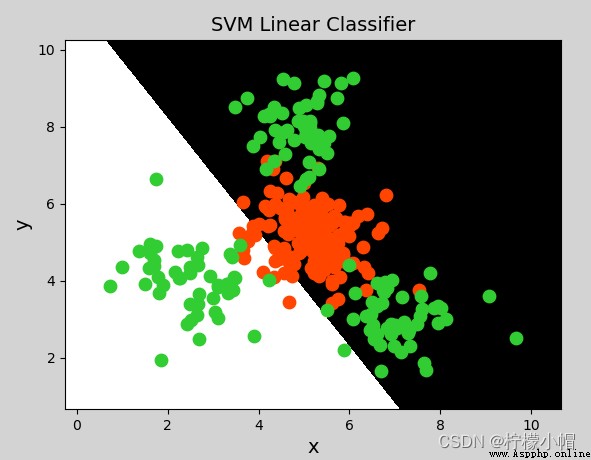
model = svm.SVC(kernel="linear") # 線性核函數
# model = svm.SVC(kernel="poly", degree=3) # 多項式核函數
# print("gamma:", model.gamma)
# 徑向基核函數支持向量機分類器
# model = svm.SVC(kernel="rbf",
# gamma=0.01, # 概率密度標准差
# C=200) # 概率強度
model.fit(x, y)
# 計算圖形邊界
l, r, h = x[:, 0].min() - 1, x[:, 0].max() + 1, 0.005
b, t, v = x[:, 1].min() - 1, x[:, 1].max() + 1, 0.005
# 生成網格矩陣
grid_x = np.meshgrid(np.arange(l, r, h), np.arange(b, t, v))
flat_x = np.c_[grid_x[0].ravel(), grid_x[1].ravel()] # 合並
flat_y = model.predict(flat_x) # 根據網格矩陣預測分類
grid_y = flat_y.reshape(grid_x[0].shape) # 還原形狀
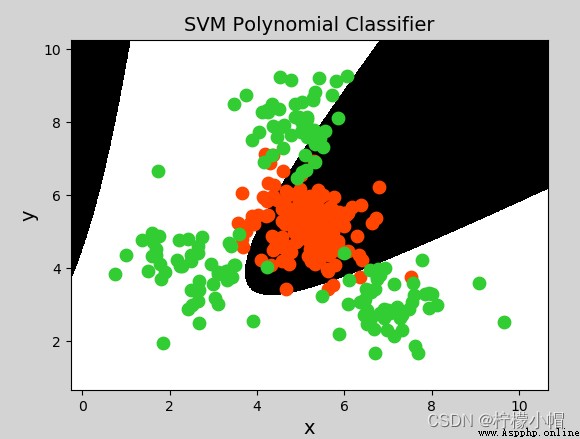
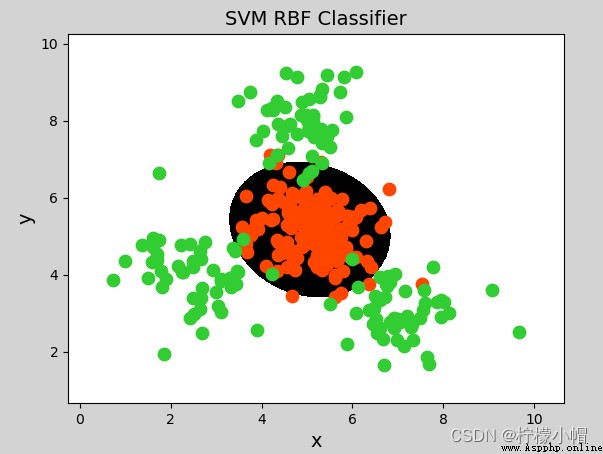
mp.figure("SVM Classifier", facecolor="lightgray")
mp.title("SVM Classifier", fontsize=14)
mp.xlabel("x", fontsize=14)
mp.ylabel("y", fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x[0], grid_x[1], grid_y, cmap="gray")
C0, C1 = (y == 0), (y == 1)
mp.scatter(x[C0][:, 0], x[C0][:, 1], c="orangered", s=80)
mp.scatter(x[C1][:, 0], x[C1][:, 1], c="limegreen", s=80)
mp.show()

2. 多項式核函數

• 多項式核函數：poly，通過多項式函數增加原始樣本特征的高次方冪。
• 多項式核函數（Polynomial Kernel）用增加高次項特征的方法做升維變換，當多項式階數高時復雜度會很高，其表達式為：
  K ( x ， y ) = ( α x T ⋅ y + c ) d K(x，y)=(αx^T·y+c)d K(x，y)=(αxT⋅y+c)d

y = x 1 + x 2 y = x 1 2 + 2 x 1 x 2 + x 2 2 y = x 1 3 + 3 x 1 2 x 2 + 3 x 1 x 2 2 + x 2 3 y = x_1 + x_2\\ y = x_1^2 + 2x_1x_2+x_2^2\\ y=x_1^3 + 3x_1^2x_2 + 3x_1x_2^2 + x_2^3 y=x1​+x2​y=x12​+2x1​x2​+x22​y=x13​+3x12​x2​+3x1​x22​+x23​

• 其中，α表示調節參數，d表示最高次項次數，c為可選常數。
• 示例代碼（將上一示例中創建支持向量機模型改為一下代碼即可）：

model = svm.SVC(kernel="poly", degree=3) # 多項式核函數

3. 徑向基核函數

• 徑向基核函數：rbf，通過高斯分布函數增加原始樣本特征的分布概率。
• 徑向基核函數（Radial Basis Function Kernel）具有很強的靈活性，應用很廣泛。與多項式核函數相比，它的參數少，因此大多數情況下，都有比較好的性能。在不確定用哪種核函數時，可優先驗證高斯核函數。由於類似於高斯函數，所以也稱其為高斯核函數。
• 示例代碼（將上一示例中分類器模型改為如下代碼即可）：

# 徑向基核函數支持向量機分類器
model = svm.SVC(kernel="rbf",
gamma=0.01, # 概率密度標准差
C=600) # 概率強度，該值越大對錯誤分類的容忍度越小，分類精度越高，但泛化能力越差；該值越小，對錯誤分類容忍度越大，但泛化能力強

4. 總結

• SVM 線性核函數的 sklearn 實現如下：

model = svm.SVC(kernel='linear')
model.fit(train_x, train_y)

• SVM 多項式核函數的 sklearn 實現如下：

# 基於線性核函數的支持向量機分類器
model = svm.SVC(kernel='poly', degree=3)
model.fit(train_x, train_y)

• SVM 徑向基核函數的 sklearn 實現如下：

# 基於徑向基核函數的支持向量機分類器
# C：正則強度
# gamma：'rbf','poly'和'sigmoid'的內核函數。伽馬值越高，則會精確擬合訓練數據集，有可能導致過擬合問題。
model = svm.SVC(kernel='rbf', C=600, gamma=0.01)
model.fit(train_x, train_y)

（1）支持向量機是二分類模型

（2）支持向量機通過尋找最優線性模型作為分類邊界

（3）邊界要求：正確性、公平性、安全性、簡單性

（4）可以通過核函數將線性不可分轉換為線性可分問題，核函數包括：線性核函數、多項式核函數、徑向基核函數

（5）支持向量機適合少量樣本的分類

四、網格搜索

• 獲取一個最優超參數的方式可以繪制驗證曲線，但是驗證曲線只能每次獲取一個最優超參數。如果多個超參數有很多排列組合的話，就可以使用網格搜索尋求最優超參數組合。
• 針對超參數組合列表中的每一個超參數組合，實例化給定的模型，做cv次交叉驗證，將其中平均f1得分最高的超參數組合作為最佳選擇，實例化模型對象並返回。
• 網格搜索相關API：

import sklearn.model_selection as ms
params =
[{
'kernel':['linear'], 'C':[1, 10, 100, 1000]},
{
'kernel':['poly'], 'C':[1], 'degree':[2, 3]},
{
'kernel':['rbf'], 'C':[1,10,100], 'gamma':[1, 0.1, 0.01]}]
model = ms.GridSearchCV(模型, params, cv=交叉驗證次數)
model.fit(輸入集，輸出集)
# 獲取網格搜索每個參數組合
model.cv_results_['params']
# 獲取網格搜索每個參數組合所對應的平均測試分值
model.cv_results_['mean_test_score']
# 獲取最好的參數
model.best_params_
model.best_score_
model.best_estimator_

五、案例：支持向量機實現

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
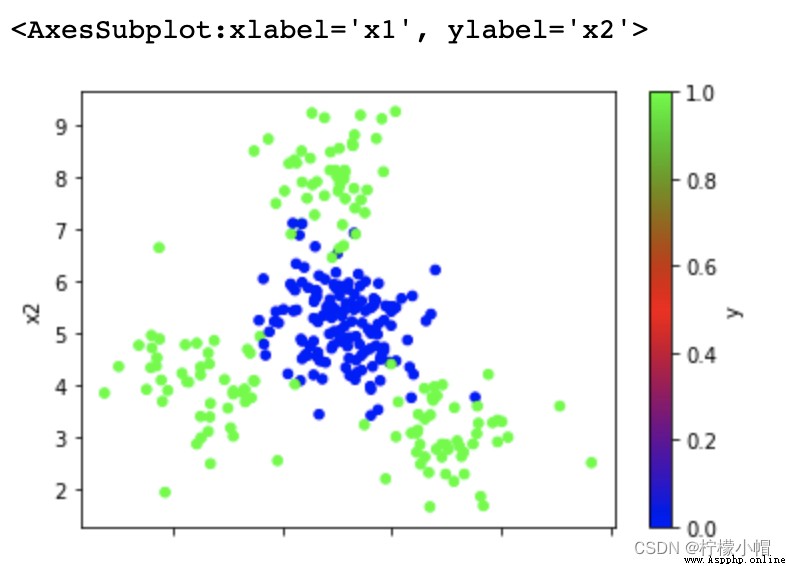
data = pd.read_csv('multiple2.txt', header=None, names=['x1', 'x2', 'y'])
data.plot.scatter(x='x1', y='x2', c='y', cmap='brg')

import sklearn.model_selection as ms
import sklearn.svm as svm
import sklearn.metrics as sm
# 整理數據集，拆分測試集訓練集
x, y = data.iloc[:, :-1], data['y']
train_x, test_x, train_y, test_y = ms.train_test_split(x, y, test_size=0.25, random_state=7)
model = svm.SVC(kernel='linear')
model.fit(train_x, train_y)
pred_test_y = model.predict(test_x)
print(sm.classification_report(test_y, pred_test_y))
""" precision recall f1-score support 0 0.69 0.90 0.78 40 1 0.83 0.54 0.66 35 accuracy 0.73 75 macro avg 0.76 0.72 0.72 75 weighted avg 0.75 0.73 0.72 75 """
data.head()
""" x1 x2 y 0 5.35 4.48 0 1 6.72 5.37 0 2 3.57 5.25 0 3 4.77 7.65 1 4 2.25 4.07 1 """

# 暴力繪制分類邊界線
# 從x的min-max，拆出100個x坐標
# 從y的min-max，拆出100個y坐標
# 一共組成10000個坐標點，預測每個坐標點的類別標簽，繪制散點
xs = np.linspace(data['x1'].min(), data['x1'].max(), 100)
ys = np.linspace(data['x2'].min(), data['x2'].max(), 100)
points = []
for x in xs:
for y in ys:
points.append([x, y])
points = np.array(points)
# 預測每個坐標點的類別標簽 繪制散點
point_labels = model.predict(points)
plt.scatter(points[:,0], points[:,1], c=point_labels, cmap='gray')
plt.scatter(test_x['x1'], test_x['x2'], c=test_y, cmap='brg')

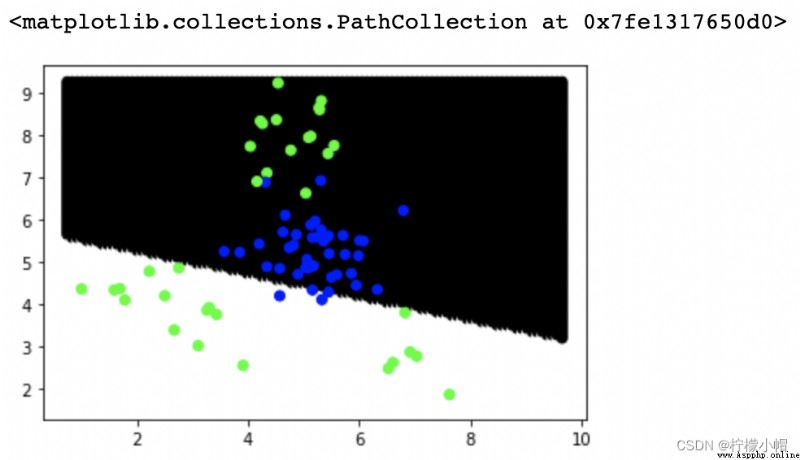
# 多項式核函數
model = svm.SVC(kernel='poly', degree=2)
model.fit(train_x, train_y)
pred_test_y = model.predict(test_x)
print(sm.classification_report(test_y, pred_test_y))
# 預測每個坐標點的類別標簽 繪制散點
point_labels = model.predict(points)
plt.scatter(points[:,0], points[:,1], c=point_labels, cmap='gray')
plt.scatter(test_x['x1'], test_x['x2'], c=test_y, cmap='brg')
""" precision recall f1-score support 0 0.84 0.95 0.89 40 1 0.93 0.80 0.86 35 accuracy 0.88 75 macro avg 0.89 0.88 0.88 75 weighted avg 0.89 0.88 0.88 75 """

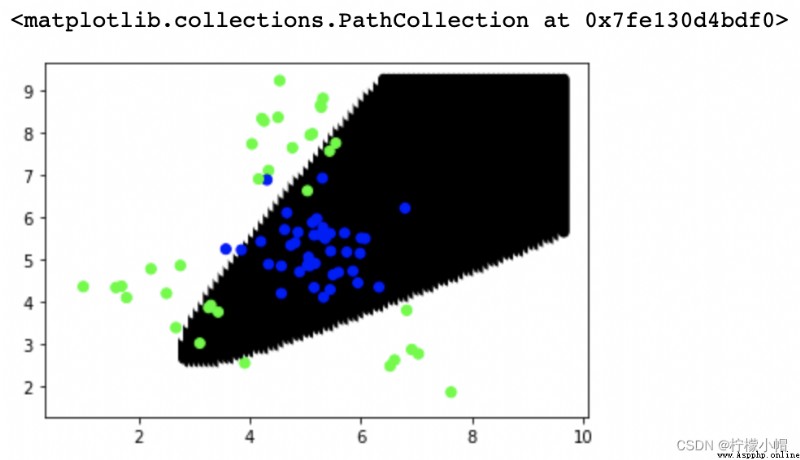
# 徑向基核函數
model = svm.SVC(kernel='rbf', C=1, gamma=0.1)
model.fit(train_x, train_y)
pred_test_y = model.predict(test_x)
# print(sm.classification_report(test_y, pred_test_y))
# 預測每個坐標點的類別標簽 繪制散點
point_labels = model.predict(points)
plt.scatter(points[:,0], points[:,1], c=point_labels, cmap='gray')
plt.scatter(test_x['x1'], test_x['x2'], c=test_y, cmap='brg')
""" precision recall f1-score support 0 0.97 0.97 0.97 40 1 0.97 0.97 0.97 35 accuracy 0.97 75 macro avg 0.97 0.97 0.97 75 weighted avg 0.97 0.97 0.97 75 """

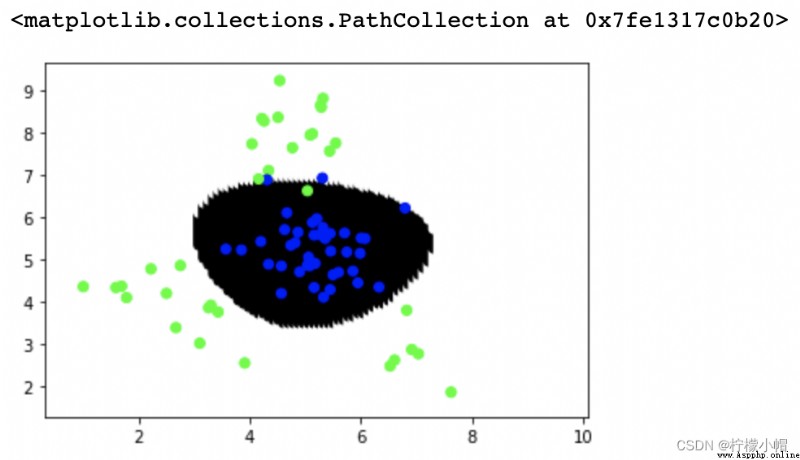
# 通過網格搜索尋求最優超參數組合
model = svm.SVC()
# 網格搜索
params = [{
'kernel':['linear'], 'C':[1, 10, 100]},
{
'kernel':['poly'], 'degree':[2, 3]},
{
'kernel':['rbf'], 'C':[1, 10, 100], 'gamma':[1, 0.1, 0.001]}]
model = ms.GridSearchCV(model, params, cv=5)
model.fit(train_x, train_y)
pred_test_y = model.predict(test_x)
# print(sm.classification_report(test_y, pred_test_y))
# 預測每個坐標點的類別標簽 繪制散點
point_labels = model.predict(points)
plt.scatter(points[:,0], points[:,1], c=point_labels, cmap='gray')
plt.scatter(test_x['x1'], test_x['x2'], c=test_y, cmap='brg')

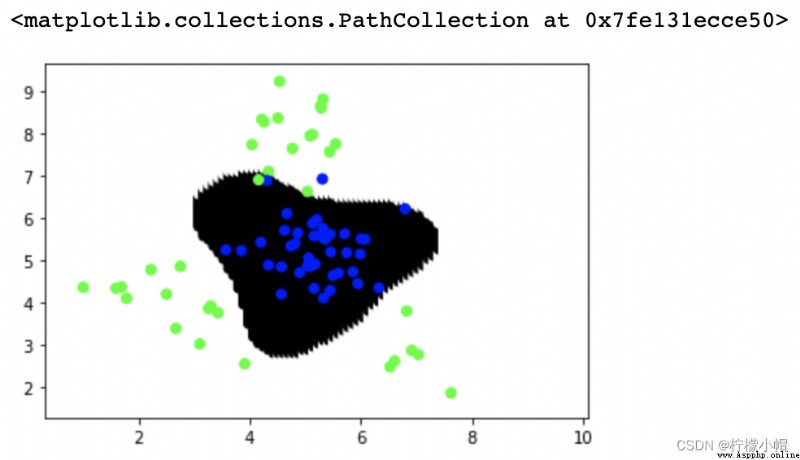
print(model.best_params_)
print(model.best_score_)
print(model.best_estimator_)
""" {'C': 1, 'gamma': 1, 'kernel': 'rbf'} 0.9511111111111111 SVC(C=1, gamma=1) """