1 subject

Here's a button Non decreasing order Sorted array of integers nums, return The square of each number A new array of , According to the requirements Non decreasing order Sort .

2 analysis

（1） Method 1 ： Use python Built in sort The fast line of
Spatial complexity O(n), Time complexity O(nlogn)
（2） Method 2
Direct insert sort , But the time limit is exceeded
Time complexity O ( n 2 ) O(n^2) O(n2), Time complexity O(1)
（3） Method 3
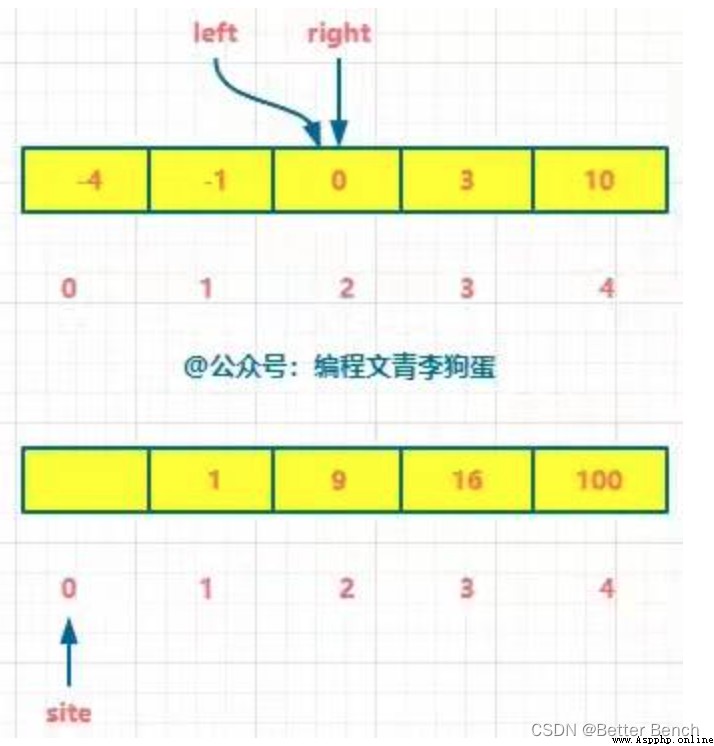
Double pointer
Time complexity O(n), Spatial complexity O(n)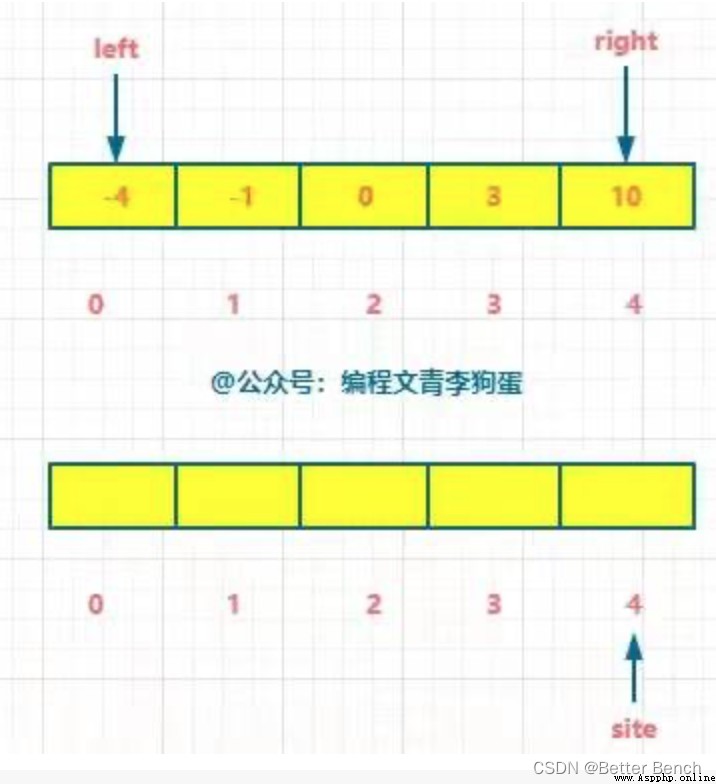

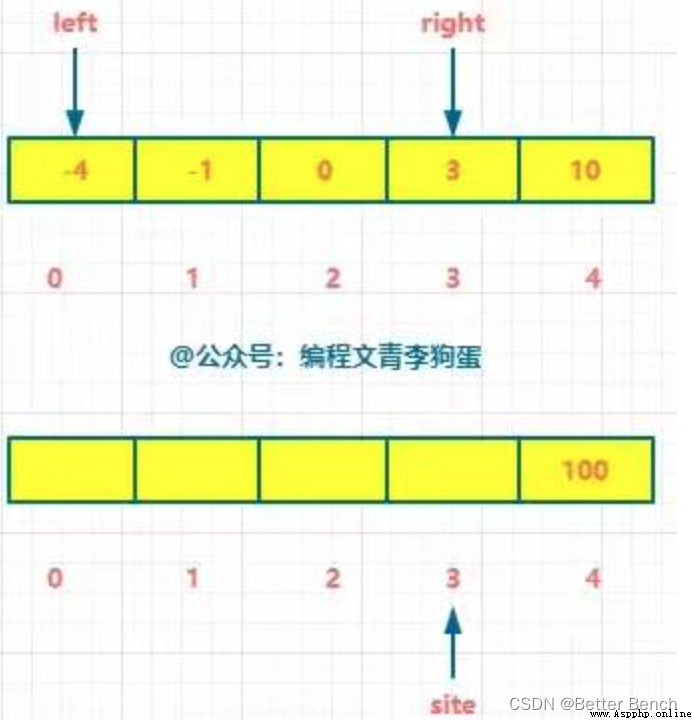
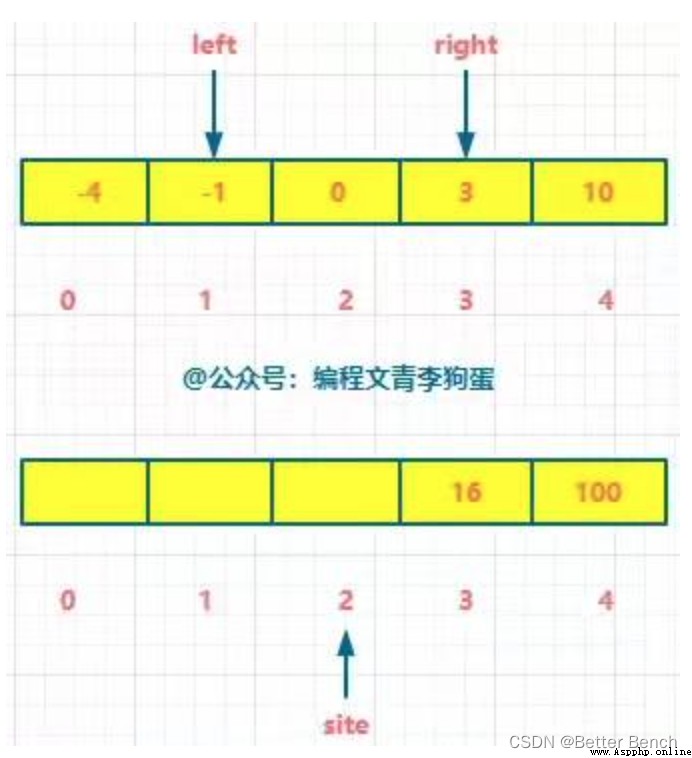
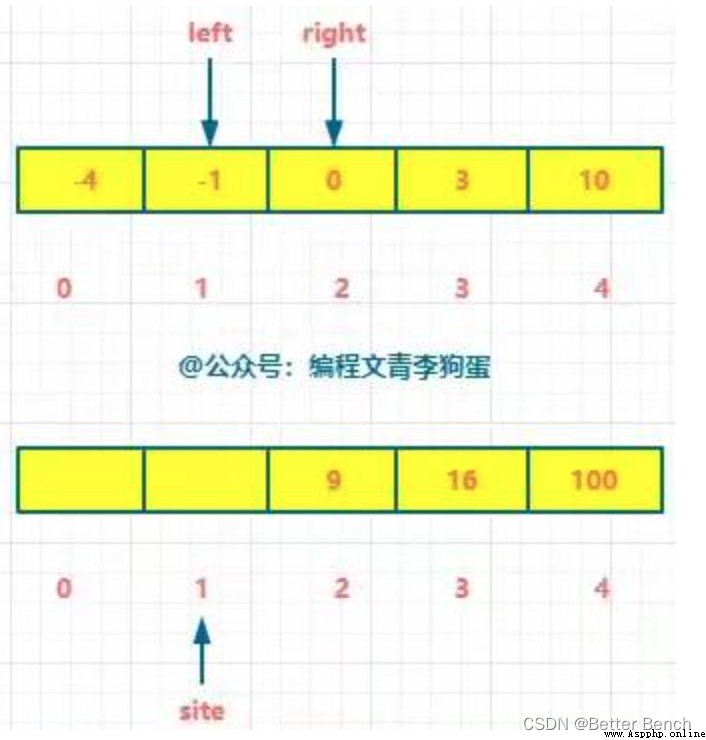
3 python Realization

（1） Method 1

# Quick sort 
def sortedSquares(self, nums: List[int]) -> List[int]:
res = []
for i in nums:
res.append(i*i)
# The first method , Use python Built in sort Method 
res.sort()
# The second method , Write your own fast algorithm 
self.QuckSort(res,0,len(nums)-1)
return res
def partition(self,arr,low,high):
i = low-1
pivot =arr[high]
for j in range(low,high):
if arr[j]<=pivot:
i+=1
arr[i],arr[j] = arr[j],arr[i]
arr[i+1],arr[high] = arr[high],arr[i+1]
return i+1
def QuckSort(self,arr,low,high):
if low <high:
p = self.partition(arr,low,high)
self.QuckSort(arr,low,p-1)
self.QuckSort(arr,p+1,high)

（2） Method 2

 # Direct insert sort ; Be careful , Beyond the time limit 
def sortedSquares(self, nums: List[int]) -> List[int]:
if len(nums)==0:
return nums
nums[0] = nums[0]*nums[0]
for i in range(1,len(nums)):
temp = nums[i]*nums[i]
j=i-1
while j>=0 and temp<nums[j]:
nums[j+1] =nums[j]
j -=1
nums[j+1] = temp
return nums

（3） Method 3

# Double pointer 
def sortedSquares(self, nums: List[int]) -> List[int]:
if len(nums)==1:
return [nums[0]*nums[0]]
res = [-1]*len(nums)
idx = len(nums)-1
right =len(nums)-1
left = 0
while left<=right:
if nums[left]*nums[left]>nums[right]*nums[right]:
res[idx] = nums[left]*nums[left]
left +=1
else:
res[idx] = nums[right]*nums[right]
right -=1
idx -=1
return res