目錄
一、K-Means原理
1.聚類簡介
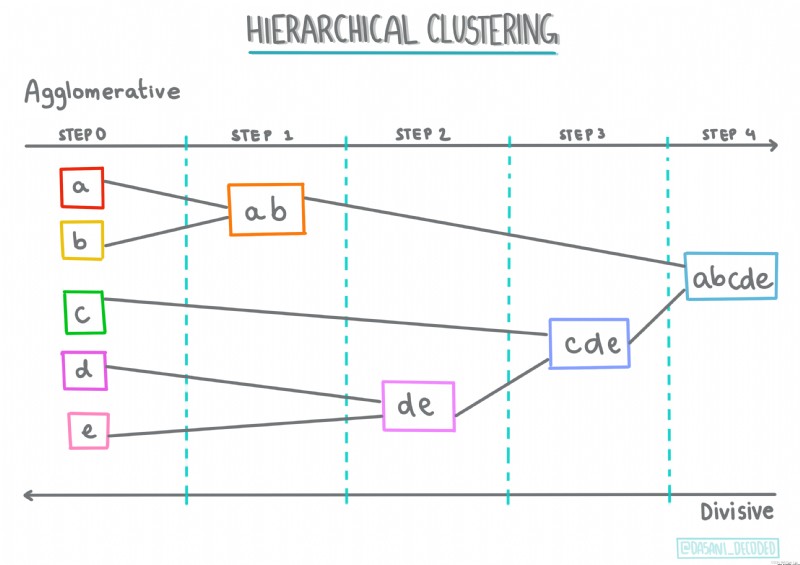
①分層聚類
②質心聚類
③其他聚類
2.K-means的原理
3.K-means的應用場景
二、K-Means的案例實戰
1.數據查看
①數據導入及結構查看
②查看數據描述
2.數據可視化及預處理
①條形圖
②熱力圖
③核密度圖
④散點圖
⑤箱型圖
3.模型訓練與精度評價
①樣本選擇
②模型訓練
③精度評價
④模型調參
三、結論
在本文中，你將學會：
0 K-means的數學原理
1 K-means的Scikit-Learn函數解釋
2 K-means的案例實戰
機器學習算法中有 100 多種聚類算法，它們的使用取決於手頭數據的性質。我們討論一些主要的算法。
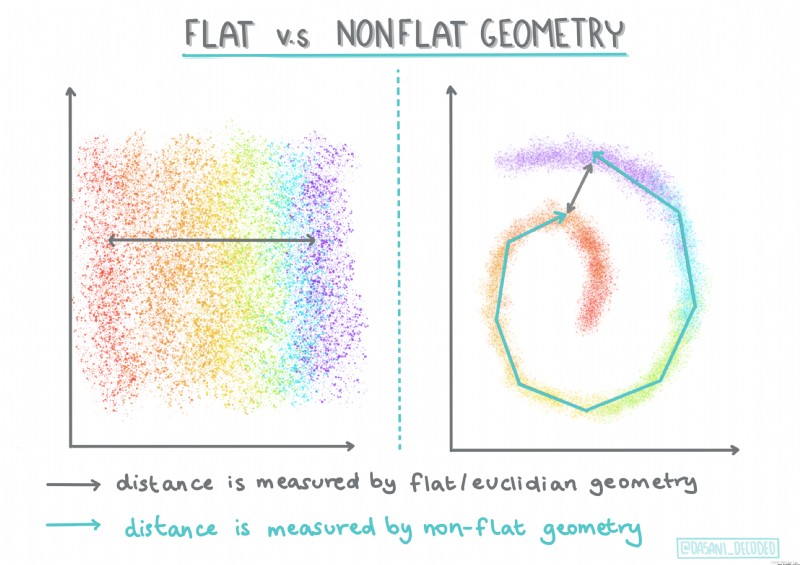
分層聚類。如果一個物體是按其與附近物體的接近程度而不是與較遠物體的接近程度進行分類的，則根據其成員與其他物體之間的距離形成聚類。
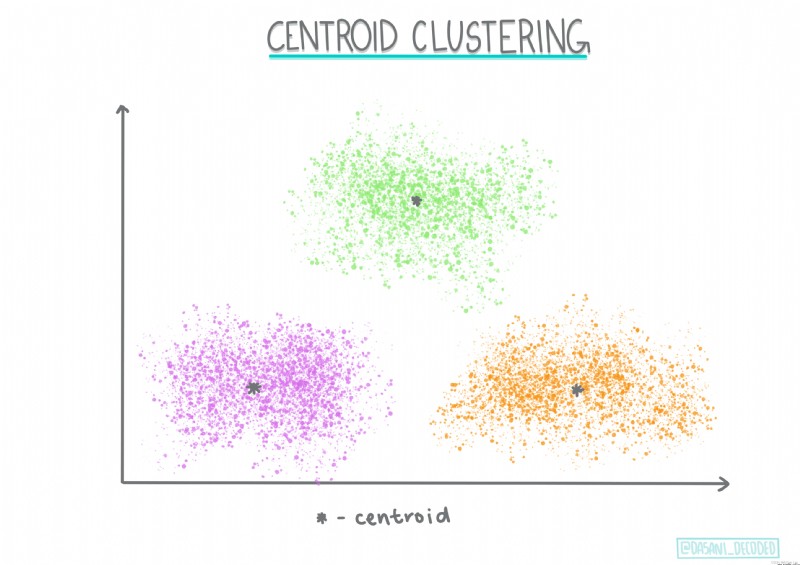
質心聚類。這種流行的聚類算法需要選擇K（聚類數），之後算法確定聚類的質心點並圍繞該點收集數據。K 均值聚類是質心聚類的流行版本。質心由其類別所有樣本點之間的均值確定，因此得名。
基於分布的聚類。基於統計建模，基於分布的聚類分析側重於確定數據點屬於聚類的概率，並相應地分配它。高斯混合方法屬於這種類型。
基於密度的聚類。數據點根據其密度或彼此之間的分組分配給聚類。遠離組的數據點被視為異常值或噪聲。DBSCAN、均值偏移等都屬於這種類型的聚類。
基於網格的群集。對於多維數據集，將創建一個網格，並在網格的單元之間劃分數據，從而創建聚類。
方便學習起見，本文中我們只討論K-Means算法，其他聚類算法我會另外撰文講解。
先講一個經典的K-means故事：
0 從前，有四個牧師去郊區步道，一開始牧師隨便選了幾個布道點，並且把這幾個布道點的情況公告給了郊區所有的居民，於是每個居民到離自己家最近的布道點去聽課。
1 聽課以後，大家覺得距離太遠了，於是每個牧師統計了以下自己的課上所有的居民的地址，搬到了所有地址的中心地帶，並且在海報上更新了自己的布道點的比特置。
2 牧師每一次移動不可能離所有人都更近，有的人發現A牧師移動後自己還不如去B牧師處聽課更近，於是每個居民又去了離自己最近的布道點...就這樣，牧師每個禮拜更新自己的比特置，居民根據自己的情況選擇布道點，最終穩定了下來。
這是K-means的計算步驟：
0 先定義總共有多少個類別（簇）
1 將每個簇心（質心）隨機分配坐標比特置
2 將每個樣本數據點關聯到離該樣本點距離最近的質心上，即分配其類別
3 對於每個簇找到所有關聯點的中心點（樣本與質心歐氏距離的均值）
4 將該均值點作為該類別新的質心
5 如此訓練，直到每個簇所擁有的點比特置不在改變
注意！此過程中，只有質心的比特置在改變，樣本點比特置不變！
這是質心到樣本點的歐式距離計算公式：
這個經典的故事對K均值的理解很有幫助，在故事中，牧師的比特置就是質心，居民家的比特置就是樣本點。牧師比特置的每一次調整就是 一次迭代。不同類型的K-means算法對應的距離計算方法也不同。
0 分檔分類器
1 物品傳輸優化
2 識別事件發生地點
3 用戶分類
4 人員狀態分析
5 保險欺詐檢測
6 乘車數據分析
7 網絡分析犯罪分子
8 泰森多邊形
...
輸入以下代碼，將我們需要的尼日利亞音樂數據集導入notebook並查看其組織結構。
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv("nigerian-songs.csv")#以pandas庫的read_csv函數讀取csv文件
df.head()#查看前5行數據輸出結果如下：
其中有音樂的基本信息（名稱、藝術家、發布日期等），輸入以下代碼，查看其數據結構：
df.info()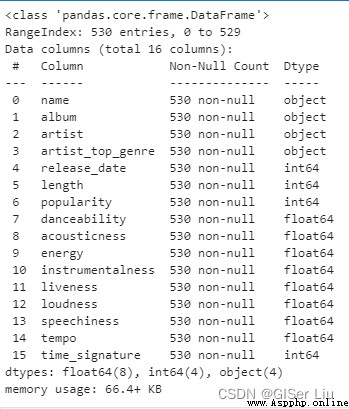
可以看到，尼日利亞音樂數據集中共包含539行樣本。有16個待選擇數據特征：數值型數據有12個，字符型數據有4個。
輸入以下代碼查看數據描述：
df.describe()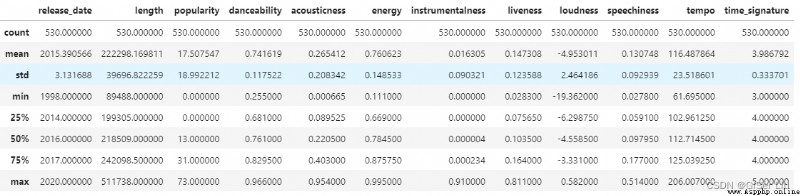
通過查看數據的描述，我們可以看到不同數據特征的數量、均值、方差及不同層次的數值。這些信息可以幫助我們在後面的處理中選擇合適的模型或處理方法。
如果我們使用的是聚類分析，這是一種不需要標記數據的無監督方法，為什麼我們需要這些信息？在數據探索階段，它們會派上用場！
可視化數據，直觀查看數據的特征。本次作者使用seaborn庫來可視化，seaborn庫是基於matplotlib庫封裝的，可視化效果更棒！
在此之前我們去掉數據中包含缺失值的樣本，避免其影響。查看數據是否有缺失值或異常值，輸入以下代碼：
df.isnull().sum()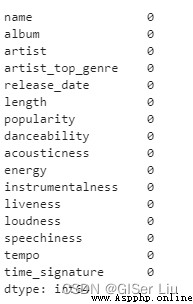
可以看到，本次數據比較幹淨，沒有缺失值。我們開始可視化！
輸入以下代碼查看數據集中數量前5名的藝術家類型數量的條形圖：
import seaborn as sns#導入seaborn包
top = df['artist_top_genre'].value_counts()#對不同音樂家類型進行統計匯總，格式為列錶
plt.figure(figsize=(10,7))#設置圖錶大小
sns.barplot(x=top[:5].index,y=top[:5].values)#取出前5行數據的index作為X軸類型，音樂數量作為Y軸數值繪制條形圖
plt.xticks(rotation=45)#若X軸標簽過長導致可視化效果不好，可進行標簽旋轉進行調整
plt.title('Top genres',color = 'blue')#設置條形圖標題內容及顏色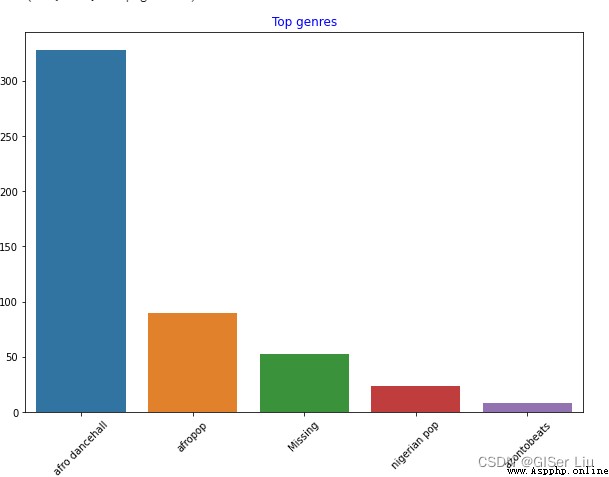
可以看到，前5種風格類型中，afro dancehall風格音樂數量最多；眼尖的同學可能發現，其中有一部分數據是“Missing”，這錶示這部分數據是沒有類型標簽的，方便分析起見，我們將這一部分數據拋棄掉！
在大部分數據集中，🤨類似於"Missing"類型的數據在缺失值篩選中並不容易被發現，但它們常常占據著較大部分，我們可以對這些特征繪制條形圖來發現它們並進行剔除！
繼續對全部數據進行可視化。輸入以下代碼：
df = df[df['artist_top_genre'] != 'Missing']#刪去沒有音樂風格標簽的數據
top = df['artist_top_genre'].value_counts()#統計不同音樂風格的音樂數量
plt.figure(figsize=(10,7))#設置畫布尺寸
sns.barplot(x=top.index,y=top.values)#對所有音樂風格數據的標簽和數量繪制條形圖
plt.xticks(rotation=45)#調整X軸標簽角度
plt.title('Top genres',color = 'blue')#設置標題屬性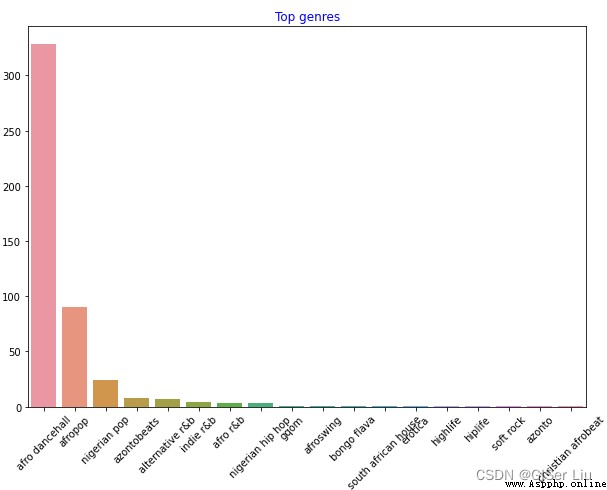
如此一來，不同風格的音樂數據便清晰的展現出來。
為了方便我們的聚類實驗，我們提取出數量最多的三類樣本及人氣大於0的樣本作為數據集主體用於之後的聚類。輸入以下代碼：
df = df[(df['artist_top_genre'] == 'afro dancehall') | (df['artist_top_genre'] == 'afropop') | (df['artist_top_genre'] == 'nigerian pop')]#提取數量前三的樣本
df = df[(df['popularity'] > 0)]#提取人氣大於0的樣本做一個快速測試，看看數據中哪些特征之間存在高度相關。我們對經過篩選的數據進行相關系數計算，並以熱力圖的方式呈現相關性。輸入以下代碼 ：
corrmat = df.corr()#用於計算相關系數
f, ax = plt.subplots(figsize=(12, 9))#subplots() 函數既創建了一個包含子圖區域的畫布，又創建了一個 figure 圖形對象。
sns.heatmap(corrmat, vmax=.8, square=True)#corrmat值為相關系數，vmax為最大相關系數值用來界定顏色的映射範圍，square為bool類型參數，是否使熱力圖的每個單元格為正方形，默認為False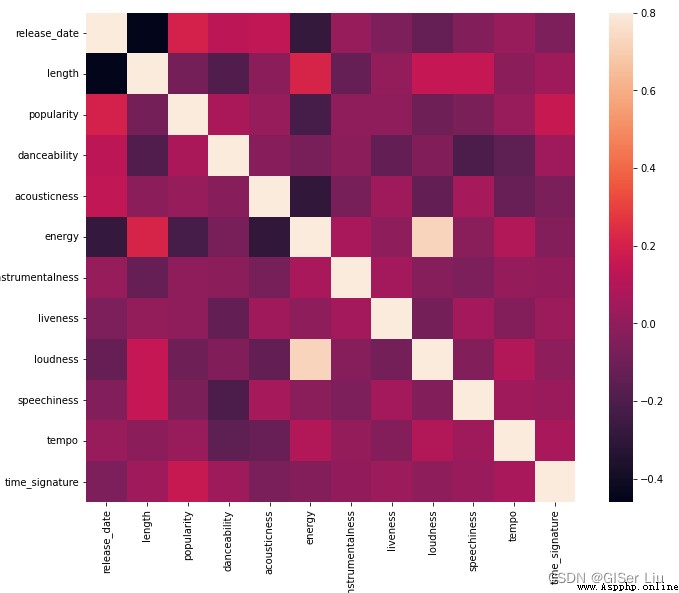
排除矩陣對角線上的相關性（自己與自己本來就高度相關），我們可以看到energy和loudness特征相關形較高。這並不奇怪，因為嘈雜的音樂通常充滿激情。
請注意，相關性並不意味著因果關系！我們證明它們相關，但不能證明他們之間的因果關系。
根據它們的受歡迎程度，這三種流派在可跳舞性的看法上是否顯著不同？以音樂數據的人氣為X軸，以是否可跳舞性為Y軸繪制核密度（KDE）圖查看數據的分布。輸入以下代碼：
sns.set_theme()#set_style( )是用來設置主題的，Seaborn有五個預設好的主題： darkgrid , whitegrid , dark , white ,和 ticks
g = sns.jointplot(#jointplot函數用於繪制雙變量圖
data=df,#數據為經過篩選預處理的數據
x="popularity", y="danceability", hue="artist_top_genre",#選擇兩個變量， 增加hue變量將為圖形添加條件顏色，並在邊沿軸上繪制單獨的密度曲線
kind="kde",#設置繪圖類型 KDE指核密度圖
)
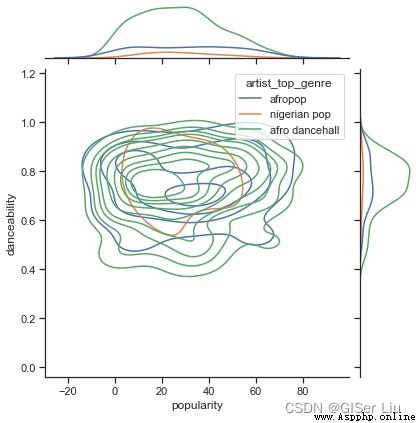
在數據探索階段我們可以自由去探尋不同特征之間的關系，如果你覺得繁瑣 你也可以用批處理函數來快速查看結果，盡管這樣少了很多趣味性。
從圖上看，這三種流派在人氣和可舞蹈性方面松散地對齊。 這說明我們對它進行聚類時將比較麻煩，數據差異太小。
我們繼續對這兩個特征創建散點圖查看數據分布。輸入以下代碼：
sns.FacetGrid(df, hue="artist_top_genre", size=5) \
.map(plt.scatter, "popularity", "danceability") \
.add_legend()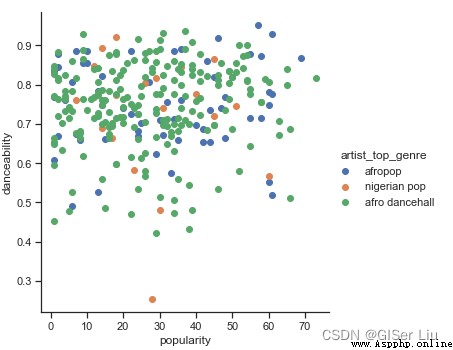
嗯哼，驗證了我們上面的猜想，數據分布很複雜，亂糟糟的。
對於聚類分析，我們通常可以使用散點圖來直觀地顯示數據聚類，掌握這種類型的可視化非常有用。
對於混亂的數據，我們可以使用箱型圖來直觀的查看數據的分布，從中找出異常數據並進行排除。輸入以下代碼查看不同數值型特征的箱型圖分布：
plt.figure(figsize=(20,20), dpi=200)
plt.subplot(4,3,1)#subplot函數劃分了4行3列的畫布區域，第三個參數錶示圖像在其中的比特置
sns.boxplot(x = 'popularity', data = df)
plt.subplot(4,3,2)
sns.boxplot(x = 'acousticness', data = df)
plt.subplot(4,3,3)
sns.boxplot(x = 'energy', data = df)
plt.subplot(4,3,4)
sns.boxplot(x = 'instrumentalness', data = df)
plt.subplot(4,3,5)
sns.boxplot(x = 'liveness', data = df)
plt.subplot(4,3,6)
sns.boxplot(x = 'loudness', data = df)
plt.subplot(4,3,7)
sns.boxplot(x = 'speechiness', data = df)
plt.subplot(4,3,8)
sns.boxplot(x = 'tempo', data = df)
plt.subplot(4,3,9)
sns.boxplot(x = 'time_signature', data = df)
plt.subplot(4,3,10)
sns.boxplot(x = 'danceability', data = df)
plt.subplot(4,3,11)
sns.boxplot(x = 'length', data = df)
plt.subplot(4,3,12)
sns.boxplot(x = 'release_date', data = df)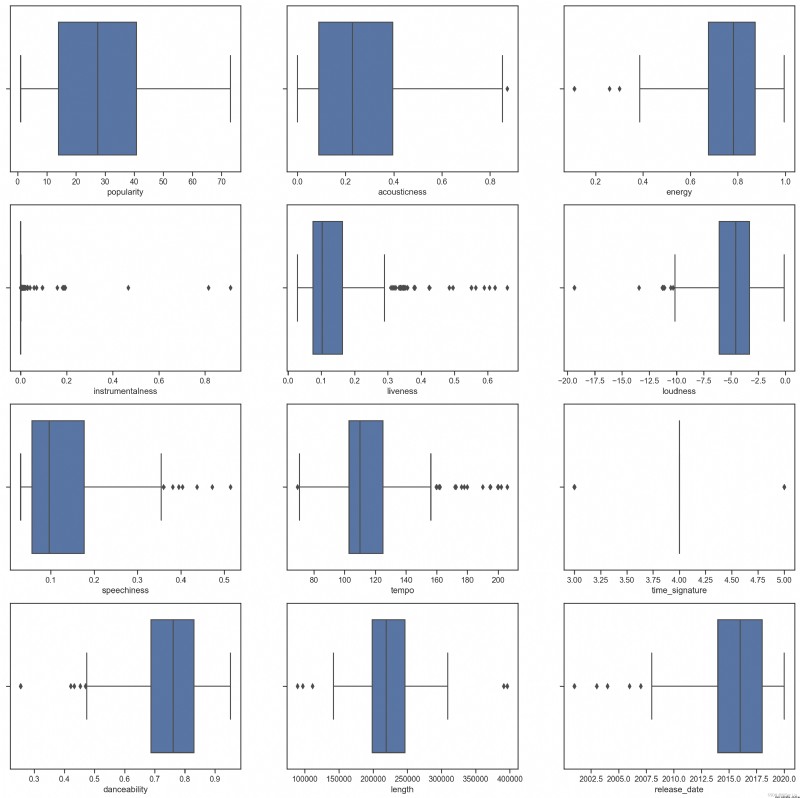
我們可以看到，*星號錶示異常值，箱體的比特置錶示數據的分布區域。圖中大量特征是分布不均勻的，異常值較多的樣本特征不適合聚類，我們可以對其進行進一步剔除。
現在，選擇將用於聚類分析練習的特征列。這些特征列需要具有相似的範圍；且其中的文本列數據需要編碼為數值數據：
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()#創建一個編碼器
X = df.loc[:,('artist_top_genre','popularity','danceability','acousticness','loudness','energy')]#loc為Selection by Label函數，即為按標簽取數據；將需要的標簽數據取出作為X訓練特征樣本
y = df['artist_top_genre']#將藝術家流派作為Y驗證模型精度標簽
X['artist_top_genre'] = le.fit_transform(X['artist_top_genre'])#對文本數據進行標簽化為數值格式
y = le.transform(y)#對文本數據進行標簽化為數值格式現在，我們需要選擇聚類的集群（簇）數量。我們已知可以從中取出3種歌曲類型，因此我們將nclusters賦值為3，輸入以下代碼：
from sklearn.cluster import KMeans
nclusters = 3 #初始化質心數量，因為我們想要劃分3中音樂類型，因此將其賦值為3
seed = 0 #選擇隨機初始化種子
km = KMeans(n_clusters=nclusters, random_state=seed)#一個random_state對應一個質心隨機初始化的隨機數種子。如果不指定隨機數種子，則 sklearn中的KMeans並不會只選擇一個隨機模式扔出結果
km.fit(X)#對Kmeans模型進行訓練
#使用訓練好的模型進行預測
y_cluster_kmeans = km.predict(X)
y_cluster_kmeans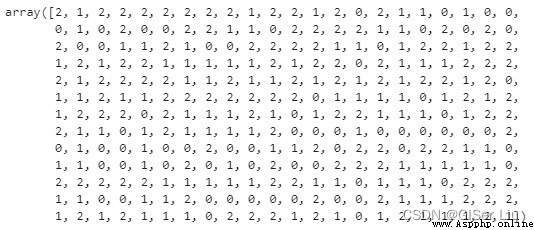
該數組即K-means模型的預測結果，其中數字為每行樣本的的聚類結果（0、1 或 2）。
我們接著使用此預測結果計算“輪廓系數”，輸入以下代碼：
from sklearn import metrics
score = metrics.silhouette_score(X, y_cluster_kmeans)# metrics.silhouette_score函數用於計算輪廓系數
score0 輪廓系數（Silhouette Coefficient），是聚類效果好壞的一種評價方式。
最佳值為1，最差值為-1。接近0的值錶示重疊的群集。負值通常錶示樣本已分配給錯誤的聚類，因為不同的聚類更為相似.
1 輪廓系數的公式為：S=(b-a)/max(a,b)，其中a是單個樣本離同類簇所有樣本的距離的平均數，b是單個樣本到不同簇所有樣本的平均。
輪廓系數錶示了同類樣本間距離最小化，不同類樣本間距離最大的度量
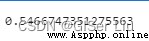
我們的模型輪廓系數是0.54，這錶明我們的數據不是特別適合這種類型的聚類，但這不影響我們的教學，實踐工作中總是有各種各樣的麻煩。我們接著進行訓練：
導入第三方庫，調整參數進行新一輪訓練，我們對簇的數量進行批處理，看看參數值為多少效果最佳：
from sklearn.cluster import KMeans
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
參數介紹：
0 range（）：這裏用for循環是為了迭代訓練輪數，這裏我們設置訓練10輪
1 random_state：確定初始化質心的隨機數生成。
2 wcss：用於存儲“聚類內平方和”測量聚類內所有點到聚類質心的平方平均距離。
3 inertia_：K-Means算法試圖選擇質心來最小化“慣性”，“衡量內部相幹聚類的尺度”。該值在每次迭代時都會追加到 wcss 變量中。這個評價參數錶示的是簇中某一點到簇中距離的和，這種方法雖然在評估參數最小時錶現了聚類的精細性
4 k-means++：在Scikit-learn中，你可以使用'k-means++'優化，它“初始化質心（通常情況下）彼此相距較遠，可能比隨機初始化有更好的結果。
我們使用lineplot函數繪制隨著類別（簇）數量的增加，inertia_參數值變化趨勢的折線圖。
plt.figure(figsize=(10,5))
sns.lineplot(range(1, 11), wcss,marker='o',color='red')
plt.title('Elbow')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()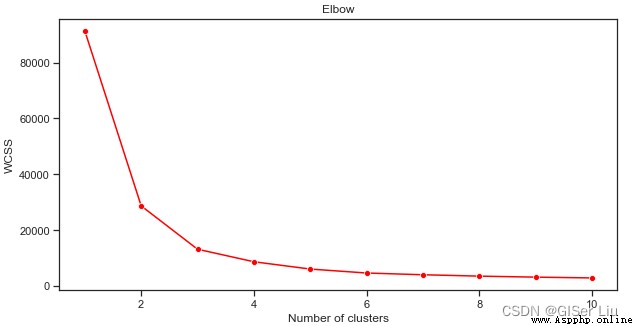
從這幅圖可以看出，K均值算法當簇數為3時，其inertia_參數效果較好，我們可以選擇3類或4類對數據集進行二次預測，評估其精度。
再次嘗試模型訓練與精度評價過程，這次設置3輪聚類，並將聚類結果以散點圖顯示：
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 3)#設置聚類的簇（類別）數量
kmeans.fit(X)#對模型進行訓練
labels = kmeans.predict(X)#輸出預測值
plt.scatter(df['popularity'],df['danceability'],c = labels)#以人氣為X軸，可舞蹈性為Y軸，標簽為類別繪制散點圖
plt.xlabel('popularity')
plt.ylabel('danceability')
plt.show()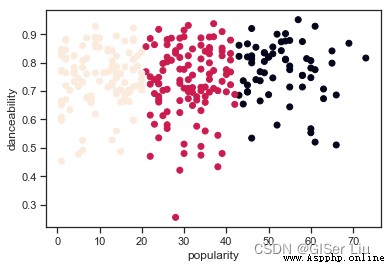
嗯？
輸入以下代碼檢查模型的准確度：
labels = kmeans.labels_#提取出模型中樣本的預測值labels
correct_labels = sum(y == labels)#統計預測正確的值
print("Result: %d out of %d samples were correctly labeled." % (correct_labels, y.size))
print('Accuracy score: {0:0.2f}'. format(correct_labels/float(y.size)))
可以看出，盡管我們調整了參數；所有樣本中，只有38%的樣本被成功預測了，換句話說，我們的K-means模型並不好。🤨但現實大部分情況就是這樣，分析的方法我已經交給你了，或許你可以選擇其他特征或其他的聚類模型來進一步提高模型的性能。
在本文中，我們學習了K-means算法的數學原理，作者以尼日利亞音樂數據集為案例。帶你了解了如何通過可視化的方式發現數據中潛在的特征。最後對訓練好的K-means模型進行了評估。
如果覺得我的文章對您有幫助，三連+關注便是對我創作的最大鼓勵！
“本站所有文章均為原創，歡迎轉載，請注明文章出處:https://blog.csdn.net/qq_45590504/category_11752103.html?spm=1001.2014.3001.5482百度和各類采集站皆不可信，搜索請謹慎鑒別。技術類文章一般都有時效性，本人習慣不定期對自己的博文進行修正和更新，因此請訪問出處以查看本文的最新版本。”
系列文章推薦
機器學習系列0 機器學習思想_GISer Liu的博客-CSDN博客
機器學習系列1 機器學習曆史_GISer Liu的博客-CSDN博客
機器學習系列2 機器學習的公平性_GISer Liu的博客-CSDN博客_公平機器學習
機器學習系列3 機器學習的流程_GISer Liu的博客-CSDN博客
機器學習系列4 使用Python創建Scikit-Learn回歸模型_GISer Liu的博客-CSDN博客
機器學習系列5 利用Scikit-learn構建回歸模型：准備和可視化數據（保姆級教程）_GISer Liu的博客-CSDN博客
機器學習系列6 使用Scikit-learn構建回歸模型：簡單線性回歸、多項式回歸與多元線性回歸_GISer Liu的博客-CSDN博客_多元多項式回歸機器學習系列7 基於Python的Scikit-learn庫構建邏輯回歸模型_GISer Liu的博客-CSDN博客機器學習系列8 基於Python構建Web應用以使用機器學習模型_GISer Liu的博客-CSDN博客
一文讀懂機器學習分類全流程_GISer Liu的博客-CSDN博客
基於Python構建機器學習Web應用_GISer Liu的博客-CSDN博客
