SVM(support vector machine)支持向量機:
注意:本文不准備提到數學證明的過程,一是因為有一篇非常好的文章解釋的非常好:支持向量機通俗導論(理解SVM的三層境界) ,另一方面是因為我只是個程序員,不是搞數學的(主要是因為數學不好。),主要目的是將SVM以最通俗易懂,簡單粗暴的方式解釋清楚。
線性分類:
先從線性可分的數據講起,如果需要分類的數據都是線性可分的,那麼只需要一根直線f(x)=wx+b就可以分開了,類似這樣:
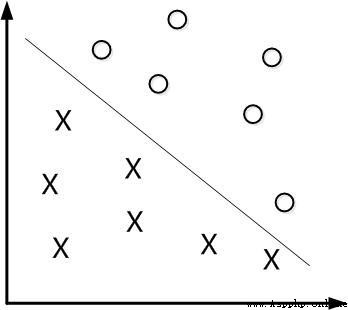
這種方法被稱為:線性分類器,一個線性分類器的學習目標便是要在n維的數據空間中找到一個超平面(hyper plane)。也就是說,數據不總是二維的,比如,三維的超平面是面。但是有個問題:
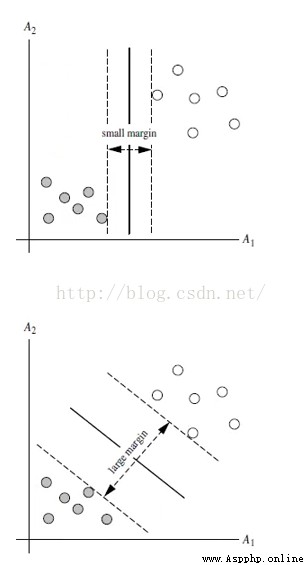
上述兩種超平面,都可以將數據進行分類,由此可推出,其實能有無數個超平面能將數據劃分,但是哪條最優呢?
最大間隔分類器Maximum Margin Classifier:
簡稱MMH, 對一個數據點進行分類,當超平面離數據點的“間隔”越大,分類的確信度(confidence)也越大。所以,為了使得分類的確信度盡量高,需要讓所選擇的超平面能夠最大化這個“間隔”值。這個間隔就是下圖中的Gap的一半。
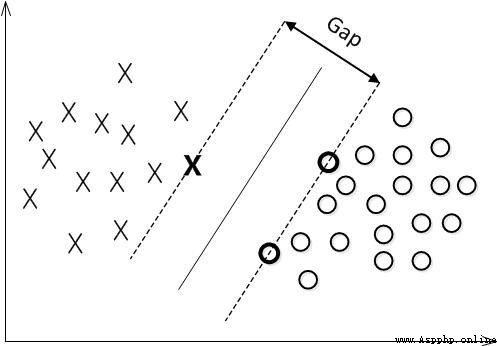
用以生成支持向量的點,如上圖XO,被稱為支持向量點,因此SVM有一個優點,就是即使有大量的數據,但是支持向量點是固定的,因此即使再次訓練大量數據,這個超平面也可能不會變化。
非線性分類:
數據大多數情況都不可能是線性的,那如何分割非線性數據呢?
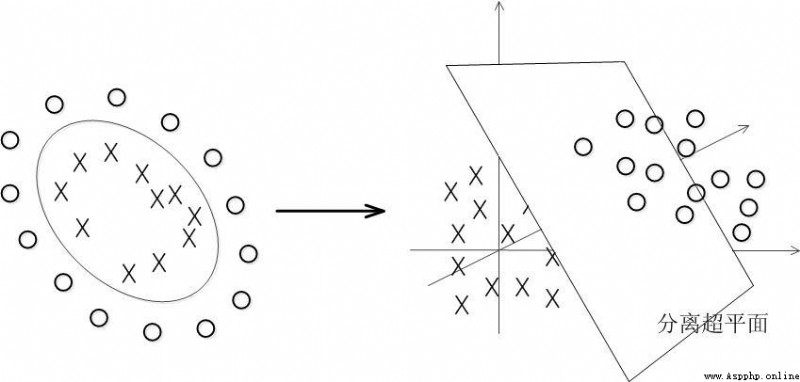
解決方法是將數據放到高維度上再進行分割,如下圖:
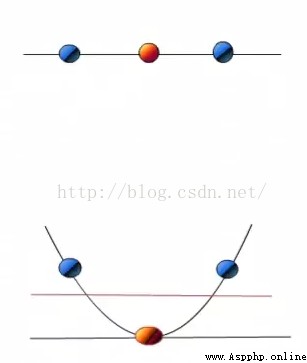
當f(x)=x時,這組數據是個直線,如上半部分,但是當我把這組數據變為f(x)=x^2時,這組數據就變成了下半部分的樣子,也就可以被紅線所分割。
比如說,我這裡有一組三維的數據X=(x1,x2,x3),線性不可分割,因此我需要將他轉換到六維空間去。因此我們可以假設六個維度分別是:x1,x2,x3,x1^2,x1*x2,x1*x3,當然還能繼續展開,但是六維的話這樣就足夠了。
新的決策超平面:d(Z)=WZ+b,解出W和b後帶入方程,因此這組數據的超平面應該是:d(Z)=w1x1+w2x2+w3x3+w4*x1^2+w5x1x2+w6x1x3+b但是又有個新問題,轉換高緯度一般是以內積(dot product)的方式進行的,但是內積的算法復雜度非常大。
核函數Kernel:
我們會經常遇到線性不可分的樣例,此時,我們的常用做法是把樣例特征映射到高維空間中去。但進一步,如果凡是遇到線性不可分的樣例,一律映射到高維空間,那麼這個維度大小是會高到可怕的,而且內積方式復雜度太大。此時,核函數就隆重登場了,核函數的價值在於它雖然也是講特征進行從低維到高維的轉換,但核函數絕就絕在它事先在低維上進行計算,而將實質上的分類效果表現在了高維上,也就如上文所說的避免了直接在高維空間中的復雜計算。
幾種常用核函數:
h度多項式核函數(Polynomial Kernel of Degree h)
高斯徑向基和函數(Gaussian radial basis function Kernel)
S型核函數(Sigmoid function Kernel)
圖像分類,通常使用高斯徑向基和函數,因為分類較為平滑,文字不適用高斯徑向基和函數。沒有標准的答案,可以嘗試各種核函數,根據精確度判定。
松弛變量:
數據本身可能有噪點,會使得原本線性可分的數據需要映射到高維度去。對於這種偏離正常位置很遠的數據點,我們稱之為 outlier ,在我們原來的 SVM 模型裡,outlier 的存在有可能造成很大的影響,因為超平面本身就是只有少數幾個 support vector 組成的,如果這些 support vector 裡又存在 outlier 的話,其影響就很大了。
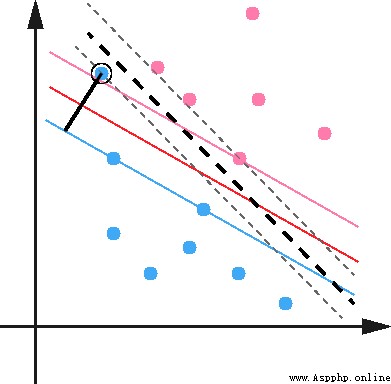
因此排除outlier點,可以相應的提高模型准確率和避免Overfitting的方式。
解決多分類問題:
經典的SVM只給出了二類分類的算法,現實中數據可能需要解決多類的分類問題。因此可以多次運行SVM,產生多個超平面,如需要分類1-10種產品,首先找到1和2-10的超平面,再尋找2和1,3-10的超平面,以此類推,最後需要測試數據時,按照相應的距離或者分布判定。
SVM與其他機器學習算法對比(圖):
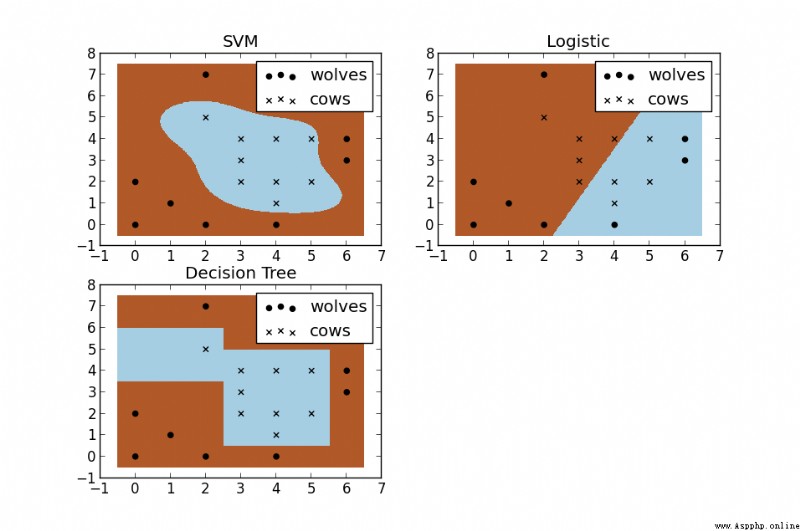
Python實現方式:
線性,基礎:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
fromsklearn importsvm
x =[[2,0,1],[1,1,2],[2,3,3]]
y =[0,0,1] #分類標記
clf =svm.SVC(kernel ='linear') #SVM模塊,svc,線性核函數
clf.fit(x,y)
print(clf)
print(clf.support_vectors_) #支持向量點
print(clf.support_) #支持向量點的索引
print(clf.n_support_) #每個class有幾個支持向量點
print(clf.predict([2,0,3])) #預測
線性,展示圖:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
fromsklearn importsvm
importnumpy as np
importmatplotlib.pyplot as plt
np.random.seed(0)
x =np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]] #正態分布來產生數字,20行2列*2
y =[0]*20+[1]*20#20個class0,20個class1
clf =svm.SVC(kernel='linear')
clf.fit(x,y)
w =clf.coef_[0] #獲取w
a =-w[0]/w[1] #斜率
#畫圖劃線
xx =np.linspace(-5,5) #(-5,5)之間x的值
yy =a*xx-(clf.intercept_[0])/w[1] #xx帶入y,截距
#畫出與點相切的線
b =clf.support_vectors_[0]
yy_down =a*xx+(b[1]-a*b[0])
b =clf.support_vectors_[-1]
yy_up =a*xx+(b[1]-a*b[0])
print("W:",w)
print("a:",a)
print("support_vectors_:",clf.support_vectors_)
print("clf.coef_:",clf.coef_)
plt.figure(figsize=(8,4))
plt.plot(xx,yy)
plt.plot(xx,yy_down)
plt.plot(xx,yy_up)
plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=80)
plt.scatter(x[:,0],x[:,1],c=y,cmap=plt.cm.Paired) #[:,0]列切片,第0列
plt.axis('tight')
plt.show()
文章來源:https://www.jb51.net/article/131580.htm