SVM(support vector machine) Support vector machine :
Be careful : This article is not going to mention the process of mathematical proof , One is that there is a very good article that explains it very well : General introduction to support vector machines ( understand SVM Three levels of state ) , On the other hand, I am just a programmer , Not a math guy ( It's mainly because math is not good .), The main purpose is to SVM In the most accessible , Explain clearly in a simple and crude way .
Linear classification :
Let's start with linearly separable data , If the data to be classified are linearly separable , Then you just need a straight line f(x)=wx+b You can separate , Like this :
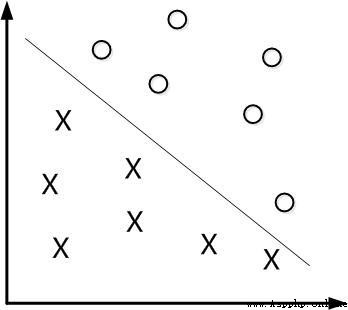
This method is called : Linear classifier , The learning goal of a linear classifier is to n Find a hyperplane in the data space of dimension (hyper plane). in other words , Data is not always two-dimensional , such as , A three-dimensional hyperplane is a face . But there's a problem :
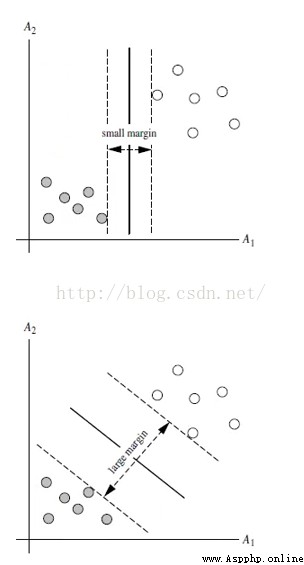
These two hyperplanes , Can classify the data , From this, we can deduce , In fact, there can be countless hyperplanes that can divide the data , But which is the best ?
Maximum interval classifier Maximum Margin Classifier:
abbreviation MMH, Classify a data point , When the hyperplane is away from the data point “ interval ” The bigger it is , Certainty of classification (confidence) The greater the . therefore , In order to make the classification as sure as possible , We need to maximize this by choosing a hyperplane “ interval ” value . This interval is shown below Gap Half of .
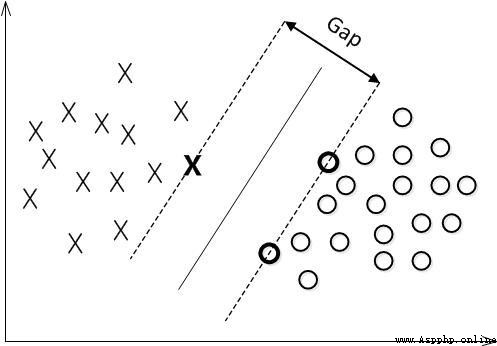
The point used to generate the support vector , Pictured above XO, Called support vector points , therefore SVM There is an advantage , Even if there is a lot of data , But support vector points are fixed , So even if you train a lot of data again , This hyperplane may not change .
Nonlinear classification :
Data can't be linear in most cases , How to segment non-linear data ?
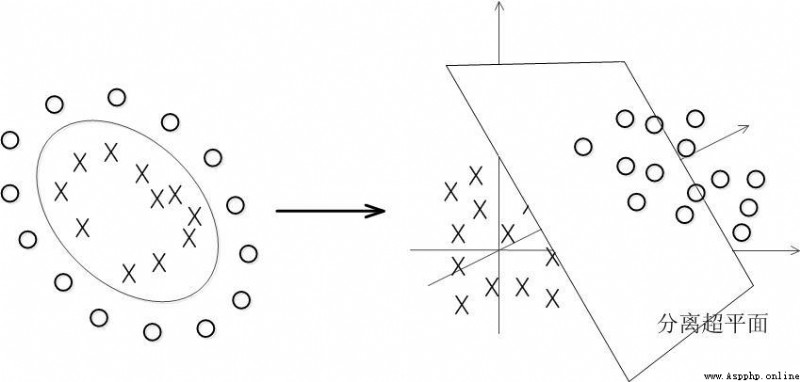
The solution is to put the data on a high dimension and then split it , Here's the picture :
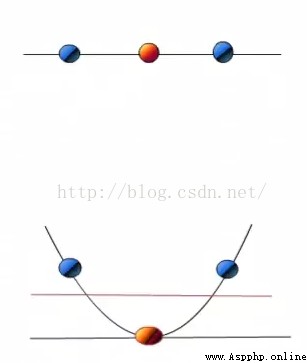
When f(x)=x when , This set of data is a straight line , The upper half , But when I turn this set of data into f(x)=x^2 when , This set of data becomes the lower part , It can be divided by the red line .
for instance , I have a set of three-dimensional data here X=(x1,x2,x3), Linear indivisible , So I need to convert it to six-dimensional space . So we can assume that the six dimensions are :x1,x2,x3,x1^2,x1*x2,x1*x3, Of course, it can continue to unfold , But in six dimensions, that's enough .
New decision hyperplane :d(Z)=WZ+b, figure out W and b Then bring it into the equation , Therefore, the hyperplane of this set of data should be :d(Z)=w1x1+w2x2+w3x3+w4*x1^2+w5x1x2+w6x1x3+b But there is a new problem , The conversion of high latitude is generally based on inner product (dot product) In the way of , But the algorithm complexity of inner product is very large .
Kernel function Kernel:
We often encounter examples of linear indivisibility , here , Our common practice is to map sample features to high-dimensional space . But further , If we encounter linear indivisible examples , All map to high dimensional space , So the dimension size is going to be terrible , And the inner product method is too complicated . here , The kernel function is on the stage , The value of kernel function is that although it is also about feature transformation from low dimension to high dimension , But the kernel function must be calculated in the low dimension in advance , And the classification effect in essence is shown in the high dimension , As mentioned above, the complex computation directly in high-dimensional space is avoided .
Several common kernel functions :
h Degree polynomial kernel function (Polynomial Kernel of Degree h)
Gaussian radial basis and function (Gaussian radial basis function Kernel)
S Type kernel function (Sigmoid function Kernel)
Image classification , Gaussian radial basis functions and , Because the classification is smoother , Text does not apply to Gaussian radial basis functions . There is no standard answer , You can try various kernel functions , Judge according to the accuracy .
Relax variables :
The data itself may have noise , It will make the originally linearly separable data need to be mapped to high dimensions . For this kind of data point far away from the normal position , We call it outlier , In our original SVM In the model ,outlier The existence of the can have a big impact , Because the hyperplane itself is just a few support vector Composed of , If these support vector There's... In it outlier Words , The impact is great .
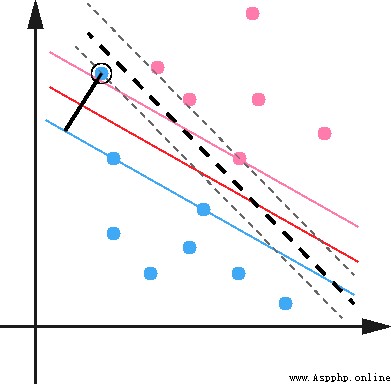
Thus eliminate outlier spot , It can improve the accuracy of the model and avoid Overfitting The way .
Solve the problem of multi classification :
classical SVM Only two kinds of classification algorithms are given , In reality, data may need to solve the problem of multi class classification . So it can be run many times SVM, Generate multiple hyperplanes , If classification is required 1-10 Products , First find 1 and 2-10 The hyperplane of , Search again 2 and 1,3-10 The hyperplane of , And so on , Finally, when you need to test data , According to the corresponding distance or distribution .
SVM Compared with other machine learning algorithms ( chart ):
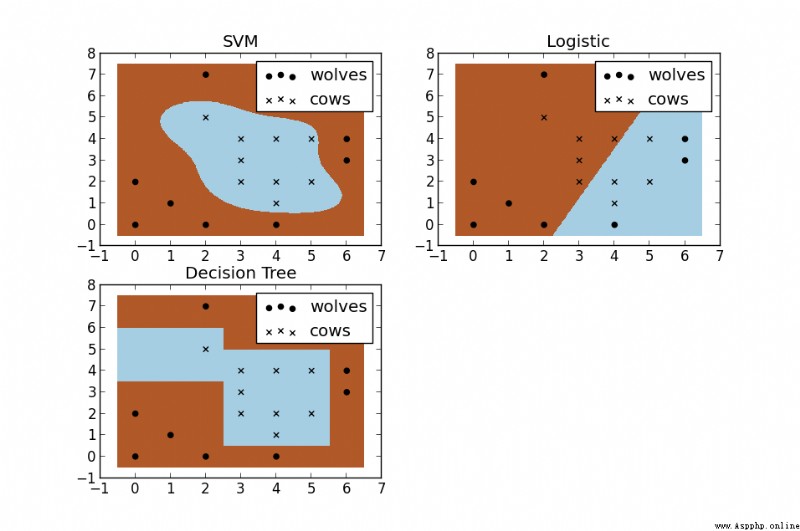
Python Realization way :
linear , Basics :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
fromsklearn importsvm
x =[[2,0,1],[1,1,2],[2,3,3]]
y =[0,0,1] # Classification marks
clf =svm.SVC(kernel ='linear') #SVM modular ,svc, Linear kernel function
clf.fit(x,y)
print(clf)
print(clf.support_vectors_) # Support vector points
print(clf.support_) # Index of support vector points
print(clf.n_support_) # Every class There are several support vector points
print(clf.predict([2,0,3])) # forecast
linear , Show pictures :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
fromsklearn importsvm
importnumpy as np
importmatplotlib.pyplot as plt
np.random.seed(0)
x =np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]] # Normal distribution to produce numbers ,20 That's ok 2 Column *2
y =[0]*20+[1]*20#20 individual class0,20 individual class1
clf =svm.SVC(kernel='linear')
clf.fit(x,y)
w =clf.coef_[0] # obtain w
a =-w[0]/w[1] # Slope
# Draw a line
xx =np.linspace(-5,5) #(-5,5) Between x Value
yy =a*xx-(clf.intercept_[0])/w[1] #xx Into the y, intercept
# Draw a line tangent to the point
b =clf.support_vectors_[0]
yy_down =a*xx+(b[1]-a*b[0])
b =clf.support_vectors_[-1]
yy_up =a*xx+(b[1]-a*b[0])
print("W:",w)
print("a:",a)
print("support_vectors_:",clf.support_vectors_)
print("clf.coef_:",clf.coef_)
plt.figure(figsize=(8,4))
plt.plot(xx,yy)
plt.plot(xx,yy_down)
plt.plot(xx,yy_up)
plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=80)
plt.scatter(x[:,0],x[:,1],c=y,cmap=plt.cm.Paired) #[:,0] Column slice , The first 0 Column
plt.axis('tight')
plt.show()
Source of the article :https://www.jb51.net/article/131580.htm