考試好難......先把會的題寫一下，不會的有緣再寫
【問題描述】
斐波那契數列的遞推公式為：Fn = Fn-1＋ Fn-2，其中F1= F2 = 1。
請問，斐波那契數列的第 1 至 202202011200 項(含)中，有多少項的個位是 7。
【解析及代碼】
這道題的運算次數大約是 1e11，而 Python 每秒可以進行的運算次數大約是 8e7，暴力的話可能需要十幾分鐘
求解斐波那契數列，比較傳統的方法是遞歸，但是遞歸很容易爆棧，所以建議 for 循環解決
找到循環一切都好辦，答案：26960268160
num = 202202011200
f1 = f2 = 1
# 個位列表
cycle = [1, 1]
for i in range(3, num):
# 斐波那契數列遞進
f1, f2 = f2, f1 + f2
# 求出個位
f2 %= 10
cycle.append(f2)
# 查找循環
if cycle[-2:] == cycle[:2]: break
# 除去末兩位
cycle = cycle[:-2]
print(cycle)
# 循環的長度
cycle_len = len(cycle)
count_7 = cycle.count(7)
# num 剛好可被 60 整除
print(num % cycle_len)
result = num // cycle_len * count_7
# 26960268160
print(result)【問題描述】
小藍很喜歡科研，他最近做了一個實驗得到了一批實驗數據，一共是兩百萬個正整數。如果按照預期，所有的實驗數據 x 都應該滿足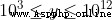 
。但是做實驗都會有一些誤差，會導致出現一些預期外的數據，這種誤差數據 y 的范圍是 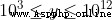。由於小藍做實驗很可靠，所以他所有的實驗數據中 99.99% 以上都是符合預期的。小藍的所有實驗數據都在 primes.txt 中，現在他想統計這兩百萬個正整數中有多少個是質數，你能告訴他嗎?
【解析及代碼】
羅裡吧嗦一堆其實就是找出一個文件裡面有多少個數是質數，因為數字不大，用試除法就可以解決
當給定數字 n 的時候，如果 n 是合數，那麼 n 必然可被 [2,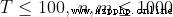 
] 內的某一整數整除，從而可以寫出判質函數
使用 open 函數讀取 txt 文件，對每一行的數字進行判斷，並輸出進度信息
答案：342693
from math import isqrt
def try_divide(n):
''' 試除法'''
if n <= 3: return n in [2, 3]
bound = isqrt(n)
for i in range(2, bound + 1):
if n % i == 0: return False
return True
cnt = 0
with open('primes.txt') as f:
lines = list(f.readlines())
for cur, i in enumerate(lines):
# 除去換行符
i = int(i.strip())
if try_divide(i): cnt += 1
# 輸出進度
print(f'\r{(cur + 1) / len(lines) * 100:.2f} %', end='')
print()
# 342693
print(cnt)【問題描述】
給定 n,m，問是否存在兩個不同的數 x,y 使得 1 ≤ x < y ≤ m 且 n mod x = n mod y
【輸入格式】
輸入包含多組獨立的詢問。
第一行包含一個整數 T 表示詢問的組數。
接下來 T 行每行包含兩個整數 n,m，用一個空格分隔，表示一組詢問。
【輸出格式】
輸出 T 行，每行依次對應一組詢問的結果。如果存在，輸出單詞 Yes；如果不存在，輸出單詞 No
【樣例】
輸入輸出3
1 2
5 2
999 99
【評測用例規模與約定】
20%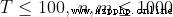50%
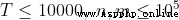100%
【解析及代碼】
【問題描述】
小藍最近總喜歡計算自己的代碼中定義的變量占用了多少內存空間。為了簡化問題，變量的類型只有以下三種:
int：整型變量，一個 int 型變量占用 4 Byte 的內存空間。
long：長整型變量，一個long型變量占用8 Byte 的內存空間。
string：字符串變量，占用空間和字符串長度有關，設字符串長度為 L，則字符串占用 L Byte 的內存空間，如果字符串長度為 0 則占用 0 Byte 的內存空間。
定義變量的語句只有兩種形式，第一種形式為:
type var1=value1,var2=value2…;
定義了若干個 type 類型變量 var1、var2、…，並且用 value1、value2… 初始化，多個變量之間用 ',’ 分隔，語句以 ';’ 結尾，type可能是int、long 或string。例如 int a=1,b=5,c=6; 占用空間為12 Byte；long a=1,b=5;占用空間為16 Byte；String s1="",s2="hello",s3="world";占用空間為10 Byte
第二種形式為：
type[] arr1=new type[size1],arr2=new type[size2]…；
定義了若干 type 類型的一維數組變量 arr1、arr2…，且數組的大小為 size1、size2…，多個變量之間用 ',' 進行分隔，語句以 ';' 結尾，type 只可能是 int 或 long。例如int[] a1=new int[10];占用的內存空間為 40 Byte；long[] a1=new long[10],a2=new long[10];占用的內存空間為 160 Byte。
已知小藍有 T 條定義變量的語句，請你幫他統計下一共占用了多少內存空間。結果的表示方式為：aGBbMBcKBdB，其中 a、b、c、d 為統計的結果，GB、MB、KB、B為單位。優先用大的單位來表示，1GB=1024MB，1MB=1024KB，1KB=1024B，其中 B 表示 Byte。如果 a、b、c、d 中的某幾個數字為 0，那麼不必輸出這幾個數字及其單位。題目保證一行中只有一句定義變量的語句，且每條語句都滿足題干中描述的定義格式，所有的變量名都是合法的且均不重復。題目中的數據很規整，和上述給出的例子類似，除了類型後面有一個空格，以及定義數組時 new 後面的一個空格之外，不會出現多余的空格。
【輸入格式】
輸入的第一行包含一個整數 T，表示有 T 句變量定義的語句。接下來 T 行，每行包含一句變量定義語句
【輸出格式】
輸出一行包含一個字符串，表示所有語句所占用空間的總大小
【樣例】
輸入輸出1【評測用例規模與約定】
對於所有評測用例，1 ≤ T ≤ 10，每條變量定義語句的長度不會超過 1000。所有的變量名稱長度不會超過 10，且都由小寫字母和數字組成。對於整型變量，初始化的值均是在其表示范圍內的十進制整數，初始化的值不會是變量。對於 String 類型的變量，初始化的內容長度不會超過 50，且內容僅包含小寫字母和數字，初始化的值不會是變量。對於數組類型變量，數組的長度為一個整數，范圍為：[0, 2^30]，數組的長度不會是變量。T 條語句定義的變量所占的內存空間總大小不會超過 1 GB，且大於 0 B。
【解析及代碼】
思路就是暴力，使用 re 正則表達式進行字符串匹配，算得內存空間總數：
import re
space = {'int': 4, 'long': 8}
byte = 0
for _ in range(int(input())):
sentence = input().rstrip(';').split()
type_ = sentence.pop(0)
# 如果是數組
if type_[-2:] == '[]':
type_ = type_[:-2]
# 取出語句塊進行統計
for token in sentence:
find = re.search(r'\[[0-9]+]', token)
if find:
find = int(find.group()[1:-1])
byte += space[type_] * find
# 如果是普通變量
else:
sentence = sentence[0].split(',')
# 字符類型需要看字符串的長度
if type_ == 'String':
for token in sentence:
find = re.search(r'=.*', token)
if find:
find = find.group()
# 除去雙引號、等號
# 長度即為 bytes
byte += len(find[2: -1])
else:
# sentence 多長就有多少個變量
byte += len(sentence) * space[type_]使用字典記錄每個單位對應的數值，將總內存空間換算後寫入，使用 for 循環輸出
BASE = 2 ** 10
result = {unit: 0 for unit in ('GB', 'MB', 'KB', 'B')}
# 計算 GB
result['GB'] = byte // BASE ** 3
byte -= BASE ** 3 * result['GB']
# 計算 MB
result['MB'] = byte // BASE ** 2
byte -= BASE ** 2 * result['MB']
# 計算 KB
result['KB'] = byte // BASE
byte -= BASE * result['KB']
# 記錄 B
result['B'] = byte
final = ''
for unit in result:
value = result[unit]
if value:
final += f'{value}{unit}'
print(final)【問題描述】
小藍有一個長度為 n 的數組 A = (a1, a2, · · · , an)，數組的子數組被定義為從原數組中選出連續的一個或多個元素組成的數組。數組的最大公約數指的是數組中所有元素的最大公約數。如果最多更改數組中的一個元素之後，數組的最大公約數為 g，那麼稱 g 為這個數組的近似 GCD。一個數組的近似 GCD 可能有多種取值。具體的，判斷 g 是否為一個子數組的近似 GCD 如下：
1. 如果這個子數組的最大公約數就是 g，那麼說明 g 是其近似 GCD。
2. 在修改這個子數組中的一個元素之後（可以改成想要的任何值），子數組的最大公約數為 g，那麼說明 g 是這個子數組的近似 GCD。
小藍想知道，數組 A 有多少個長度大於等於 2 的子數組滿足近似 GCD 的值為 g
【輸入格式】
輸入的第一行包含兩個整數 n, g，用一個空格分隔，分別表示數組 A 的長度和 g 的值。
第二行包含 n 個整數 a1, a2, · · · , an，相鄰兩個整數之間用一個空格分隔。
【輸出格式】
輸出一行包含一個整數表示數組 A 有多少個長度大於等於 2 的子數組的近似 GCD 的值為 g
【樣例】
輸入輸出說明5 3【評測用例規模與約定】
20%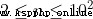
40%
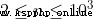100%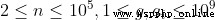
【解析及代碼】
近似公約數的規律如下：
枚舉區間左邊界，位於左邊界上的數作為初始的最大公約數 last_gcd：
再枚舉區間的右邊界：
from math import gcd
length, g = map(int, input().split())
array = list(map(int, input().split()))
cnt = 0
# 枚舉左邊界
for left in range(length):
# 當前的最大公約數
last_gcd = array[left]
if last_gcd % g == 0:
is_change = False
else:
last_gcd = g
is_change = True
# 枚舉右邊界
for right in range(left + 1, length):
cur_gcd = gcd(last_gcd, array[right])
# 如果當前 gcd 可被 g 整除, 隨便修改一個數為 g 便可以
if cur_gcd % g == 0:
cnt += 1
elif not is_change:
# 只修改當前位置上的數為 g
cur_gcd = gcd(last_gcd, g)
is_change = True
if cur_gcd == g:
cnt += 1
else:
break
last_gcd = cur_gcd
print(cnt)【問題描述】
LQ 市的交通系統可以看成由 n 個結點和 m 條有向邊組成的有向圖。在每條邊上有一個信號燈，會不斷按綠黃紅黃綠黃紅黃... 的順序循環 (初始時剛好變到綠燈)。當信號燈為綠燈時允許正向通行，紅燈時允許反向通行，黃燈時不允許通行。每條邊上的信號燈的三種顏色的持續時長都互相獨立，其中黃燈的持續時長等同於走完路徑的耗時。當走到一條邊上時，需要觀察邊上的信號燈，
如果允許通行則可以通過此邊，在通行過程中不再受信號燈的影響；否則需要等待，直到允許通行。
請問從結點 s 到結點 t 所需的最短時間是多少，如果 s 無法到達 t 則輸出 −1
【輸入格式】
輸入的第一行包含四個整數 n, m, s, t，相鄰兩個整數之間用一個空格分隔。
接下來 m 行，每行包含五個整數 ui, vi, gi,ri, di ，相鄰兩個整數之間用一個空格分隔，分別表示一條邊的起點，終點，綠燈、紅燈的持續時長和距離（黃燈的持續時長）。
【輸出格式】
輸出一行包含一個整數表示從結點 s 到達 t 所需的最短時間
【樣例】
輸入輸出4 4 1 4【評測用例規模與約定】
40%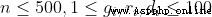
70%
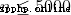100%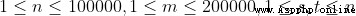
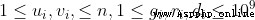
【解析及代碼】
【問題描述】
小藍最近迷上了一款名為《點亮》的謎題游戲，游戲在一個 n × n 的格子棋盤上進行，棋盤由黑色和白色兩種格子組成，玩家在白色格子上放置燈泡，確保任意兩個燈泡不會相互照射，直到整個棋盤上的白色格子都被點亮（每個謎題均為唯一解）。燈泡只會往水平和垂直方向發射光線，照亮整行和整列，除非它的光線被黑色格子擋住。黑色格子上可能有從 0 到 4 的整數數字，表示與其上下左右四個相鄰的白色格子共有幾個燈泡；也可能沒有數字，這表示可以在上下左右四個相鄰的白色格子處任意選擇幾個位置放置燈泡。游戲的目標是選擇合適的位置放置燈泡，使得整個棋盤上的白色格子都被照亮。
例如，有一個黑色格子處數字為 4，這表示它周圍必須有 4 個燈泡，需要在他的上、下、左、右處分別放置一個燈泡；如果一個黑色格子處數字為 2，它的上下左右相鄰格子只有 3 個格子是白色格子，那麼需要從這三個白色格子中選擇兩個來放置燈泡；如果一個黑色格子沒有標記數字，且其上下左右相鄰格子全是白色格子，那麼可以從這 4 個白色格子中任選出 0 至 4 個來放置燈泡。
題目保證給出的數據是合法的，黑色格子周圍一定有位置可以放下對應數量的燈泡。且保證所有謎題的解都是唯一的。
現在，給出一個初始的棋盤局面，請在上面放置好燈泡，使得整個棋盤上的白色格子被點亮。
【輸入格式】
輸入的第一行包含一個整數 n，表示棋盤的大小。
接下來 n 行，每行包含 n 個字符，表示給定的棋盤。字符 . 表示對應的格子為白色，數字字符 0、1、2、3、4 表示一個有數字標識的黑色格子，大寫字母 X 表示沒有數字標識的黑色格子。
【輸出格式】
輸出 n 行，每行包含 n 個字符，表示答案。大寫字母 O 表示對應的格子包含燈泡，其它字符的意義與輸入相同
【樣例】
輸入輸出說明5
【評測用例規模與約定】
100%2 ≤ n ≤ 5 ，且棋盤上至少有 15% 的格子是黑色格子【解析及代碼】
【問題描述】
小藍打算采購 n 種物品，每種物品各需要 1 個。
小藍所住的位置附近一共有 m 個店鋪，每個店鋪都出售著各種各樣的物品。
第 i 家店鋪會在第 si 天至第 ti 天打折，折扣率為 pi，對於原件為 b 的物品，折後價格為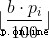 
。其它時間需按原價購買。
小藍很忙，他只能選擇一天的時間去采購這些物品。請問，他最少需要花多少錢才能買到需要的所有物品。
題目保證小藍一定能買到需要的所有物品。
【輸入格式】
輸入的第一行包含兩個整數 n, m，用一個空格分隔，分別表示物品的個數和店鋪的個數。
接下來依次包含每個店鋪的描述。每個店鋪由若干行組成，其中第一行包含四個整數 si, ti, pi, ci，相鄰兩個整數之間用一個空格分隔，分別表示商店優惠的起始和結束時間、折扣率以及商店內的商品總數。之後接 ci 行，每行包含兩個整數 aj, bj ，用一個空格分隔，分別表示該商店的第 j 個商品的類型和價格。商品的類型由 1 至 n 編號。
【輸出格式】
輸出一行包含一個整數表示小藍需要花費的最少的錢數
【樣例】
輸入輸出2 2
1 2 89 1
1 97
3 4 77 1
2 15
【評測用例規模與約定】
40%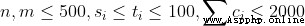
70%
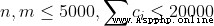100%
【解析及代碼】
【問題描述】
小藍很喜歡 owo ，他現在有一些字符串，他想將這些字符串拼接起來，使得最終得到的字符串中出現盡可能多的 owo 。
在計算數量時，允許字符重疊，即 owowo 計算為 2 個，owowowo 計算為 3 個。
請算出最優情況下得到的字符串中有多少個 owo。
【輸入格式】
輸入的第一行包含一個整數 n ，表示小藍擁有的字符串的數量。
接下來 n 行，每行包含一個由小寫英文字母組成的字符串 si 。
【輸出格式】
輸出 n 行，每行包含一個整數，表示前 i 個字符串在最優拼接方案中可以得到的 owo 的數量
【樣例】
輸入輸出31
1
2
【評測用例規模與約定】
10%n ≤ 1040%n ≤ 30060%n ≤ 5000100%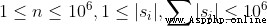
【解析及代碼】
【問題描述】
給定一個僅含小寫英文字母的字符串 s，每次操作選擇一個區間 [li,ri] 將 s 的該區間中的所有字母 xi 全部替換成字母 yi，問所有操作做完後，得到的字符串是什麼。
【輸入格式】
輸入的第一行包含一個字符串 s 。
第二行包含一個整數 m 。
接下來 m 行，每行包含 4 個參數 li,ri, xi, yi，相鄰兩個參數之間用一個空格分隔，其中 li,ri 為整數，xi, yi 為小寫字母。
【輸出格式】
輸出一行包含一個字符串表示答案
【樣例】
輸入輸出abcaaea【評測用例規模與約定】
40%
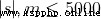100%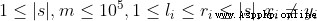
【解析及代碼】
這個題這麼簡單放在壓軸區我就很不理解 —— 還 25 分，我都沒有給這個題預留時間，看到的時候已經來不及做了
因為字符串是沒辦法原地修改的，所以使用切片表達式切成三段，對中間段進行字符替換，再進行拼接操作
string = input()
for _ in range(int(input())):
l, r, old, new = input().split()
l, r = map(lambda i: int(i) - 1, [l, r])
l_part, mid_part, r_part = string[:l], string[l: r + 1], string[r + 1:]
string = ''.join([l_part, mid_part.replace(old, new), r_part])
print(string)
