我估計省賽 48.5 分左右 (滿分 150)。廣東總共 78 個省一,我只排到了第 33 (42.3%)

在本篇文章中,我將從“知識預備”、“刷題網站”、“函數模板”三個方面為大家講解怎樣准備藍橋杯 Python 組的比賽
如果你們進入了國賽,想統計省一的人數,可以看我這篇文章:藍橋杯 省一人數統計 Python 實現
不會改正則表達式的話在評論區留言,我會幫你們統計的 ~
官方要求的是 IDLE,但是就今年來說,是可以用 PyCharm 的(具體還是要問清楚)
用 PyCharm 的話自己配好 3.8.6 的環境就可以

我主要看了這個網課的前 40 集,因為專業課學了樹、圖,所以重點放在了動態規劃、背包、狀態壓縮、線段樹
【藍橋杯比賽】視頻教程(入門學習+算法輔導) https://www.bilibili.com/video/BV1Lb4y1k7K3?
https://www.bilibili.com/video/BV1Lb4y1k7K3?
貪心算法的話,比較玄學,練習為主:LeetCode:貪心算法題集
還有數論、計算幾何、前綴和、差分都是考點,但是我沒有好的網課推薦
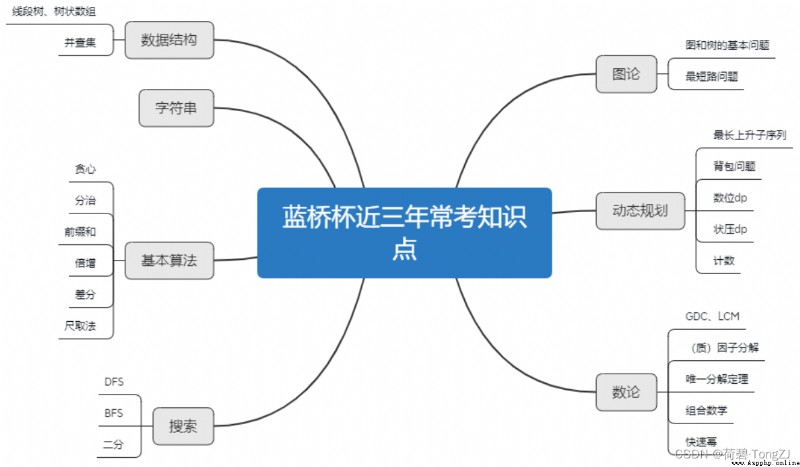
借用藍橋雲課的思維導圖 ~
然後比賽答題時,一定要先看所有題的題目,因為題目的難度不一定是遞增的 —— 要知道我今年看見全卷最簡單的題在最後、還沒時間做了有多絕望
學標准庫之前,首先還得會 Python 的一些基礎數據結構(列表、元組、字典、字符串……)
而且對於類和實例的認識是越深越好(如類似 __call__ 這種名字的類函數),這有利於你直接閱讀源代碼,提高對標准庫的認知
一般情況下,標准庫函數的性能是最好的,所以能用一定要用
對於 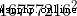 ,Python 1 秒內可以進行 8e7 次運算(加法亦然),解題時根據問題規模設計好代碼的時間復雜度
,Python 1 秒內可以進行 8e7 次運算(加法亦然),解題時根據問題規模設計好代碼的時間復雜度
對於有序數列,二分法查找的速度會快很多
升序
bisect_left(array, x)
二分法查找x的位置
insort(array, x)
二分法插入x
數值操作:
pi
п
isnan(z)
判斷nan
isinf(z)
判斷inf
isfinite(z)
是否有限
tau
2п
nan
nan
inf
∞
isclose(a, b)
是否相近
cmath 庫是復數運算庫,在藍橋杯比賽裡面很實用
藍橋杯經常出現一些 x-y 坐標系求兩點間距離、角度的題,利用復數的模、相角求解可以簡化代碼和提高運算速度
屬性訪問:
z.real
復數實部
z.imag
復數虛部
abs(z)
復數的模
phase(z)
復數相角 (-п, п]
z.conjugate()
對應共轭復數
rect(r, phi)
極坐標 -> 復數
polar(z)
復數 -> 極坐標 (r, φ)
這個庫主要提供了計數器,可快速統計序列(如字符串)中的元素
計數器:
Counter(var / **kwargs)
返回計數器
CNT.elements()
返回元素迭代器
CNT.most_common(int)
返回指定數量高頻值
CNT.update(var)
更新計數器
加法
CNT.subtract(var)
減法
藍橋杯有時會有一些關於日期的題,這個庫配合 try - except 語句可以判斷某個日期的合法性
time 庫的話就沒什麼必要了,不如這個庫快捷;了解下 time 庫的浮點型秒數、strptime 方法就可以
日期時間:
datetime(year, month, day, hour=0, minute=0)
實例化日期時間
類方法
datetime.today()
當前日期時間
datetime.fromtimestamp(t)
秒數 => 日期時間
datetime.strptime(date_string, format)
字符串 => 日期時間
實例方法
DATE.date()
返回日期實例
DATE.time()
返回時間實例
DATE.weekday()
返回0 ~ 6 (Mon ~ Sun)
DATE.timetuple()
返回時間元組
DATE.timestamp()
返回秒數
DATE.replace(year, month, day, hour, minute)
更新日期時間
兩個 datetime 實例(日期時間)相減可以得到 timedelta 實例(時間差)
時間差:
timedelta(days, seconds, minutes, hours, weeks)
實例化時間差
同類可加減比較,可與int乘除
實例屬性
DELTA.days
天數
DELTA.seconds
秒數
有時浮點數運算會損失精度,在涉及除法的時候使用 Fraction 實例(分數)代替有奇效
但同時分數運算的耗時會因為求最大公約數(輾轉相除法)而增加
Fraction 實例支持很多和 int 的運算,慢慢探索
Fraction(numerator, denominator)
返回分數實例
實例屬性
FRACT.numerator
返回分子
FRACT.denominator
返回分母
堆在解決“前 n 大”、“前 n 小”的問題上有很高的效率
這個庫只提供了小根堆的函數(大根堆都是隱藏函數),要使用大根堆的話對所有元素取負就行了
小根堆:
heapify(seq)
原地小根堆化
heappush(heap, item)
添加堆結點
heappop(heap)
彈出堆頂,並重排
nsmallest(n, seq, key)
按key返回升序前n元素
nlargest(n, seq, key)
按key返回降序前n元素
heapreplace(heap, item)
pop -> push
heappushpop(heap, item)
push -> pop
迭代工具庫封裝了一些迭代操作
accumulate(seq, operator)
返回前綴和
chain(*seq)
鏈式連接迭代器
cycle(seq)
返回循環鏈表
無限
repeat(seq, times)
有限
combinations(seq, num)
返回不放回
組合序列
combinations_with_replacement(seq, num)
返回有放回
compress(seq, bool_seq)
返回壓縮過濾序列
dropwhile(filter, seq)
濾除直到條件變False
takewhile(filter, seq)
篩選直到條件變False
數值操作:
pi
п
isnan(x)
判斷nan
isinf(x)
判斷inf
isfinite(x)
是否有限
tau
2п
nan
nan
inf
∞
isclose(a, b)
是否相近
開方的速度:math.isqrt 函數 (取整) > math.sqrt 函數 > 運算符
求冪的速度:
當然,在取模時還是自編的二分快速冪最快
運算函數:
sqrt(x) / isqrt(x)
x ^ 0.5
pow(x, a)
x ^ a
factorial(x)
x!
gcd(a, b)
最大公約數
prod(iter)
累乘
perm(n, k) / comb(n, k)
排列數,組合數,C = P / k!
exp(x)
e ^ x
log(x, base)
loga(x),a默認為e
sin(x) / cos(x) / tan(x)
正三角
asin(x) / acos(x) / atan(x)
反三角
ceil(x) / floor(x)
取整
degrees(x) / radians(x)
弧度 <-> 角度
dist(point_1, point_2)
歐式距離
hypot(*xyz)
向量的模
我覺得這是個必學的庫,用於字符串的匹配
會這個的話考試碰上亂殺,不會的話等著被亂殺
正則表達式:
.
換行符之外的任意字符
\d
數字
\s
空白字符
\w
單詞、數字、下劃線字符
\D
非數字
\S
非空白字符
\W
非單詞、數字、下劃線字符
^
置於開頭,表只匹配前綴,同\A
$
置於結尾,表只匹配後綴,同\Z
|
表示"或"
( )
表達式的內容分組
(?:表非捕獲組
[ ]
其中為
字符類
-:在中間則描述范圍,否則為普通字符
^:在首位表不在其中的任何字符,否則為普通字符
[\u4e00-\u9fa5]
中文
{ }
數字或范圍表前一字符重復次數
{ }?:啟用非貪婪
*
等價於 {0,}
*?:啟用非貪婪
+
等價於 {1,}
+?:啟用非貪婪
?
等價於 {0,1}
??:啟用非貪婪
(.*?)
非貪婪截取內容
匹配函數:
compile(pattern)
返回正則表達式模式實例
search(pattern, string)
返回匹配結果
match(pattern, string)
返回字符串前綴的匹配結果
findall(pattern, string)
返回匹配的字符串列表
sub(pattern, repl, string)
匹配並替換成新字符
匹配實例:
MATCH.group()
匹配內容
MATCH.start()
起始位置
MATCH.end()
結束位置
MATCH.span()
匹配范圍
“基礎練習”裡面雖然都是無腦題,但是還是得刷一下的,主要是了解藍橋杯的測評方法
然後刷題以“歷屆試題”為主,但是這份題不太全面,建議在 CSDN 上找別人的題解跟著練
我自己在准備藍橋杯的時候也寫了不少題解,可以看我的專欄:Link ~
C 語言網的題集收錄了藍橋杯的考試真題,而且比較全面,強力推薦:C語言網:編程題庫

不知道 C 語言網用的 Python 版本是幾,不支持 math 庫的一些函數(如 isqrt)
力扣的題型和藍橋杯真題的題型很不一樣(主刷力扣 = 完蛋),但是力扣有很多的優點:
我寫的題集涉及到了較多的數據結構,這些在藍橋杯測評系統、C語言網是學不到的
有些題目比較簡單,可以選擇性地刷一些:LeetCode:算法面試題匯總
考試是不能帶模板的,所以建議理解構造思路,自己多默寫
標 * 的表示重要性較低
當答案涉及求余的操作時,使用自己寫的二分快速冪會更快,例如求解 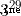 時:
時:
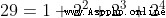

由 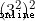 得到
得到 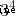 ,由
,由 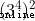 得到
得到 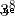 ,以此類推,再累乘就行了
,以此類推,再累乘就行了
def qpow(base, time, mod):
''' 二分快速冪
mod: 求余數'''
result = 1
while time:
if time & 1:
result = result * base % mod
base = base ** 2 % mod
time >>= 1
return result目前我還沒有遇見用並查集的題目,有備無患嘛:
class Disjoint_Set:
''' 並查集'''
def __init__(self, length):
# 記錄前驅結點
self._pre = list(range(length))
# 記錄結點級別
self._rank = [1] * length
def find(self, i):
while self._pre[i] != i:
i = self._pre[i]
return i
def is_same(self, i, j):
return self.find(i) == self.find(j)
def join(self, i, j):
# 訪問結點前驅
i, j = map(self.find, [i, j])
# 前驅不同, 需要合並
if i != j:
# 訪問前驅級別
rank_i, rank_j = self._rank[i], self._rank[j]
# 前驅級別不同: 級別高的作為根結點
if rank_i > rank_j:
self._pre[j] = i
elif rank_i < rank_j:
self._pre[i] = j
# 前驅級別相同: 提高一個前驅的級別, 作為根結點
else:
self._rank[i] += 1
self._pre[j] = i
def __str__(self):
return str(self._pre)
__repr__ = __str__這個歐拉篩和最簡單的那種篩法相比,其實就是生成合數的方式不同:
def prime_filter(n):
''' 質數篩選 (線性復雜度)
return: 質數集合'''
# 質數標記、質數集合
is_prime = [True] * (n + 1)
prime_set = []
# 枚舉 [2, n]
for i in range(2, n + 1):
# 當有質數標記, 添加到質數集合
if is_prime[i]: prime_set.append(i)
# 標記合數
for p in prime_set:
comp = i * p
# 退出: 合數越界
if comp > n: break
# 標記: 合數
is_prime[comp] = False
# 退出: i % p == 0
if i % p == 0: break
return prime_set試除法是最基本的分解方法,在 Python 中 Pollard rho 算法對 7e5 以上的大數分解更快:大數的質因數分解 Python
def try_divide(n, factor={}):
''' 試除法分解'''
i, bound = 2, isqrt(n)
while i <= bound:
if n % i == 0:
# 計數 + 整除
cnt = 1
n //= i
while n % i == 0:
cnt += 1
n //= i
# 記錄冪次, 更新邊界
factor[i] = factor.get(i, 0) + cnt
bound = isqrt(n)
i += 1
if n > 1: factor[n] = 1
return factordef all_factor(n):
''' 所有因數'''
p_factor = try_divide(n)
factor = [1]
for i in p_factor:
temp = []
for p in range(1, p_factor[i] + 1):
temp += [i ** p * j for j in factor]
factor += temp
return factor以 [8, 3, 7, 6, 5, 4, 2, 1] 為例,這個函數完成的工作就是:
def next_permutation(seq):
''' 找到下個字典序
exp: 8 3 7 6 5 4 2 1
| | '''
n = len(seq)
left = -1
for idx in range(n - 2, -1, -1):
# 找到順序區的右邊界
if seq[idx] < seq[idx + 1]:
left = idx
break
if left != -1:
for right in range(n - 1, left, -1):
# 找到交換位
if seq[left] < seq[right]:
seq[left], seq[right] = seq[right], seq[left]
# 逆轉逆序區
seq[left + 1:] = reversed(seq[left + 1:])
return seq
else:
return NoneDijkstra:使用額外的空間記錄“單源最短路”、“未完成標記”,主體使用 while 循環
def Dijkstra(source, adj):
''' 單源最短路徑 (不帶負權)
source: 源點
adj: 圖的鄰接矩陣'''
vex_num = len(adj)
# 記錄單源最短路
distance = [inf] * vex_num
distance[source] = 0
# 記錄是否未完成
undone = [True] * vex_num
while 1:
min_idx, min_val = -1, inf
for idx, (dist, flag) in enumerate(zip(distance, undone)):
# 找到 min_idx, min_dist
if flag and dist < min_val:
min_idx, min_val = idx, dist
if min_idx != -1:
undone[min_idx] = False
for idx, (dist, flag) in enumerate(zip(distance, undone)):
if flag:
state = min_val + adj[min_idx][idx]
distance[idx] = min([state, distance[idx]])
else:
return distanceSPFA:使用額外的空間記錄“單源最短路”、“頂點隊列”、“在隊標記”、“入隊次數”,主體使用 while 循環(隊列非空)
def SPFA(source, adj):
''' 單源最短路徑 (帶負權)
source: 源點
adj: 圖的鄰接矩陣'''
vex_num = len(adj)
# 記錄單源最短路
distance = [inf] * vex_num
distance[source] = 0
# 記錄是否存在隊列中
exist = [False] * vex_num
exist[source] = True
# 記錄進入隊列的次數
count = [0] * vex_num
count[source] = 1
# 初始化隊列
queue = [source]
while queue:
# 隊列: 彈出當前訪問點
visit = queue.pop(0)
cur_dist = distance[visit]
exist[visit] = False
for next_, weight in enumerate(adj[visit]):
dist, flag, cnt = distance[next_], exist[next_], count[next_]
new_dist = cur_dist + weight
# 更新: 出邊dist值
if new_dist < dist:
dist = new_dist
if not flag:
# 入隊: 被更新點
flag = True
cnt += 1
queue.append(next_)
# 終止: 存在負環
if cnt > vex_num: return False
distance[next_], exist[next_], count[next_] = dist, flag, cnt
return distancedef Floyd(adj):
''' 多源最短路徑 (帶負權)
adj: 圖的鄰接矩陣'''
vertex_num = len(adj)
for mid in range(vertex_num):
for source in range(vertex_num):
for end in range(vertex_num):
attempt = adj[source][mid] + adj[mid][end]
adj[source][end] = min([adj[source][end], attempt])def topo_sort(in_degree, adj):
''' AOV網拓撲排序 (最小字典序)
in_degree: 入度表
adj: 圖的鄰接矩陣'''
seq = []
while 1:
visit = -1
for idx, degree in enumerate(in_degree):
if degree == 0:
visit = idx
in_degree[idx] = inf
# 記錄: 入度為0的頂點
seq.append(visit)
for out, weight in enumerate(adj[visit]):
if 0 < weight < inf: in_degree[out] -= 1
break
# 搜索結束 / 存在環: 退出
if visit == -1: break
return seqdef Prim(source, adj):
''' 最小生成樹
source: 源點
adj: 圖的鄰接表'''
low_cost = adj[source].copy()
# 記錄 low_cost 中的邊權對應的起點
last_vex = [source for _ in range(len(adj))]
# 記錄頂點是否已作為出點
undone = [True for _ in range(len(adj))]
undone[source] = False
edges = []
while any(undone):
# 找到權值最小邊的端點
next_ = low_cost.index(min(low_cost))
begin = last_vex[next_]
edges.append((begin, next_))
# 標記出點
low_cost[next_] = inf
undone[next_] = False
for idx, (old, new, flag) in enumerate(zip(low_cost, adj[next_], undone)):
if flag and old > new:
# 滿足更優則更新
low_cost[idx] = new
last_vex[idx] = next_
return edgesdef Euler_path(source, adj, search):
''' 歐拉路徑 (遍歷邊各 1 次)
source: 路徑起點
adj: 圖的鄰接表
search: 出邊搜索函數'''
path = []
stack = [source]
while stack:
# 訪問: 棧頂頂點
visit = stack[-1]
out = adj[visit]
if out:
visit, out = search(visit, out)
# 入棧: 尚未滿足途徑點條件
if out:
stack.append(visit)
# 入列: 滿足途徑點條件
else:
path.append(visit)
# 入列: 滿足途徑點條件
else:
path.append(stack.pop(-1))
path.reverse()
return path線段樹是個常考的數據結構,但是對於 Python 來說意義不大,用 class 寫一個的話效率太低
講一講咯,樹結點和葉結點都用以下這個類存儲,這個類需要編寫的函數如下:
搜集子結點的 value,並使用 key 求值後,
更新 value 並返回給父結點
利用 mid 屬性對 [left, right] 區間進行劃分
匯總左右子樹查找的結果,返回 key 函數求取的 value
class Seg_Tree:
''' 線段樹
key: 樹結點的求值函數'''
def __init__(self, left, right):
self.value = None
self.l, self.r = left, right
self._is_leaf = left == right
# 創建左右子樹
if not self._is_leaf:
self.mid = (left + right) // 2
self._children = [Seg_Tree(left, self.mid),
Seg_Tree(self.mid + 1, right)]
@staticmethod
def key(args):
''' 線段樹求值函數
return: 與葉結點 value 的形式保持一致'''
return max(args)
def check(self, *args):
''' 檢查訪問是否越界'''
left, right = args if len(args) == 2 else args * 2
return self.l <= left and right <= self.r
def update(self):
''' 更新樹結點的值'''
if not self._is_leaf:
args = [child.update() for child in self._children]
self.value = self.key(args)
return self.value
def __setitem__(self, idx, value):
assert self.check(idx)
# 設置葉結點
if self._is_leaf:
self.value = value
else:
# 查找葉結點
for child in self._children:
if child.check(idx):
child[idx] = value
def __getitem__(self, range_):
''' range_: 區間 [l, r]'''
left, right = range_
assert self.check(left, right)
# 區間相等
if left == self.l and right == self.r:
return self.value
else:
args = []
# 在左子樹中搜索
if left <= self.mid:
r_bound = min([right, self.mid])
args.append(self._children[0][left, r_bound])
# 在右子樹中搜索
if self.mid + 1 <= right:
l_bound = max([self.mid + 1, left])
args.append(self._children[1][l_bound, right])
return self.key(args)
def __str__(self):
if self._is_leaf:
return str(self.value)
return str(self._children)
__repr__ = __str__使用的方法如下:
# 初始化空線段樹
tree = Seg_Tree(0, 1023)
# 設置葉結點的值: 調用 __setitem__
for i in range(1024):
tree[i] = i
# 更新樹結點的值
tree.update()
# 訪問線段樹的值: 調用 __getitem__
print(tree[333, 888])