I guess it's a race 48.5 about ( Full marks 150). Guangdong total 78 Save one , I only came in at number 33 (42.3%)
In this article , I'll start with “ Knowledge preparation ”、“ Brush question website ”、“ Function templates ” Three aspects explain how to prepare for the Blue Bridge Cup Python Group game
If you get into the national tournament , I want to count the number of people in the province , You can read my article ： Blue Bridge Cup Statistics of the number of people in the province Python Realization
If you don't change the regular expression, leave a message in the comment area , I'll help you with the statistics ~
The official requirement is IDLE, But this year , It can be used PyCharm Of （ It is still necessary to ask clearly ）
use PyCharm If you don't, you should match it 3.8.6 It's a good environment
I mainly read the front of this online class 40 Set , Because I learned tree in my major course 、 chart , So the focus is on dynamic planning 、 knapsack 、 State compression 、 Line segment tree
【 The Blue Bridge Cup 】 Video tutorial （ Introduction learning + Algorithm tutoring ）
https://www.bilibili.com/video/BV1Lb4y1k7K3?
Greedy algorithm , Comparative metaphysics , Practice oriented ：LeetCode： Greedy algorithm problem set
And number theory 、 Computational geometry 、 The prefix and 、 The difference is the test site , But I don't have a good online class recommendation
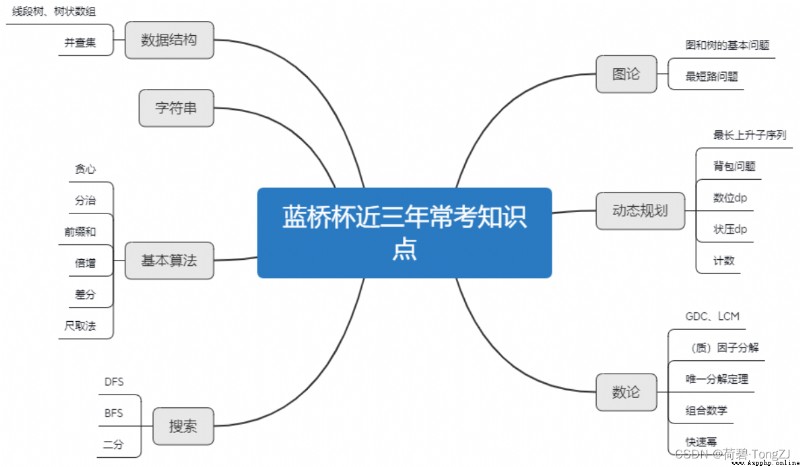
Borrow the thought map of blue bridge cloud class ~
Then when the competition answers , Be sure to look at all the questions first , Because the difficulty of the topic is not necessarily increasing —— You know, I saw the simplest question in the whole volume at the end this year 、 There is no time to do how desperate
Before learning the standard library , First of all, I have to Python Some basic data structures of （ list 、 Tuples 、 Dictionaries 、 character string ……）
And the deeper you know about classes and instances, the better （ As in the case of __call__ A class function of this name ）, This will help you read the source code directly , Raise awareness of the standard library
In general , The performance of standard library functions is the best , So if you can use it, you must use it
about 
,Python 1 It can be done in seconds 8e7 Times operation （ The same is true of addition ）, The time complexity of the code is designed according to the size of the problem
For an ordered sequence , The binary search will be much faster
Ascending
bisect_left(array, x)
Binary search x The location of
insort(array, x)
Dichotomy Insert x
Numerical operations ：
pi
п
isnan(z)
Judge nan
isinf(z)
Judge inf
isfinite(z)
Limited or not
tau
2п
nan
nan
inf
∞
isclose(a, b)
Whether it is similar
cmath Library is a complex number operation library , It is very useful in the Blue Bridge Cup
There are always some problems in the Blue Bridge Cup x-y Find the distance between two points in the coordinate system 、 Angle question , Using the modulo of the complex number 、 Phase angle solution can simplify the code and improve the operation speed
Attribute access ：
z.real
The plural Real component
z.imag
The plural Imaginary part
abs(z)
Plural model
phase(z)
The plural phase angle (-п, п]
z.conjugate()
Corresponding Conjugate complex
rect(r, phi)
Polar coordinates -> The plural
polar(z)
The plural -> Polar coordinates (r, φ)
This library mainly provides counters , It can quickly count the sequence （ Such as a string ） The elements in
Counter ：
Counter(var / **kwargs)
return Counter
CNT.elements()
return Element iterators
CNT.most_common(int)
Returns the specified quantity High frequency value
CNT.update(var)
to update Counter
Add
CNT.subtract(var)
Subtraction
Sometimes the Blue Bridge Cup has some questions about the date , This library matches try - except Statement can determine the validity of a date
time There's no need for Kurt , Not as fast as this library ; Get to know time Floating point seconds of the library 、strptime The method will do
Date time ：
datetime(year, month, day, hour=0, minute=0)
Instantiation date Time
Class method
datetime.today()
At present Date time
datetime.fromtimestamp(t)
Number of seconds => Date time
datetime.strptime(date_string, format)
character string => Date time
Example method
DATE.date()
return Date instance
DATE.time()
return Time example
DATE.weekday()
return 0 ~ 6 (Mon ~ Sun)
DATE.timetuple()
return time tuples
DATE.timestamp()
return Number of seconds
DATE.replace(year, month, day, hour, minute)
to update Date time
Two datetime example （ Date time ） Subtracting can get timedelta example （ Time difference ）
Time difference ：
timedelta(days, seconds, minutes, hours, weeks)
Instantiation Time difference
The same kind can be added or subtracted , But with int Multiplication and division
Instance attributes
DELTA.days
Days
DELTA.seconds
Number of seconds
Sometimes floating point arithmetic will lose precision , Use when it comes to division Fraction example （ fraction ） Substitution has a miraculous effect
But at the same time, the time-consuming of fractional operation will be caused by finding the greatest common divisor （ division ） And increase
Fraction Instances support many and int Arithmetic , Explore slowly
Fraction(numerator, denominator)
return fraction example
Instance attributes
FRACT.numerator
return molecular
FRACT.denominator
return The denominator
Pile up to solve “ front n Big ”、“ front n Small ” Has a high efficiency on the problem of
This library only provides functions of small root heap （ The large root heap is a hidden function ）, If you want to use a large root heap, just negative all the elements
Heap ：
heapify(seq)
In situ Small root heap
heappush(heap, item)
add to Heap nodes
heappop(heap)
eject Top of pile , and rearrangement
nsmallest(n, seq, key)
Press key return Before ascending n Elements
nlargest(n, seq, key)
Press key return Before descending n Elements
heapreplace(heap, item)
pop -> push
heappushpop(heap, item)
push -> pop
The iteration tool library encapsulates some iteration operations
accumulate(seq, operator)
return The prefix and
chain(*seq)
The chain Connect iterators
cycle(seq)
return Circular linked list
Infinite
repeat(seq, times)
Co., LTD.
combinations(seq, num)
return Don't put back
Combining sequences
combinations_with_replacement(seq, num)
return Put it back
compress(seq, bool_seq)
return Compressed filter sequence
dropwhile(filter, seq)
Filter out Until the conditions change False
takewhile(filter, seq)
Screening Until the conditions change False
Numerical operations ：
pi
п
isnan(x)
Judge nan
isinf(x)
Judge inf
isfinite(x)
Limited or not
tau
2п
nan
nan
inf
∞
isclose(a, b)
Whether it is similar
The speed of square root ：math.isqrt function ( integer ) > math.sqrt function > Operator
The speed of exponentiation ：
Of course , When taking the module, it is still the fastest binary fast power compiled by ourselves
Operation function ：
sqrt(x) / isqrt(x)
x ^ 0.5
pow(x, a)
x ^ a
factorial(x)
x!
gcd(a, b)
greatest common divisor
prod(iter)
Multiplicative multiplication
perm(n, k) / comb(n, k)
array Count , Combine Count ,C = P / k!
exp(x)
e ^ x
log(x, base)
loga(x),a The default is e
sin(x) / cos(x) / tan(x)
Trigonometry
asin(x) / acos(x) / atan(x)
Anti triangle
ceil(x) / floor(x)
integer
degrees(x) / radians(x)
radian <-> angle
dist(point_1, point_2)
European style distance
hypot(*xyz)
Vectorial model
I think this is a must learn library , For string matching
If you can do this, you will encounter murder in the exam , If not, you will be killed
Regular expressions ：
.
Beyond the newline Any character
\d
Numbers
\s
blank character
\w
word 、 Numbers 、 Underline character
\D
The digital
\S
Not Blank word operator
\W
Not word 、 Numbers 、 Underscore character
^
in start , The table only matches Prefix , Same as \A
$
in ending , The table only matches suffix , Same as \Z
|
Express " or "
( )
The content of the expression grouping
(?： surface Non capturing group
[ ]
Among them is
Character class
-： stay middle Describe Range , otherwise by Ordinary character
^： stay First place surface Not in it Any character of , otherwise by Ordinary character
[\u4e00-\u9fa5]
chinese
{ }
Numbers or Range The previous character of the table Repeat the number
{ }?： Enable Not greed
*
Equivalent to {0,}
*?： Enable Not greed
+
Equivalent to {1,}
+?： Enable Not greed
?
Equivalent to {0,1}
??： Enable Not greed
(.*?)
Not greed Intercept content
Match function ：
compile(pattern)
Returns the regular expression Pattern example
search(pattern, string)
return Matching results
match(pattern, string)
return character strand Prefix Of Matching results
findall(pattern, string)
return matching Of String list
sub(pattern, repl, string)
Match and Replace Into new characters
Match instance ：
MATCH.group()
matching Content
MATCH.start()
start Location
MATCH.end()
end Location
MATCH.span()
matching Range
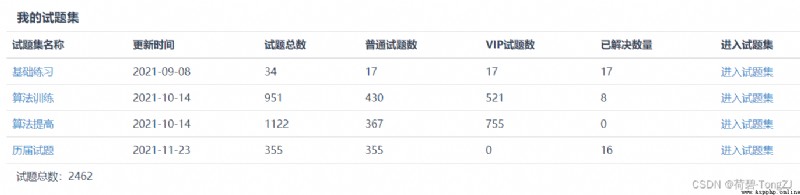
“ Based on practice ” Although there are no brain problems , But I still have to brush it , Mainly to understand the evaluation method of the Blue Bridge Cup
Then brush the questions with “ Past questions ” Mainly , But this question is not comprehensive , It is suggested that CSDN Find someone else's solution and practice
I also wrote a lot of questions when preparing for the Blue Bridge Cup , You can read my column ：Link ~
C The collection of questions on langyu.com contains the real test questions of the Blue Bridge Cup , And it's more comprehensive , Strongly recommend ：C Language network ： Programming question bank
I do not know! C Language network used Python What's the version , I won't support it math Some functions of the library （ Such as isqrt）
The question type of Li Kou is very different from that of the real blue bridge cup （ Main brush force buckle = Be finished ）, But the buckle has many advantages ：
The question set I wrote involves a lot of data structures , These are in the Blue Bridge Cup evaluation system 、C You can't learn language net
Some topics are simple , You can selectively brush some ：LeetCode： Algorithm interview question summary
You can't take a template for an exam , Therefore, it is suggested to understand the construction idea , Write more by yourself
mark * Is less important
When the answer involves the operation of remainder , It's faster to use your own bisection power , For example, solve 
when ：
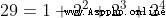
from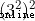 
obtain 
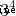, from 
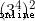obtain 
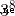, And so on , If you are tired, you will be fine
def qpow(base, time, mod):
''' A fast power of two
mod: Mod '''
result = 1
while time:
if time & 1:
result = result * base % mod
base = base ** 2 % mod
time >>= 1
return resultAt present, I haven't met the problem of using and searching sets , Be prepared for nothing ：
class Disjoint_Set:
''' Union checking set '''
def __init__(self, length):
# Record the precursor node
self._pre = list(range(length))
# Record node level
self._rank = [1] * length
def find(self, i):
while self._pre[i] != i:
i = self._pre[i]
return i
def is_same(self, i, j):
return self.find(i) == self.find(j)
def join(self, i, j):
# Access node precursor
i, j = map(self.find, [i, j])
# The precursors are different , Need merger
if i != j:
# Access the precursor level
rank_i, rank_j = self._rank[i], self._rank[j]
# Different levels of precursors : High level nodes are used as root nodes
if rank_i > rank_j:
self._pre[j] = i
elif rank_i < rank_j:
self._pre[i] = j
# The precursor level is the same : Raise the level of a precursor , As the root node
else:
self._rank[i] += 1
self._pre[j] = i
def __str__(self):
return str(self._pre)
__repr__ = __str__This Euler sieve is compared with the simplest sieve method , In fact, there are different ways to generate composite numbers ：
def prime_filter(n):
''' Prime screening ( Linear complexity )
return: Prime set '''
# Prime number mark 、 Prime set
is_prime = [True] * (n + 1)
prime_set = []
# enumeration [2, n]
for i in range(2, n + 1):
# When marked with prime numbers , Add to prime set
if is_prime[i]: prime_set.append(i)
# Marked composite number
for p in prime_set:
comp = i * p
# sign out : Composite number is out of bounds
if comp > n: break
# Mark : Sum
is_prime[comp] = False
# sign out : i % p == 0
if i % p == 0: break
return prime_setTrial division is the most basic method of decomposition , stay Python in Pollard rho Algorithm to 7e5 The decomposition of the above large numbers is faster ： Prime factorization of large numbers Python
def try_divide(n, factor={}):
''' Try to divide '''
i, bound = 2, isqrt(n)
while i <= bound:
if n % i == 0:
# Count + to be divisible by
cnt = 1
n //= i
while n % i == 0:
cnt += 1
n //= i
# Record power , Update boundaries
factor[i] = factor.get(i, 0) + cnt
bound = isqrt(n)
i += 1
if n > 1: factor[n] = 1
return factordef all_factor(n):
''' All factors '''
p_factor = try_divide(n)
factor = [1]
for i in p_factor:
temp = []
for p in range(1, p_factor[i] + 1):
temp += [i ** p * j for j in factor]
factor += temp
return factorWith [8, 3, 7, 6, 5, 4, 2, 1] For example , What this function does is ：
def next_permutation(seq):
''' Find the next dictionary order
exp: 8 3 7 6 5 4 2 1
| | '''
n = len(seq)
left = -1
for idx in range(n - 2, -1, -1):
# Find the right boundary of the sequence area
if seq[idx] < seq[idx + 1]:
left = idx
break
if left != -1:
for right in range(n - 1, left, -1):
# Find the swap bit
if seq[left] < seq[right]:
seq[left], seq[right] = seq[right], seq[left]
# Reverse order
seq[left + 1:] = reversed(seq[left + 1:])
return seq
else:
return NoneDijkstra： Use extra space to record “ Single source shortest path ”、“ Incomplete marking ”, Subject use while loop
def Dijkstra(source, adj):
''' Single source shortest path ( Without negative weight )
source: Source point
adj: The adjacency matrix of a graph '''
vex_num = len(adj)
# Record the shortest circuit of single source
distance = [inf] * vex_num
distance[source] = 0
# Whether the record is incomplete
undone = [True] * vex_num
while 1:
min_idx, min_val = -1, inf
for idx, (dist, flag) in enumerate(zip(distance, undone)):
# find min_idx, min_dist
if flag and dist < min_val:
min_idx, min_val = idx, dist
if min_idx != -1:
undone[min_idx] = False
for idx, (dist, flag) in enumerate(zip(distance, undone)):
if flag:
state = min_val + adj[min_idx][idx]
distance[idx] = min([state, distance[idx]])
else:
return distanceSPFA： Use extra space to record “ Single source shortest path ”、“ Vertex queue ”、“ In line marking ”、“ The number of times to join the team ”, Subject use while loop （ The queue is not empty ）
def SPFA(source, adj):
''' Single source shortest path ( With negative weight )
source: Source point
adj: The adjacency matrix of a graph '''
vex_num = len(adj)
# Record the shortest circuit of single source
distance = [inf] * vex_num
distance[source] = 0
# Whether the record exists in the queue
exist = [False] * vex_num
exist[source] = True
# Record the number of times you entered the queue
count = [0] * vex_num
count[source] = 1
# Initialize queue
queue = [source]
while queue:
# queue : Pop up the current access point
visit = queue.pop(0)
cur_dist = distance[visit]
exist[visit] = False
for next_, weight in enumerate(adj[visit]):
dist, flag, cnt = distance[next_], exist[next_], count[next_]
new_dist = cur_dist + weight
# to update : Out of the way dist value
if new_dist < dist:
dist = new_dist
if not flag:
# The team : Updated point
flag = True
cnt += 1
queue.append(next_)
# End : There are negative rings
if cnt > vex_num: return False
distance[next_], exist[next_], count[next_] = dist, flag, cnt
return distancedef Floyd(adj):
''' Multi source shortest path ( With negative weight )
adj: The adjacency matrix of a graph '''
vertex_num = len(adj)
for mid in range(vertex_num):
for source in range(vertex_num):
for end in range(vertex_num):
attempt = adj[source][mid] + adj[mid][end]
adj[source][end] = min([adj[source][end], attempt])def topo_sort(in_degree, adj):
''' AOV Network topology sorting ( Minimum dictionary order )
in_degree: On the scale
adj: The adjacency matrix of a graph '''
seq = []
while 1:
visit = -1
for idx, degree in enumerate(in_degree):
if degree == 0:
visit = idx
in_degree[idx] = inf
# Record : The degree of 0 The summit of
seq.append(visit)
for out, weight in enumerate(adj[visit]):
if 0 < weight < inf: in_degree[out] -= 1
break
# End of the search / Existential ring : sign out
if visit == -1: break
return seqdef Prim(source, adj):
''' Minimum spanning tree
source: Source point
adj: Adjacency table of graph '''
low_cost = adj[source].copy()
# Record low_cost The starting point corresponding to the edge weight in
last_vex = [source for _ in range(len(adj))]
# Record whether the vertex has been used as the exit point
undone = [True for _ in range(len(adj))]
undone[source] = False
edges = []
while any(undone):
# Find the endpoint of the edge with the lowest weight
next_ = low_cost.index(min(low_cost))
begin = last_vex[next_]
edges.append((begin, next_))
# Mark the point
low_cost[next_] = inf
undone[next_] = False
for idx, (old, new, flag) in enumerate(zip(low_cost, adj[next_], undone)):
if flag and old > new:
# Meet better, then update
low_cost[idx] = new
last_vex[idx] = next_
return edgesdef Euler_path(source, adj, search):
''' Euler path ( Traverse each side 1 Time )
source: Path start
adj: Adjacency table of graph
search: Edge search function '''
path = []
stack = [source]
while stack:
# visit : Top of stack
visit = stack[-1]
out = adj[visit]
if out:
visit, out = search(visit, out)
# Push : The waypoint conditions have not been met
if out:
stack.append(visit)
# List : Meet the conditions of the approach point
else:
path.append(visit)
# List : Meet the conditions of the approach point
else:
path.append(stack.pop(-1))
path.reverse()
return pathThe line segment tree is a common data structure , But for Python It doesn't make much sense , use class It is too inefficient to write one
Tell me about it , Both tree nodes and leaf nodes are stored in the following class , The functions that this class needs to write are as follows ：
Search the set of child nodes value, And use key After evaluation ,
to update value And return to the parent node
utilize mid Property right [left, right] Divide the interval
Summarize the search results of the left and right subtrees , return key Function value
class Seg_Tree:
''' Line segment tree
key: Evaluation function of tree node '''
def __init__(self, left, right):
self.value = None
self.l, self.r = left, right
self._is_leaf = left == right
# Create left and right subtrees
if not self._is_leaf:
self.mid = (left + right) // 2
self._children = [Seg_Tree(left, self.mid),
Seg_Tree(self.mid + 1, right)]
@staticmethod
def key(args):
''' Segment tree evaluation function
return: And leaf nodes value In the same form '''
return max(args)
def check(self, *args):
''' Check whether the access is out of bounds '''
left, right = args if len(args) == 2 else args * 2
return self.l <= left and right <= self.r
def update(self):
''' Update the values of tree nodes '''
if not self._is_leaf:
args = [child.update() for child in self._children]
self.value = self.key(args)
return self.value
def __setitem__(self, idx, value):
assert self.check(idx)
# Set leaf nodes
if self._is_leaf:
self.value = value
else:
# Find leaf nodes
for child in self._children:
if child.check(idx):
child[idx] = value
def __getitem__(self, range_):
''' range_: Section [l, r]'''
left, right = range_
assert self.check(left, right)
# Interval equality
if left == self.l and right == self.r:
return self.value
else:
args = []
# Search in the left subtree
if left <= self.mid:
r_bound = min([right, self.mid])
args.append(self._children[0][left, r_bound])
# Search in the right subtree
if self.mid + 1 <= right:
l_bound = max([self.mid + 1, left])
args.append(self._children[1][l_bound, right])
return self.key(args)
def __str__(self):
if self._is_leaf:
return str(self.value)
return str(self._children)
__repr__ = __str__The methods used are as follows ：
# Initialize the empty segment tree
tree = Seg_Tree(0, 1023)
# Set the value of leaf node : call __setitem__
for i in range(1024):
tree[i] = i
# Update the values of tree nodes
tree.update()
# Accessing the values of the segment tree : call __getitem__
print(tree[333, 888])
The front end (HTML) can receive the list data of the back end (Python view.py) render. How can the front end display a value of the list in a grid through a table?
The phenomenon and background
