leetcode 2304. Minimum Path Cost in a Grid（python）

Keep creating , Accelerate growth ！ This is my participation 「 Nuggets day new plan · 6 Yuegengwen challenge 」 Of the 27 God , Click to see the event details

describe

You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1). Note that it is not possible to move from cells in the last row.

Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.

The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.

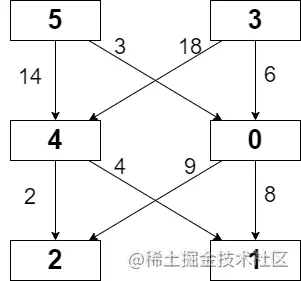
Example 1:

Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
Output: 17
Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.
 Copy code 

Example 2:

Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
Output: 6
Explanation: The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.
 Copy code 

Note:

m == grid.length
n == grid[i].length
2 <= m, n <= 50
grid consists of distinct integers from 0 to m * n - 1.
moveCost.length == m * n
moveCost[i].length == n
1 <= moveCost[i][j] <= 100
 Copy code 

analysis

According to the meaning , Given a 0 Indexed m x n Integer matrix grid , from 0 To m * n - 1 Is composed of different integers . You can move from one cell in this matrix to any other cell in the next row . It should be noted that , Stop moving cells to the last row . Every possible move has a size of (m * n) x n Of 0 Indexes 2D Array moveCost Price given , among moveCost[i][j] Yes, the slave value is i The cell of moves to the j The cost of the cells in the column . The cost of a path in a grid is the sum of all cell values accessed plus the cost of all moves . Returns the minimum cost of the path from any cell in the first row to the end of any cell in the last row .

answer

class Solution(object):
def minPathCost(self, grid, moveCost):
"""
:type grid: List[List[int]]
:type moveCost: List[List[int]]
:rtype: int
"""
M = len(grid)
N = len(grid[0])
dp = [[float('inf')] * N for _ in range(M)]
dp[0] = grid[0]
for i in range(1, M):
for j in range(N):
for k in range(N):
dp[i][j] = min(dp[i][j], grid[i][j] + dp[i-1][k] + moveCost[grid[i-1][k]][j])
return min(dp[-1])
 Copy code 

Running results

34 / 34 test cases passed.
Status: Accepted
Runtime: 2733 ms
Memory Usage: 18.2 MB
 Copy code 

Original link

leetcode.com/contest/wee…

Your support is my greatest motivation