信貸風控是數據挖掘算法最成功的應用之一，這在於金融信貸行業的數據量很充足，需求場景清晰及豐富。
信貸風控簡單來說就是判斷一個人借了錢後面（如下個月的還款日）會不會按期還錢。更專業來說，信貸風控是還款能力及還款意願的綜合考量，根據這預先的判斷為信任依據進行放貸，以此大大提高了金融業務效率。
與其他機器學習的工業場景不同，金融是極其厭惡風險的領域，其特殊性在於非常側重模型的解釋性及穩定性。業界通常的做法是基於挖掘多維度的特征建立一套可解釋及效果穩定的規則及風控模型對每筆訂單/用戶/行為做出判斷決策。
其中，對於（貸前）申請前的風控模型，也稱為申請評分卡--A卡。A卡是風控的關鍵模型，業界共識是申請評分卡可以覆蓋80%的信用風險。此外還有貸中行為評分卡B卡、催收評分卡C卡，以及反欺詐模型等等。
A卡（Application score card）。目的在於預測申請時（申請信用卡、申請貸款）對申請人進行量化評估。B卡（Behavior score card）。目的在於預測使用時點（獲得貸款、信用卡的使用期間）未來一定時間內逾期的概率。C卡（Collection score card）。目的在於預測已經逾期並進入催收階段後未來一定時間內還款的概率。
一個好的特征，對於模型和規則都是至關重要的。像申請評分卡--A卡，主要可以歸到以下3方面特征：
1、信貸歷史類：信貸交易次數及額度、收入負債比、查詢征信次數、信貸歷史長度、新開信貸賬戶數、額度使用率、逾期次數及額度、信貸產品類型、被追償信息。（信貸交易類的特征重要程度往往是最高的，少了這部分歷史還款能力及意願的信息，風控模型通常直接就廢了。）
2、基本資料及交易記錄類：年齡、婚姻狀況、學歷、工作類型及年薪、工資收入、存款AUM、資產情況、公積金及繳稅、非信貸交易流水等記錄（這類主要是從還款能力上面綜合考量的。還可以結合多方核驗資料的真偽以及共用像手機號、身份證號等團伙欺詐信息，用來鑒別欺詐風險。需要注意的，像性別、膚色、地域、種族、宗教信仰等類型特征使用要謹慎，可能模型會有效果，但也會導致算法歧視問題。）
3、公共負面記錄類：如破產負債、民事判決、行政處罰、法院強制執行、涉賭涉詐黑名單等（這類特征不一定能拿得到數據，且通常缺失度比較高，對模型貢獻一般，更多的是從還款意願/欺詐維度的考慮）
實戰部分我們以經典的申請評分卡為例，使用的中原銀行個人貸款違約預測比賽的數據集，使用信用評分python庫--toad、樹模型Lightgbm及邏輯回歸LR做申請評分模型。（注：文中所涉及的一些金融術語，由於篇幅就不展開解釋了，疑問之處 可以谷歌了解下哈。）
申請評分模型定義主要是通過一系列的數據分析確定建模的樣本及標簽。
首先，補幾個金融風控的術語的說明。概念模糊的話，可以回查再理解下：
逾期期數(M) ：指實際還款日與應還款日之間的逾期天數，並按區間劃分後的逾期狀態。M取自Month on Book的第一個單詞。（注：不同機構所定義的區間劃分可能存在差異） M0：當前未逾期（或用C表示，取自Current） M1：逾期1-30日 M2：逾期31-60日 M3：逾期61-90日 M4：逾期91-120日 M5：逾期121-150日 M6：逾期151-180日 M7+：逾期180日以上
觀察點：樣本層面的時間窗口。 用於構建樣本集的時間點（如2010年10月申請貸款的用戶），不同環節定義不同，比較抽象，這裡舉例說明：如果是申請模型，觀察點定義為用戶申貸時間，取19年1-12月所有的申貸訂單作為構建樣本集；如果是貸中行為模型，觀察點定義為某個具體日期，如取19年6月15日在貸、沒有發生逾期的申貸訂單構建樣本集。
觀察期：特征層面的時間窗口。構造特征的相對時間窗口，例如用戶申請貸款訂前12個月內（2009年10月截至到2010年10月申請貸款前的數據都可以用， 可以有用戶平均消費金額、次數、貸款次數等數據特征）。設定觀察期是為了每個樣本的特征對齊，長度一般根據數據決定。一個需要注意的點是，只能用此次申請前的特征數據，不然就會數據洩露（時間穿越，用未來預測過去的現象）。
表現期：標簽層面的時間窗口。定義好壞標簽Y的時間窗口，信貸風險具有天然的滯後性，因為用戶借款後一個月（第一期）才開始還錢，有得可能還了好幾期才發生逾期。
對於現成的比賽數據，數據特征的時間跨度（觀察期）、數據樣本、標簽定義都是已經提前分析確定下來的。但對於實際的業務來說，數據樣本及模型定義其實也是申請評分卡的關鍵之處。畢竟實際場景裡面可能沒有人扔給你現成的數據及標簽（好壞定義，有些公司的業務會提前分析好給建模人員），然後只是跑個分類模型那麼簡單。
確定建模的樣本量及標簽，也就是模型從多少的數據樣本中學習如何分辨其中的好、壞標簽樣本。如果樣本量稀少、標簽定義有問題，那學習的結果可想而知也會是差的。
對於建模樣本量的確定，經驗上肯定是滿足建模條件的樣本越多越好，一個類別最好有幾千以上的樣本數。但對於標簽的定義，可能我們直觀感覺是比較簡單，比如“好用戶就是沒有逾期的用戶， 壞用戶就是在逾期的用戶”，但具體做量化起來會發現並不簡單，有兩個方面的主要因素需要考量：
【壞的定義】逾期多少天算是壞客戶。比如：只逾期2天算是建模的壞客戶？
根據巴塞爾協議的指導，一般逾期超過90天（M4+）的客戶，即定義為壞客戶。更為通用的，可以使用“滾動率”分析方法（Roll Rate Analysis）確定多少天算是“壞”，基本方法是統計分析出逾期M期的客戶多大概率會逾期M+1期（同樣的，我們不太可能等著所有客戶都逾期一年才最終確定他就是壞客戶。一來時間成本太高，二來這數據樣本會少的可憐）。如下示例，我們通過滾動率分析各期逾期的變壞概率。當前未逾期（M0）下個月保持未逾期的概率99.71%；當前逾期M1，下個月繼續逾期概率為54.34%；當前M2下個月繼續逾期概率就高達*90.04%*。我們可以看出M2是個比較明顯的變壞拐點，可以以M2+作為壞樣本的定義。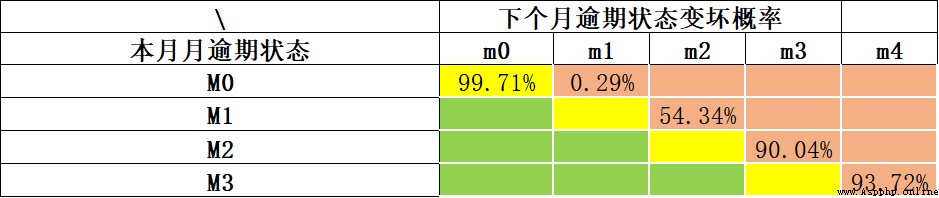
【表現期】借貸申請的時間點（即：觀察點）之後要在多久的時間暴露表現下，才能比較徹底的確定客戶是否逾期。比如：借貸後觀察了一個客戶借貸後60天的那幾個分期的表現都是按時還款，就可以判斷他是好/壞客戶？
這也就是確定表現期，常用的分析方法是Vintage分析（Vintage在信貸領域不僅可以用它來評估客戶好壞充分暴露所需的時間，即成熟期，還可以用它分析不同時期風控策略的差異等），通過分析歷史累計壞用戶暴露增加的趨勢，來確定至少要多少期可以比較全面的暴露出大部分的壞客戶。如下示例的壞定義是M4+，我們可以看出各期的M4+壞客戶經過9或者10個月左右的表現，基本上可以都暴露出來，後面壞客戶的總量就比較平穩了。這裡我們就可以將表現期定位9或者10個月~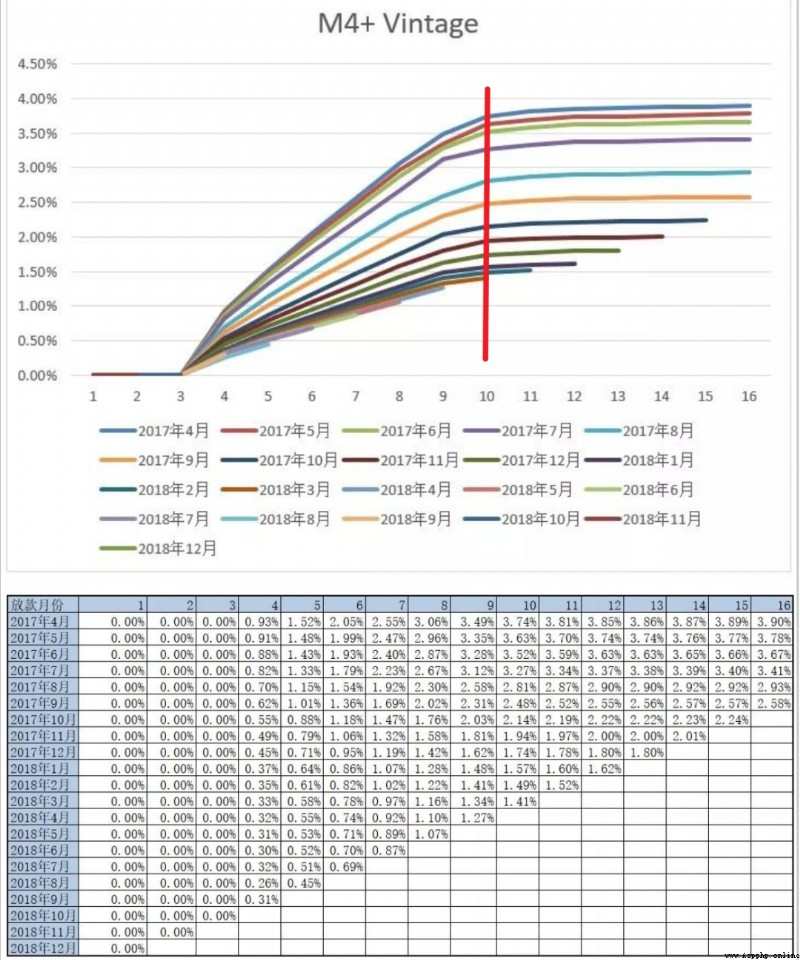
確定了壞的定義以及需要的表現期，我們就可以確定樣本的標簽，最終劃定的建模樣本：
好用戶：表現期（如9個月）內無逾期的用戶樣本。
壞用戶：表現期（如9個月）內逾期（如M2+）的用戶樣本。
灰用戶：表現期內有過逾期行為，但不到壞定義（如M2+）的樣本。注：實踐中經常會把只逾期3天內的用戶也歸為好用戶。
比如現在的時間是2022-10月底，表現期9個月的話，就可以取2022-01月份及之前申請的樣本（這也稱為 觀察點），打上好壞標簽，建模。
通過上面信用評分的介紹，很明顯的好用戶通常遠大於壞用戶的，這是一個類別極不均衡的典型場景，不均衡處理方法下文會談到。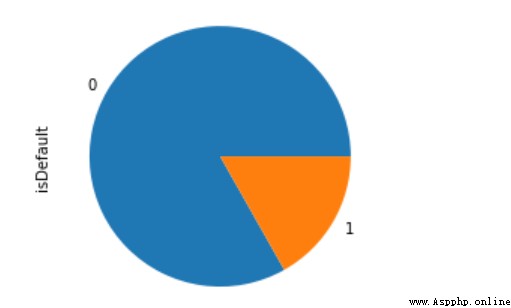
本數據集的數據字典文檔、比賽介紹及本文代碼，可以到https://github.com/aialgorithm/Blog項目相應的代碼目錄下載
該數據集為中原銀行的個人貸款違約預測數據集，個別字段有做了脫敏（金融的數據大都涉及機密）。主要的特征字段有個人基本信息、經濟能力、貸款歷史信息等等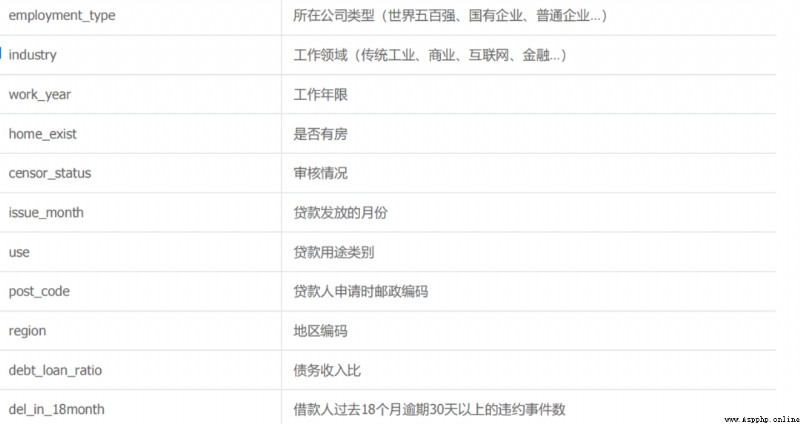
數據有10000條樣本，38維原始特征，其中isDefault為標簽，是否逾期違約。
import pandas as pd
pd.set_option("display.max_columns",50)
train_bank = pd.read_csv('./train_public.csv')
print(train_bank.shape)
train_bank.head()數據預處理主要是對日期信息、噪音數據做下處理，並劃分下類別、數值類型的特征。
# 日期類型：issueDate 轉換為pandas中的日期類型，加工出數值特征
train_bank['issue_date'] = pd.to_datetime(train_bank['issue_date'])
# 提取多尺度特征
train_bank['issue_date_y'] = train_bank['issue_date'].dt.year
train_bank['issue_date_m'] = train_bank['issue_date'].dt.month
# 提取時間diff # 轉換為天為單位
base_time = datetime.datetime.strptime('2000-01-01', '%Y-%m-%d') # 隨機設置初始的基准時間
train_bank['issue_date_diff'] = train_bank['issue_date'].apply(lambda x: x-base_time).dt.days
# 可以發現earlies_credit_mon應該是年份-月的格式，這裡簡單提取年份
train_bank['earlies_credit_mon'] = train_bank['earlies_credit_mon'].map(lambda x:int(sorted(x.split('-'))[0]))
train_bank.head()
# 工作年限處理
train_bank['work_year'].fillna('10+ years', inplace=True)
work_year_map = {'10+ years': 10, '2 years': 2, '< 1 year': 0, '3 years': 3, '1 year': 1,
'5 years': 5, '4 years': 4, '6 years': 6, '8 years': 8, '7 years': 7, '9 years': 9}
train_bank['work_year'] = train_bank['work_year'].map(work_year_map)
train_bank['class'] = train_bank['class'].map({'A': 0, 'B': 1, 'C': 2, 'D': 3, 'E': 4, 'F': 5, 'G': 6})
# 缺失值處理
train_bank = train_bank.fillna('9999')
# 區分 數值 或類別特征
drop_list = ['isDefault','earlies_credit_mon','loan_id','user_id','issue_date']
num_feas = []
cate_feas = []
for col in train_bank.columns:
if col not in drop_list:
try:
train_bank[col] = pd.to_numeric(train_bank[col]) # 轉為數值
num_feas.append(col)
except:
train_bank[col] = train_bank[col].astype('category')
cate_feas.append(col)
print(cate_feas)
print(num_feas)如果是用Lightgbm建模做違約預測，簡單的數據處理，基本上代碼就結束了。lgb樹模型是集成學習的強模型，自帶缺失、類別變量的處理，特征上面不用做很多處理，建模非常方便，模型效果通常不錯，還可以輸出特征的重要性。
（By the way，申請評分卡業界用邏輯回歸LR會比較多，因為模型簡單，解釋性也比較好）。
def model_metrics(model, x, y):
""" 評估 """
yhat = model.predict(x)
yprob = model.predict_proba(x)[:,1]
fpr,tpr,_ = roc_curve(y, yprob,pos_label=1)
metrics = {'AUC':auc(fpr, tpr),'KS':max(tpr-fpr),
'f1':f1_score(y,yhat),'P':precision_score(y,yhat),'R':recall_score(y,yhat)}
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, 'k--', label='ROC (area = {0:.2f})'.format(roc_auc), lw=2)
plt.xlim([-0.05, 1.05]) # 設置x、y軸的上下限，以免和邊緣重合，更好的觀察圖像的整體
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate') # 可以使用中文，但需要導入一些庫即字體
plt.title('ROC Curve')
plt.legend(loc="lower right")
return metrics
# 劃分數據集：訓練集和測試集
train_x, test_x, train_y, test_y = train_test_split(train_bank[num_feas + cate_feas], train_bank.isDefault,test_size=0.3, random_state=0)
# 訓練模型
lgb=lightgbm.LGBMClassifier(n_estimators=5,leaves=5, class_weight= 'balanced',metric = 'AUC')
lgb.fit(train_x, train_y)
print('train ',model_metrics(lgb,train_x, train_y))
print('test ',model_metrics(lgb,test_x,test_y))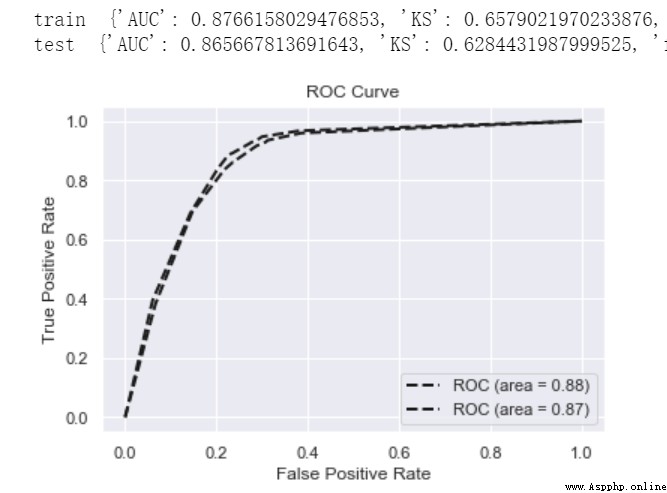
from lightgbm import plot_importance
plot_importance(lgb)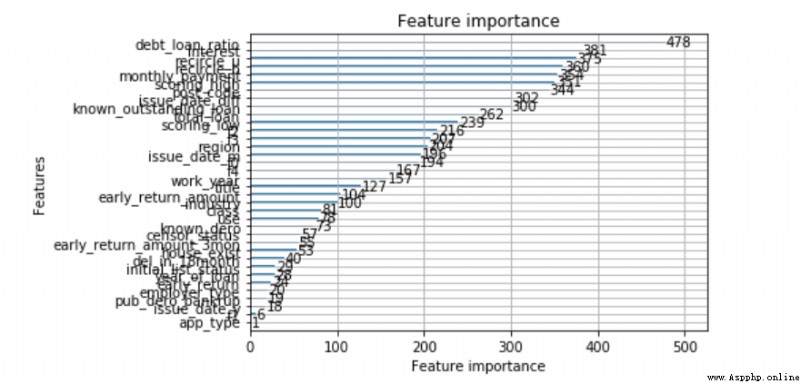
LR即邏輯回歸，是一種廣義線性模型，因為其模型簡單、解釋性良好，在金融行業是最常用的。
也正因為LR過於簡單，沒有非線性能力，所以我們往往需要通過比較復雜的特征工程，如分箱WOE編碼的方法，提高模型的非線性能力。關於LR的原理及優化方法，強烈推薦閱讀下：
《全面解析並實現邏輯回歸(Python)》
《邏輯回歸優化技巧總結（全）》
下面我們通過toad實現特征分析、特征選擇、特征分箱及WOE編碼
# 數據EDA分析
toad.detector.detect(train_bank)
# 特征選擇,根據相關性 缺失率、IV 等指標
train_selected, dropped = toad.selection.select(train_bank,target = 'isDefault', empty = 0.5, iv = 0.05, corr = 0.7, return_drop=True, exclude=['earlies_credit_mon','loan_id','user_id','issue_date'])
print(dropped)
print(train_selected.shape)
# 劃分訓練集 測試集
train_x, test_x, train_y, test_y = train_test_split(train_selected.drop(['loan_id','user_id','isDefault','issue_date','earlies_credit_mon'],axis=1), train_selected.isDefault,test_size=0.3, random_state=0)# 特征的卡方分箱
combiner = toad.transform.Combiner()
# 訓練數據並指定分箱方法
combiner.fit(pd.concat([train_x,train_y], axis=1), y='isDefault',method= 'chi',min_samples = 0.05,exclude=[])
# 以字典形式保存分箱結果
bins = combiner.export()
bins通過特征分箱，每一個特征被離散化為各個分箱。
接下來就是LR特征工程的特色處理了--手動調整分箱的單調性。
這一步的意義更多在於特征的業務解釋性的約束，對於模型的擬合效果影響不一定是正面的。這裡我們主觀認為大多數特征的不同分箱的壞賬率badrate應該是滿足某種單調關系的，而起起伏伏是不太好理解的。如征信查詢次數這個特征，應該是分箱數值越高，壞賬率越大。（注：如年齡特征可能就不滿足這種單調關系）
我們可以查看下ebt_loan_ratio這個變量的分箱情況，根據bad_rate趨勢圖，並保證單個分箱的樣本占比不低於0.05，去調整分箱，達到單調性。（其他的特征可以按照這個方法繼續調整，單調性調整還是挺耗時的）
adj_var = 'scoring_low'
#調整前原來的分箱 [560.4545455, 621.8181818, 660.0, 690.9090909, 730.0, 775.0]
adj_bin = {adj_var: [ 660.0, 700.9090909, 730.0, 775.0]}
c2 = toad.transform.Combiner()
c2.set_rules(adj_bin)
data_ = pd.concat([train_x,train_y], axis=1)
data_['type'] = 'train'
temp_data = c2.transform(data_[[adj_var,'isDefault','type']], labels=True)
from toad.plot import badrate_plot, proportion_plot
# badrate_plot(temp_data, target = 'isDefault', x = 'type', by = adj_var)
# proportion_plot(temp_data[adj_var])
from toad.plot import bin_plot,badrate_plot
bin_plot(temp_data, target = 'isDefault',x=adj_var)調整前
調整後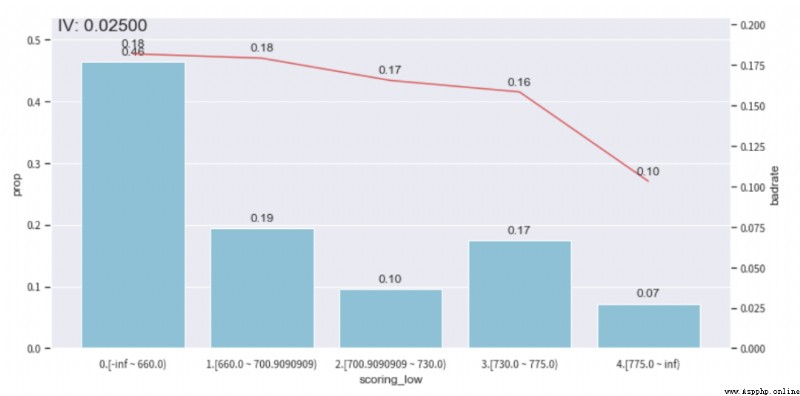
# 更新調整後的分箱
combiner.set_rules(adj_bin)
combiner.export()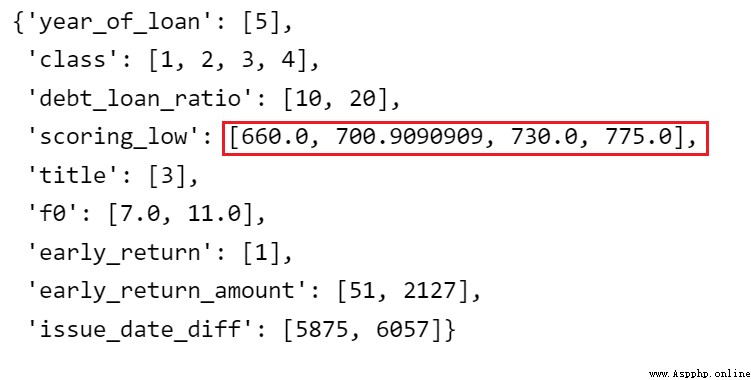
接下來就是對各個特征的分箱做WOE編碼，通過WOE編碼給各個分箱不同的權重，提升LR模型的非線性。
#計算WOE，僅在訓練集計算WOE，不然會標簽洩露
transer = toad.transform.WOETransformer()
binned_data = combiner.transform(pd.concat([train_x,train_y], axis=1))
#對WOE的值進行轉化，映射到原數據集上。對訓練集用fit_transform,測試集用transform.
data_tr_woe = transer.fit_transform(binned_data, binned_data['isDefault'], exclude=['isDefault'])
data_tr_woe.head()
## test woe
# 先分箱
binned_data = combiner.transform(test_x)
#對WOE的值進行轉化，映射到原數據集上。測試集用transform.
data_test_woe = transer.transform(binned_data)
data_test_woe.head()使用woe編碼後的train數據訓練模型。對於金融風控這種極不平衡的數據集，比較常用的做法是做下極少類的正采樣或者使用代價敏感學習class_weight='balanced'，以增加極少類的學習權重。可見：《一文解決樣本不均衡（全）》
對於LR等弱模型，通常會發現訓練集與測試集的指標差異（gap）是比較少的，即很少過擬合現象。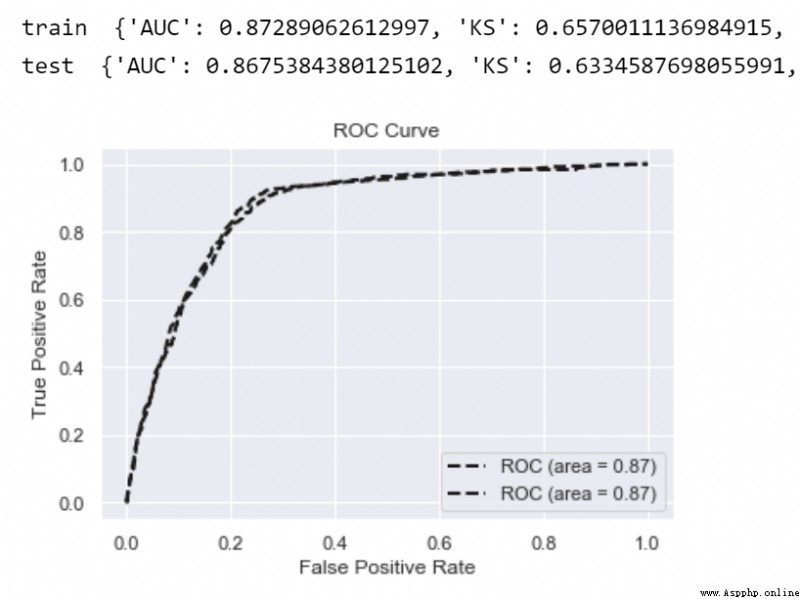
# 訓練LR模型
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(class_weight='balanced')
lr.fit(data_tr_woe.drop(['isDefault'],axis=1), data_tr_woe['isDefault'])
print('train ',model_metrics(lr,data_tr_woe.drop(['isDefault'],axis=1), data_tr_woe['isDefault']))
print('test ',model_metrics(lr,data_test_woe,test_y))利用訓練好的LR模型，輸出（概率）分數分布表，結合誤殺率、召回率以及業務需要可以確定一個合適分數阈值cutoff （注：在實際場景中，通常還會將概率非線性轉化為更為直觀的整數分score=A-B*ln(odds)，方便評分卡更直觀、統一的應用。）
train_prob = lr.predict_proba(data_tr_woe.drop(['isDefault'],axis=1))[:,1]
test_prob = lr.predict_proba(data_test_woe)[:,1]
# Group the predicted scores in bins with same number of samples in each (i.e. "quantile" binning)
toad.metrics.KS_bucket(train_prob, data_tr_woe['isDefault'], bucket=10, method = 'quantile')當預測這用戶的概率大於設定阈值，意味這個用戶的違約概率很高，就可以拒絕他的貸款申請。
往期精彩回顧
適合初學者入門人工智能的路線及資料下載(圖文+視頻)機器學習入門系列下載中國大學慕課《機器學習》（黃海廣主講）機器學習及深度學習筆記等資料打印《統計學習方法》的代碼復現專輯機器學習交流qq群955171419，加入微信群請掃碼
