List of articles
effect
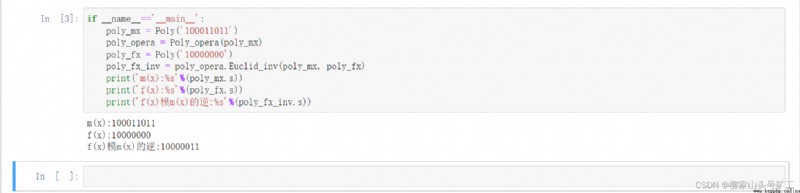
Code
import pandas as pd
class Poly():
def __init__(self, s: str):
self.s = s
self.poly, self.length = self.__str2poly(s)
# target: Receive string , Return to its list form
# params: character string
# return: String list form and its length
def __str2poly(self, s: str)-> list:
return list(pd.Series(list(s)).map(int)), len(s)
class Poly_opera():
def __init__(self, mx):
self.mx = mx
self .m = self.add(self.mx, Poly(''.join(['1',*((self.mx.length-1) * ['0'])])))
# target: Set up mx
# params: mx
# return: nothing
def set_mx(self, mx):
self.mx = mx
self .m = self.add(self.mx, Poly(''.join(['1',*((self.mx.length-1) * ['0'])])))
# target: Add two polynomials
# params: polynomial 0, polynomial 1
# return: Sum of polynomials
def add(self, poly0, poly1):
poly0_lt = poly0.poly
poly1_lt = poly1.poly
align_lt = [0] * abs(poly0.length-poly1.length)
if(poly0.length-poly1.length>=0):
align_lt.extend(poly1_lt)
poly1_lt = align_lt
else:
align_lt.extend(poly0_lt)
poly0_lt = align_lt
xor_res_lt = list((pd.Series(poly0_lt) ^ pd.Series(poly1_lt)).map(str))
return Poly(str(int(''.join(xor_res_lt))))
# target: Calculation poly0 And x^i The product of the
# params: poly0
# return: poly0 And x^i List of product polynomials
def __single_multi(self, poly0):
ret = [poly0]
for i in range(self.mx.length-2):
if(ret[-1].length==self.mx.length-1):
temp_poly_s = Poly(ret[-1].s[1:] + '0')
ret.append(self.add(temp_poly_s, self.m))
else:
temp_poly_s = Poly(ret[-1].s[:] + '0')
ret.append(temp_poly_s)
return ret
# target: Calculation poly0 And poly0 The product of the
# params: poly0,poly1
# return: Product of two polynomials
def multi(self, poly0, poly1):
poly1_lt = poly1.poly.copy()
poly1_lt.reverse()
poly0_single = self.__single_multi(poly0)
ret = Poly('0')
for i in range(len(poly1_lt)):
if(poly1_lt[i]==1):
ret = self.add(ret, poly0_single[i])
return ret
# target: Polynomial division
# paramas: Divisor , Divisor
# return: Quotient and remainder
def div(self, poly_divisor, poly_dividend):
dic_ = {
}
while(poly_divisor.s!='0' and poly_divisor.length >= poly_dividend.length):
extend_length = poly_divisor.length - poly_dividend.length
extend_dividend = Poly(poly_dividend.s + ''.join(['0'] * extend_length))
poly_divisor = self.add(poly_divisor, extend_dividend)
dic_[extend_length+1] = 1
res = []
dic_keys = list(dic_.keys())
for i in range(1, dic_keys[0]+1):
if(i in dic_keys):
res.insert(0, '1')
else:
res.insert(0, '0')
return Poly(''.join(res)), poly_divisor
# target: division
# params: Divisor , Divisor
# return: Quotient and remainder
def get_QR(self, poly_divisor, poly_dividend):
Q_lt = []
R_lt = []
while(poly_dividend.s != '0'):
poly_Q, poly_R = self.div(poly_divisor, poly_dividend)
Q_lt.append(poly_Q)
R_lt.append(poly_R)
poly_divisor = poly_dividend
poly_dividend = poly_R
return Q_lt, R_lt
# target: Finding the inverse of a polynomial ( Prerequisite :gcd(mx,fx)=1)
# paramas: mx,fx
# return: fx mod mx The inverse of
def Euclid_inv(self, poly_mx, poly_fx):
Q_lt, R_lt = self.get_QR(poly_mx, poly_fx)
mx_inv = Poly('1')
fx_inv = Poly('0')
Q_lt.reverse()
R_lt.reverse()
for q, r in zip(Q_lt, R_lt):
mx_inv, fx_inv = fx_inv, self.add(mx_inv, self.multi(q, fx_inv))
return fx_inv
if __name__=='__main__':
poly_mx = Poly('100011011')
poly_opera = Poly_opera(poly_mx)
poly_fx = Poly('10000000')
poly_fx_inv = poly_opera.Euclid_inv(poly_mx, poly_fx)
print('m(x):%s'%(poly_mx.s))
print('f(x):%s'%(poly_fx.s))
print('f(x) model m(x) The inverse of :%s'%(poly_fx_inv.s))
