Abstract : This paper introduces two coding methods, cyclic code and convolutional code , also , The author gives the coding and decoding of two coding methods python Realization
keyword : Cyclic code , System code , Convolutional code ,python,Viterbi Algorithm
set up \(C\) It's a \(q\) element \([n,n-r]\) Cyclic code , Its generating polynomial is \(g(x), \text{deg}(g(x))=r\). obviously ,\(C\) Yes \(n-r\) Two information bits ,\(r\) Check bits . We use it \(C\) For information sources \(V(n-r,q)\) Is represented by a vector in .
For any information source vector \(a_0a_1\cdots a_{n-r-1}\in V(n-r,q)\), There are two coding ideas for cyclic codes :
Construct information polynomial
\[a(x) = a_0+a_1x+\cdots+a_{n-r-1}x^{n-r-1} \]The polynomial of the information source corresponds to the cyclic code \(C\) A codeword of
\[c(x)=a(x)g(x) \]Construct information polynomial
\[\bar{a}(x)=a_0x^{n-1}+a_1x^{n-2}+\cdots+a_{n-r-1}x^r \]Obviously \(a_0,a_1,\cdots,a_{n-r-1}\) When not all are zero .\(r\lt\text{deg}(\bar{a}(x))=n-1\). use \(g(x)\) Remove \(\bar{a}(x)\), obtain
\[\bar{a}(x)=q(x)g(x)+r(x) \]among \(\text{deg}(r(x))\lt\text{deg}(g(x))=r\), The information source polynomial is encoded as C Code words in
\[c(x)=q(x)g(x)+r(x)=\bar{a}(x)-r(x) \]You can see ,\(\bar{a}(x)\) and \(r(x)\) , There are no identical items , So this coding method is system coding . That is to say , If you will \(c(x)\) Medium \(x\) The items of are sorted by birth order , Before the code word \(n-r\) Bits are information bits , after \(r\) Bit is check bit .
It is known that \(C\) It's a binary \((7,4)\) Cyclic code , The resulting polynomial is \(g(x)=x^3+x+1\).
\(0101\in V(4,2)\) Is the information vector of the generation code
That is to say ,\(0101\in V(4,2)\) Encoded as \(0111001\in V(7,2)\)
That is to say ,\(0101\in V(4,2)\) Encoded as \(0101100\in V(7,2)\)
generally speaking , The decoding speed of system code is faster than that of non system code . Next, let's explore the above examples further .
consider \(F_2[x]/\langle x^7-1\rangle\) The medium order is greater than 3 Base .
\[f_1(x)=x^6=(x^3+x+1)(x^3+x+1)+x^2+1 \]That is to say ,\(1000\in V(4,2)\) Encoded as \(1000101\in V(7,2)\).
\[f_2(x)=x^5=(x^2+1)(x^3+x+1)+x^2+x+1 \]That is to say ,\(0100\in V(4,2)\) Encoded as \(0100111\in V(7,2)\).
\[f_3(x)=x^4=x(x^3+x+1)+x^2+x \]That is to say ,\(0010\in V(4,2)\) Encoded as \(0010110\in V(7,2)\).
\[f_4(X)=x^3=(x^3+x+1)+x+1 \]That is to say ,\(0001\in V(4,2)\) Encoded as \(0001011\in V(7,2)\).
So the generated polynomial is \(g(x)=x^3+x+1\) Of \((7,4)\) Cyclic code C The generating matrix of is
\[G= \begin{bmatrix} 1 & 0 & 0 & 0 & \vdots &1&0&1 \\ 0 & 1 & 0 & 0 & \vdots &1&1&1 \\ 0 & 0 & 1 & 0 & \vdots &1&1&0 \\ 0 & 0 & 0 & 1 & \vdots &0&1&1 \\ \end{bmatrix} \]First, we introduce the knowledge of the check matrix of the check polynomial kernel of the cyclic matrix without proof .
Definition set up \(C\subset R_n\) It's a \(q\) element \([n,n-r]\) Cyclic code , Its generating polynomial is \(g(x)\), The check polynomial is defined as
\[h(x)\triangleq(x^n-1)/g(x) \]Theorem set up \(C\subset R_n\) It's a \(q\) element \([n,n-r]\) Cyclic code , Its generating polynomial is \(g(x)\), The check polynomial is \(h(x)\), For any \(c(x)\in R_n(x)\),\(c(x)\) yes \(C\) If and only if \(c(x)h(x)=0\).
Theorem set up \(C\subset R_n\) It's a \(q\) element \([n,n-r]\) Cyclic code , Its generating polynomial is \(g(x)\), The check polynomial is written as
\[h(x)=(x^n-1)/g(x)\triangleq h_{n-r}x^{n-r}+\cdots+h_1x+h_0 \]And its check matrix is
\[H= \begin{pmatrix} h_{n-r} & h_{n-r-1} & h_{n-r-2} & \cdots & h_0 & 0 & 0 & \cdots & 0 \\ 0 & h_{n-r} & h_{n-r-1} & h_{n-r-2} & \cdots & h_0 & 0 & \cdots & 0 \\ 0 & 0 & h_{n-r} & h_{n-r-1} & h_{n-r-2} & \cdots & h_0 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & h_{n-r} & h_{n-r-1} & h_{n-r-2} & \cdots &h_0\\ \end{pmatrix} \]So you can get it. , For known \(C\) It's a binary \((7,4)\) Cyclic code , The resulting polynomial is \(g(x)=x^3+x+1\), The check polynomial is \(h(x)=x^4+x^3+x^2+1\), The check matrix is
\[H= \begin{pmatrix} 1 & 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 & 0 & 1 \\ \end{pmatrix} \]Because it is the system code , therefore , If you will \(c(x)\) Medium \(x\) The terms of are sorted to the power of descent , Before the code word \(n-r\) Bits are information bits , after \(r\) Bit is check bit . That is to say , If there is no error , Before the accepted codeword 4 individual '' Letter ''( Information bits ) Is the information transmitted by the other party .
But considering the general situation , The decoding process of binary cyclic code is as follows
For the above codewords , If received \(y=0110010\),\(S(y)=yH^T=011=1*H_4\), So the sending code word is \(0111010\), I.e. information source \(0111\).
For the above cyclic code ,python The program is implemented as follows
# (7,4) Binary cyclic code
# Generating polynomials g(x)= x^3+x+1
import numpy as np
# Generate matrix
G = np.array([
[1,0,0,0,1,0,1],
[0,1,0,0,1,1,1],
[0,0,1,0,1,1,0],
[0,0,0,1,0,1,1]
])
# Check matrix
H = np.array([
[1,1,1,0,1,0,0],
[0,1,1,1,0,1,0],
[0,0,1,1,1,0,1]
])
# code
def encode_cyclic(x):
if not len(x) == 4:
print(" Please enter 4 Bit information bit ")
return
y = np.dot(x,G)
print(x," Encoded as :",y)
return y
# decoding , The process is consistent with Hamming code
def decode_cyclic(y):
if not len(y) == 7:
print(" Please enter 7 Bit information bit ")
return
x_tmp = np.dot(y,H.T)%2
if (x_tmp!=0).any():
for i in range(H.shape[1]):
if (x_tmp==H[:,i]).all():
y[i] = (y[i]-1)%2
break
x = y[0:4]
print(y," Decoding for :",x)
return x
# test
if __name__ == '__main__':
y = [1,0,0,0,1,0,1]
decode_cyclic(y)
x=[1,0,0,0]
encode_cyclic(x)
Convolutional code is one of the channel coding techniques , It belongs to an error correcting code . The earliest by 1955 year Elias Put forward at the earliest , The purpose is to reduce the error caused by the source message in the channel transmission process , Increase the accuracy of receiver decoding .
The convolutional code is generated by passing the information sequence to be transmitted through the linear finite state shift register , That is, in the encoding process of convolutional codes , The input message source needs to be convoluted with the impulse response in the encoder . say concretely , At any time , Encoder \(n\) The output is not only related to the \(k\) Input about , It is also associated with the previous \(m\) Input about . The error correction ability of convolutional codes increases with \(m\) Increase with the increase of , At the same time, the error rate increases with \(m\) The index decreases with the increase of .
Parameters \((n,k,m)\) Explain the following :
It seems , The result of convolutional code coding is related to the previous input , Coding is memory , Yes no block code . The code of the block code is only related to the current input , Coding is not memory .
1967 year Viterbi A maximum likelihood algorithm based on dynamic programming is proposed Viterbi Decoding method .
The picture below shows :(2,1,2) Coding diagram of convolutional code
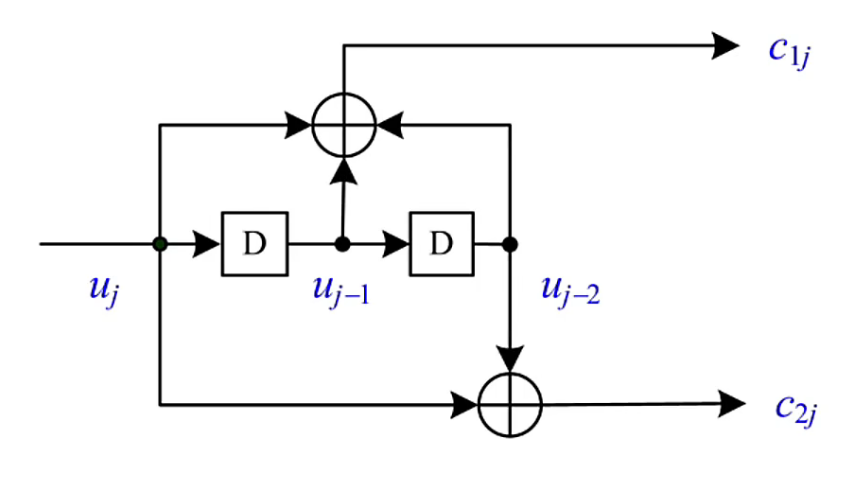
among ,\(j\) Indicates timing ,
\[\begin{aligned} c_{1j} &= u_j+D_1+D_2 = u_j+u_{j-1}+u_{j-2} \\ c_{2j} &= u_j + D_2 = u_j + u_{j-2} \end{aligned} \]In order to explain the important in convolutional codes “ state ” Concept , Now we introduce the mark ( Only with 2 Take output as an example ,\(n\) Outputs can be pushed in this way ):
So it's not hard to see (2,1,2) Convolutional codes consist of 4 All possible states , by \((00),(01),(10),(11)\).
We have the following lemma for states
lemma
Given departure status \(s_{j-1}\) And the current input \(u_j\), The arrival status can be determined \(s_j\) And the current output \(c_{1_j}c_{2j}\)
A sequence of changes in a given state \(s_0s_1s_2\cdots\), It will be possible to determine the input sequence \(u_0u_1u_2\cdots\) And output sequence \(c_{10}c{20}c_{11}c_{21}\cdots\)
notes : We default to the initial state \(s_{-1}=0\)
From the above description , It's not hard to see. , All the information of convolutional codes is contained in the sequence of state changes .
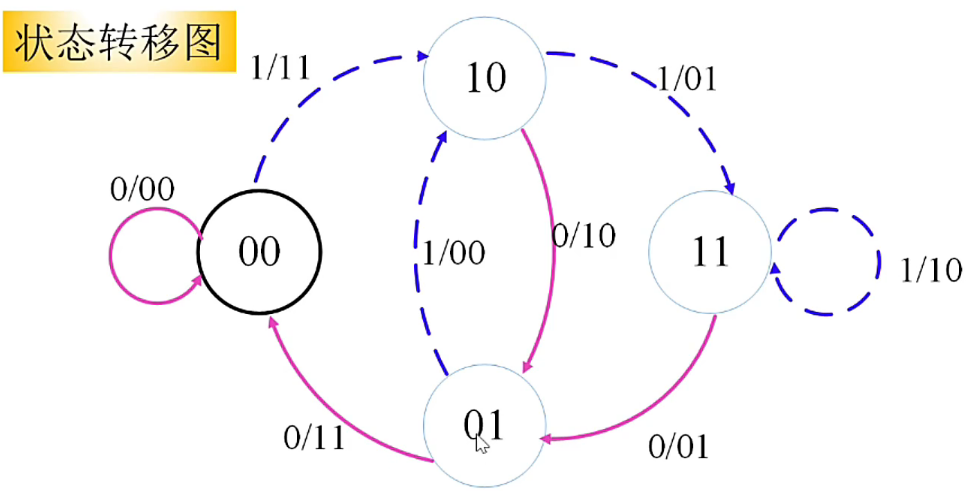
The following figure for “ Gatu ”,
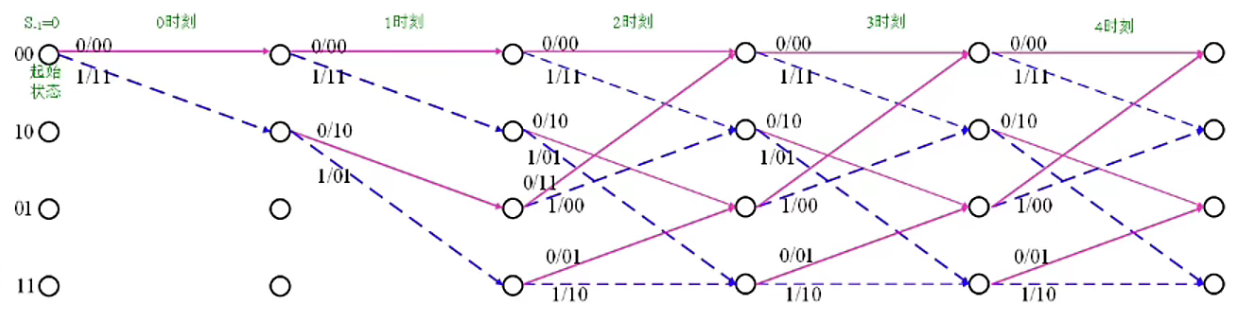
The grid structure is more compact , Represents the movement of time , That is to say , Bits of information are constantly being input .
From the above , We can conclude that , If the input sequence is \(10110\), Then the output sequence is \(11 10 00 01 01\).
The code example is as follows
# (2,1,2) Convolutional code
# Convolutional coding
def encode_conv(x):
# Store encoded information
y = []
# Two registers u_1 u_2 Initialize to 0
u_2 = 0
u_1 = 0
for j in x:
c_1 = (j + u_1 + u_2)%2
c_2 = (j+u_2)%2
y.append(c_1)
y.append(c_2)
# Update register
u_2 = u_1
u_1 = j
print(x," Encoded as :",y)
return y
# Test code
if __name__ == '__main__':
encode_conv([1,0,1,1,0])
We noticed that
set up \(j\) The bits received at any time are \(y_{1j}y_{2j}\)
For example, from the second \(i\) Step to step \((i+1)\) Step received bits \(01\)
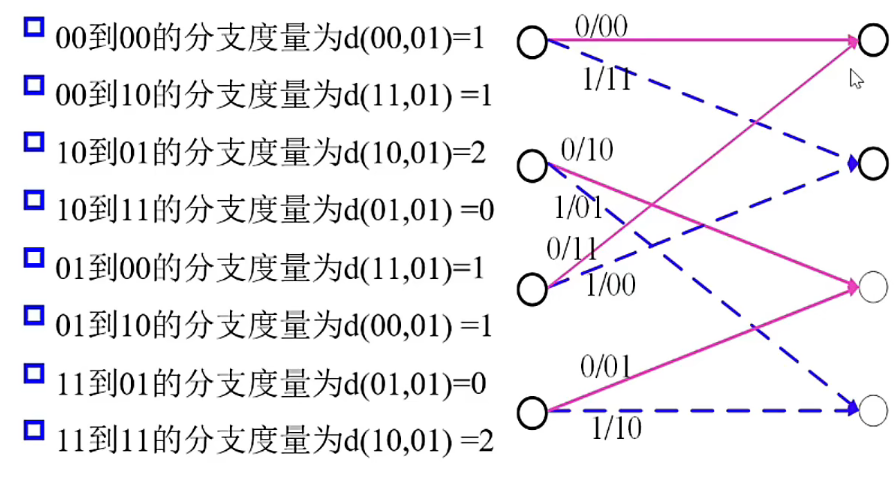
The following are the input bits :01 11 01 Lattice graph of .
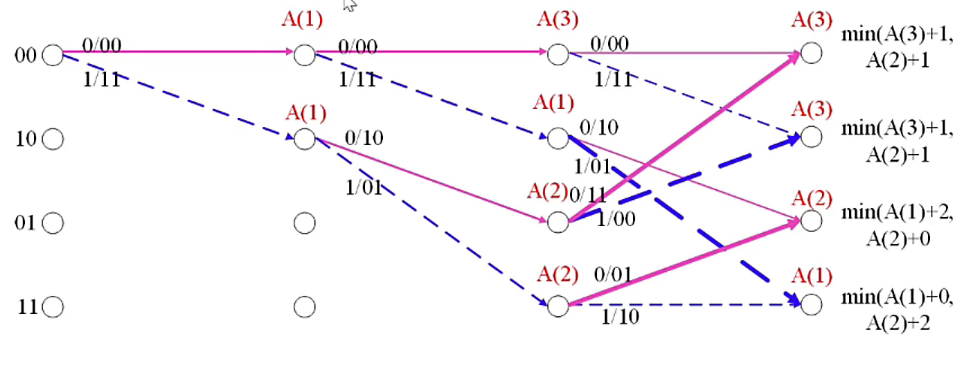
among \(A(i)\) Indicates that the cumulative measurement from the start time to the current time is \(i\)
For the receiving sequence is :01 11 01 11 00
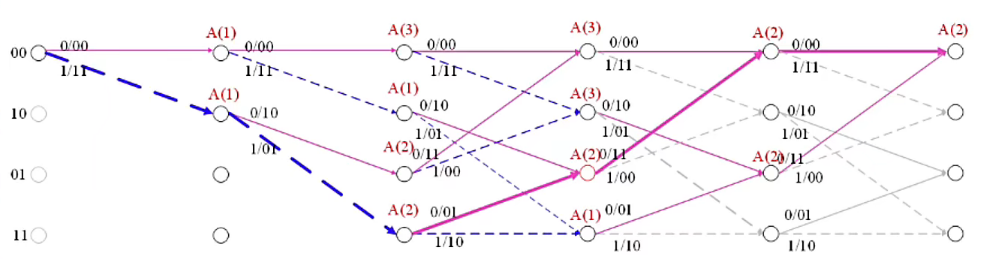
Through the above path analysis diagram, we can get , After maximum likelihood decoding analysis , The decoding sequence is :11000
Viterbi decoding python The implementation is as follows :
def decode_conv(y):
# shape = (4,len(y)/2)
# initialization
score_list = np.array([[ float('inf') for i in range(int(len(y)/2)+1)] for i in range(4)])
for i in range(4):
score_list[i][0]=0
# Record the backtrace path
trace_back_list = []
# Backtracking blocks for each phase
trace_block = []
# 4 States 0-3 They correspond to each other ['00','01','10','11']
states = ['00','01','10','11']
# According to the different state and Input Encoding information
def encode_with_state(x,state):
# Coded output
y = []
u_1 = 0 if state<=1 else 1
u_2 = state%2
c_1 = (x + u_1 + u_2)%2
c_2 = (x + u_2)%2
y.append(c_1)
y.append(c_2)
return y
# Calculate Hamming distance
def hamming_dist(y1,y2):
dist = (y1[0]-y2[0])%2 + (y1[1]-y2[1])%2
return dist
# According to the current state now_state And input information bits input, Figure out the next state
def state_transfer(input,now_state):
u_1 = int(states[now_state][0])
next_state = f'{input}{u_1}'
return states.index(next_state)
# Update parameters according to different initial time
# That is, specify the status as state Parameter update at
# y_block by y Part of , shape=(2,)
# pre_state Indicates the current status to be processed
# index Specify the time to process
def update_with_state(y_block,pre_state,index):
# The input is 0
encode_0 = encode_with_state(0,pre_state)
next_state_0 = state_transfer(0,pre_state)
score_0 = hamming_dist(y_block,encode_0)
# Input is 0, And need to be updated
if score_list[pre_state][index]+score_0<score_list[next_state_0][index+1]:
score_list[next_state_0][index+1] = score_list[pre_state][index]+score_0
trace_block[next_state_0][0] = pre_state
trace_block[next_state_0][1] = 0
# The input is 1
encode_1 = encode_with_state(1,pre_state)
next_state_1 = state_transfer(1,pre_state)
score_1 = hamming_dist(y_block,encode_1)
# Input is 1, And need to be updated
if score_list[pre_state][index]+score_1<score_list[next_state_1][index+1]:
score_list[next_state_1][index+1] = score_list[pre_state][index]+score_1
trace_block[next_state_1][0] = pre_state
trace_block[next_state_1][1] = 1
if pre_state==3 or index ==0:
trace_back_list.append(trace_block)
# The default register is initially 00. That is to say , Starting time , The default state is 00
# Start the first one y_block Update
y_block = y[0:2]
trace_block = [[-1,-1] for i in range(4)]
update_with_state(y_block=y_block,pre_state=0,index=0)
# After the start y_block to update
for index in range(2,int(len(y)),2):
y_block = y[index:index+2]
for state in range(len(states)):
if state == 0:
trace_block = [[-1,-1] for i in range(4)]
update_with_state(y_block=y_block,pre_state=state,index=int(index/2))
# Complete the forward process , Start backtracking
# state_trace_index Express What is the status of starting backtracking
state_trace_index = np.argmin(score_list[:,-1])
# Record the original coding information
x = []
for trace in range(len(trace_back_list)-1,-1,-1):
x.append(trace_back_list[trace][state_trace_index][1])
state_trace_index = trace_back_list[trace][state_trace_index][0]
x = list(reversed(x))
print(y," Decoding for :",x)
return x
# Test code
if __name__ == '__main__':
# Corresponding 1 1 0 0 0
decode_conv([0,1,1,1,0,1,1,1,0,0])
Reference resources
(7,3) Cyclic code coding and decoding C Realization
Convolutional coding and Viterbi decoding - mdnice Ink drop
Noisy channel coding — Linear block code _ Bili, Bili _bilibili