資源下載地址:https://download.csdn.net/download/sheziqiong/85695269
資源下載地址:https://download.csdn.net/download/sheziqiong/85695269
目錄
1求解多極小函數 2
1.1SA 算法 2
1.1.1算法流程 2
1.1.220 次隨機實驗的統計結果 3
1.1.3目標函數的變化曲線 3
1.2GA 算法 6
1.2.1編碼 6
1.2.2算法流程 6
1.2.3算法參數 7
1.2.420 次隨機實驗的統計結果 7
1.2.5目標函數的變化曲線 7
2TSP 問題 8
2.1SA 算法 8
2.1.1算法流程 8
2.1.220 次隨機實驗的統計結果 8
2.2GA 算法 13
2.2.1 編碼 13
2.2.2算法流程 13
2.2.3算法參數 13
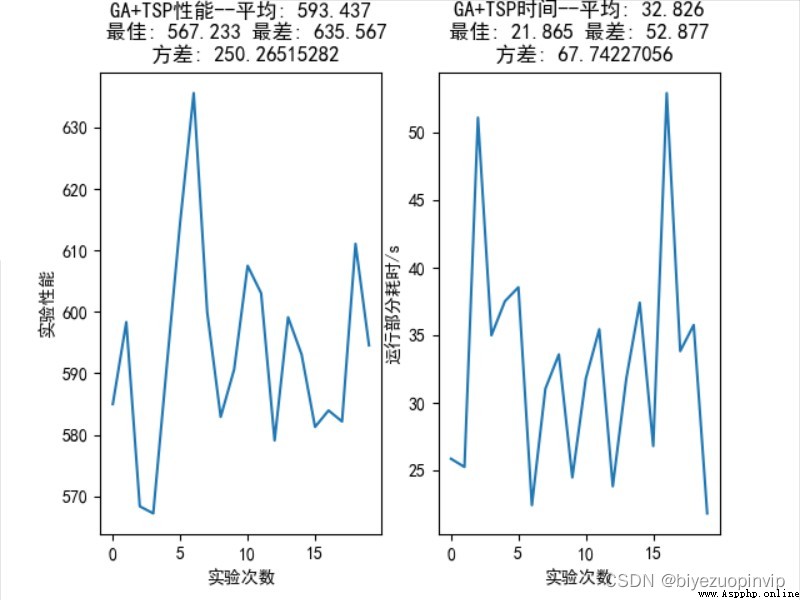
2.2.420 次隨機實驗的統計結果 13
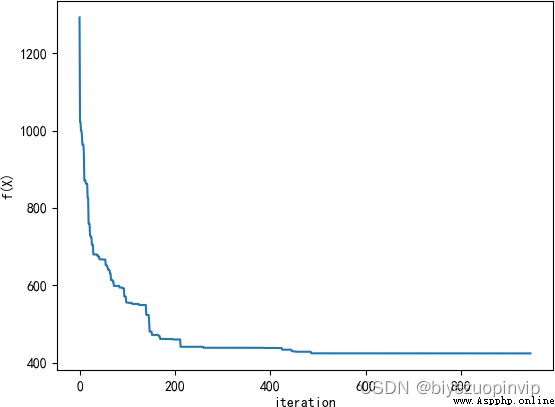
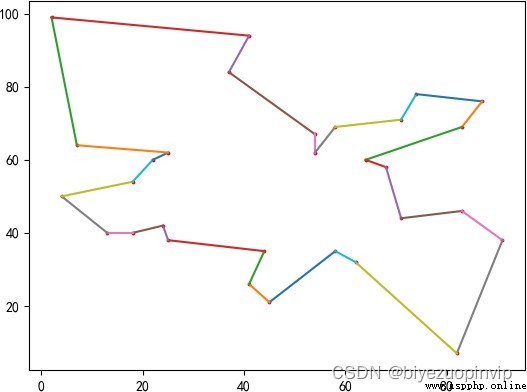
2.2.5一次實驗結果 13
3算法特點 17
3.1 SA 17
3.2 GA 17
4TSP 可視化應用程序 17
5實驗分工 18
1求解多極小函數
求解多極值函數問題中,我們需要求出函數的最值,我們以函數 f (x0, x1) = −x1 ∗ sin(x0) −
x0 ∗ cos(x1) 為例,求它在 x0, x1 ∈ [−10, 10] 區間內的最小值。
使用 MATLAB 畫出的函數圖像如圖1所示,其最小值可用 matlab 庫函數求出,約為-17.394, 同時該函數有多個局部極小值。
算法流程與上文基本類似,不同之處在於:
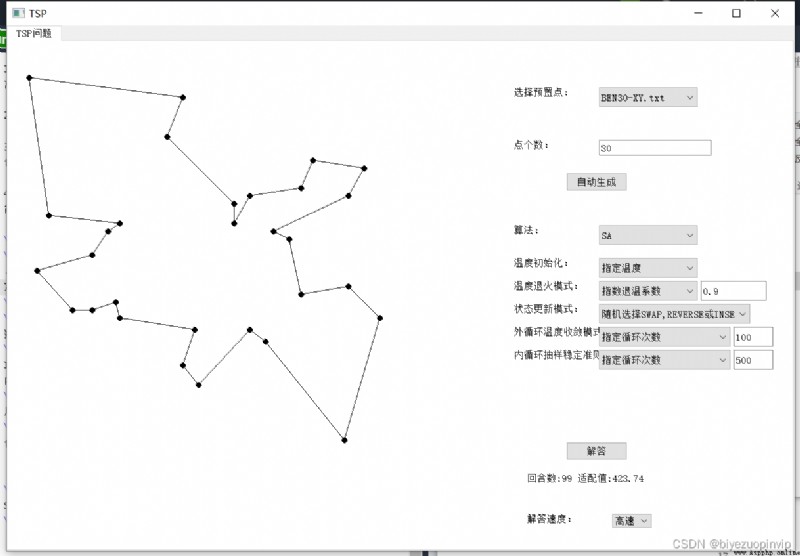
步驟 1 中,初始溫度可以有兩種生成方式:按照經驗設定固定初溫要更大,隨機選擇指定數量計算方差時指定的元素數目也大得多;初始解在離散的 TSP 問題中為旅行商所經城市的路線。
步驟 4 為狀態更新,在 TSP 問題中,可以通過進行兩位置元素交換、兩位置之間的元素逆序、把指定某一段序列插到第三個位置之後或者把上述操作按照概率混合的方法產生新的狀態, 即新的旅行商路線。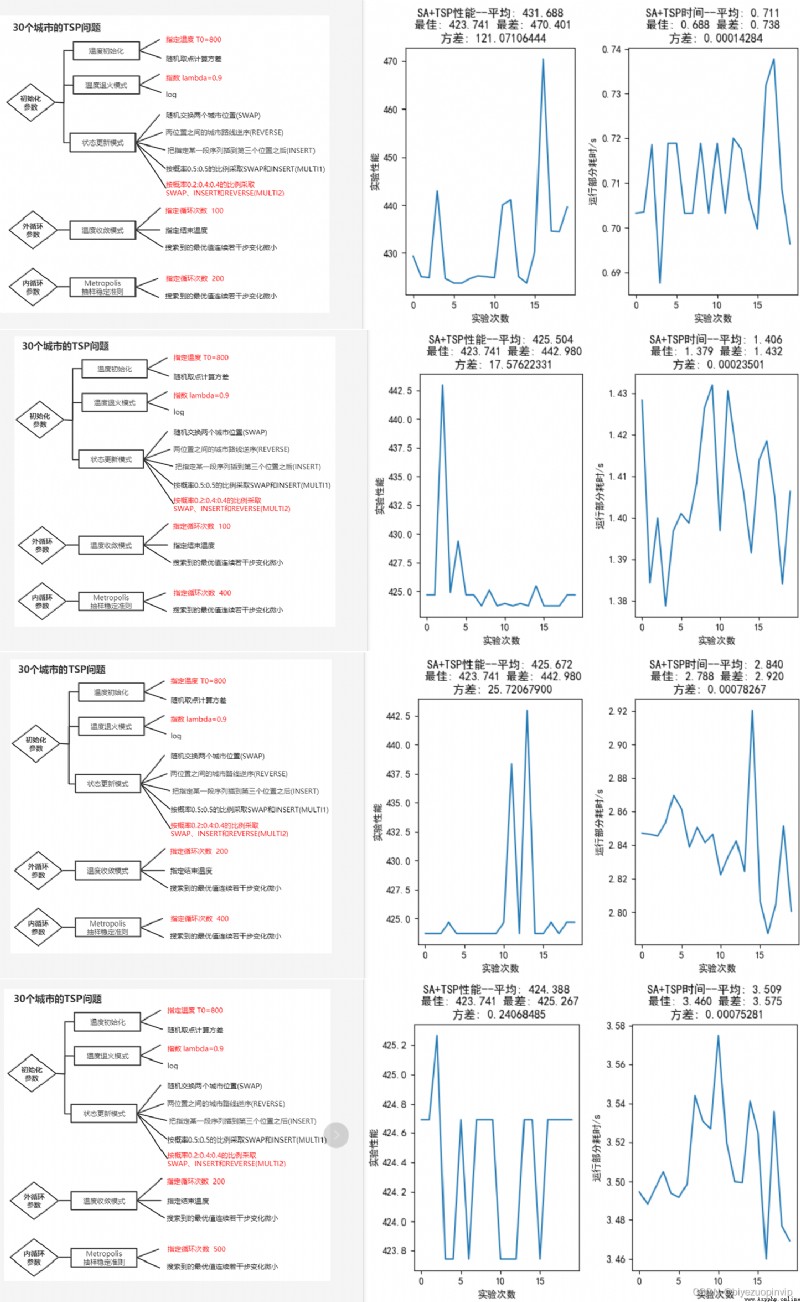
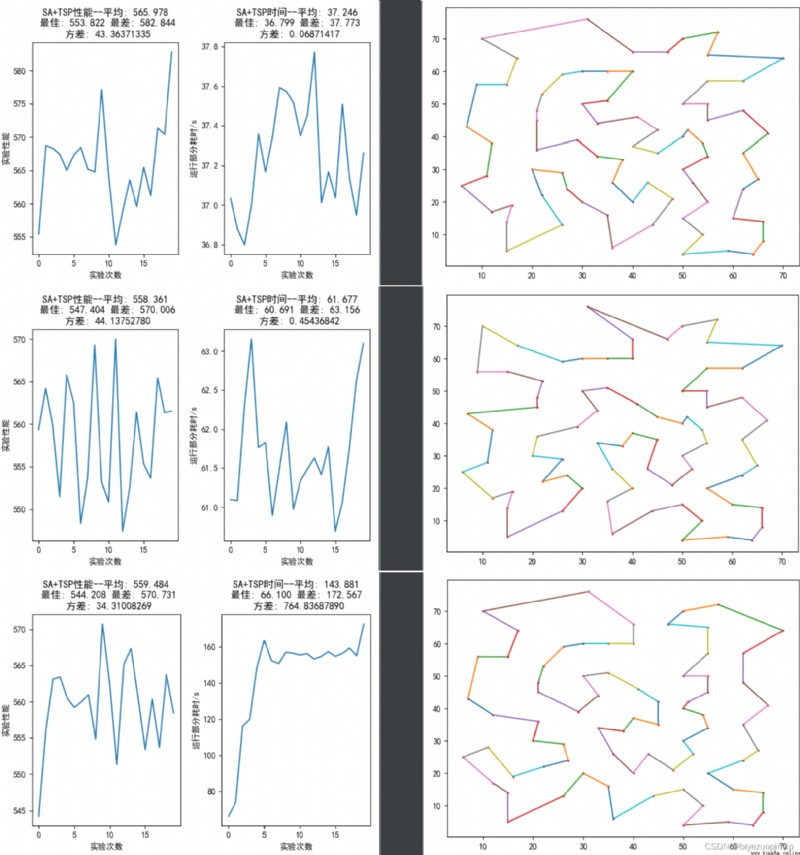
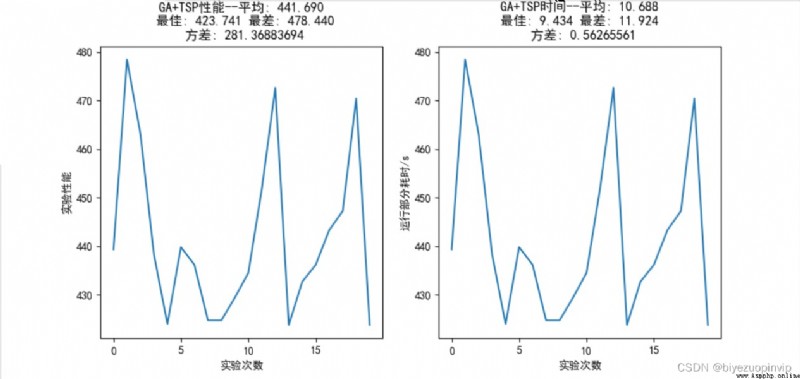
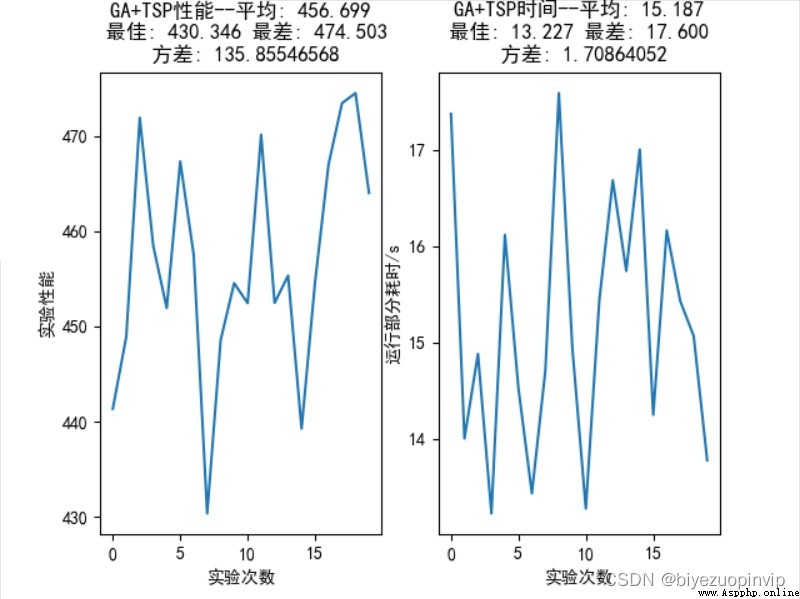

資源下載地址:https://download.csdn.net/download/sheziqiong/85695269
資源下載地址:https://download.csdn.net/download/sheziqiong/85695269