偶然發現linux系統附帶的一個數獨游戲,打開玩了幾把。無奈是個數獨菜鳥,以前沒玩過,根本就走不出幾步就一團漿糊了。
於是就打算借助計算機的強大運算力來暴力解數獨,還是很有樂趣的。
下面就記錄一下我寫解數獨程序的一些思路和心得。
一.數獨游戲的基本解決方法
編程籠統的來說,就是個方法論。不論什麼程序,都必須將問題的解決過程分解成計算機可以實現的若干個簡單方法。俗話說,大道至簡。對於只能明白0和1的計算機來說,就更需要細分步驟,一步一步的解決問題了。
首先來思考一下解數獨的基本概念。
數獨橫九豎九共八十一個格子,同時又分為9個九宮格。規則很簡單——需要每一個格中的數字,都保證與其所在橫排和豎排以及九宮格內無相同數字。
所以我們的大概思路就是,從第一個空格開始試著填數,從 1 開始填,如果 1 不滿足橫排豎排九宮格無重復的話,就再填入 2 ,以此類推,直到填入一個暫時滿足規則的數,中斷此格,移動到下一個空格重復這個過程。
如果到達某個空格發現已經無數可選了,說明前面某一格填錯了,那就返回上一格,從上一格的中斷處繼續往 9 嘗試,直到這樣回朔到填錯的那一格。
這樣的話,我們就可以整理出重要的步驟了:
•尋找到下一個空格
•輪流填入格中數字 1 到 9
•遞歸判斷填入數是否符合規則
二.程序
首先測試數獨使用的是芬蘭數學家因卡拉花費3個月時間設計出的世界上迄今難度最大的數獨。如下
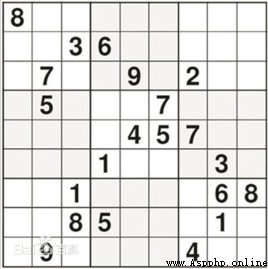
將空格用 0 表示,同時將數獨表示成嵌套的列表,這樣每格的行數和列數就正好是列表中每個對應數的索引。
程序如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#coding=utf-8
import datetime
class solution(object):
def __init__(self,board):
self.b = board
self.t = 0
def check(self,x,y,value):#檢查每行每列及每宮是否有相同項
for row_item in self.b[x]:
if row_item == value:
return False
for row_all in self.b:
if row_all[y] == value:
return False
row,col=x/3*3,y/3*3
row3col3=self.b[row][col:col+3]+self.b[row+1][col:col+3]+self.b[row+2][col:col+3]
for row3col3_item in row3col3:
if row3col3_item == value:
return False
return True
def get_next(self,x,y):#得到下一個未填項
for next_soulu in range(y+1,9):
if self.b[x][next_soulu] == 0:
return x,next_soulu
for row_n in range(x+1,9):
for col_n in range(0,9):
if self.b[row_n][col_n] == 0:
return row_n,col_n
return -1,-1 #若無下一個未填項,返回-1
def try_it(self,x,y):#主循環
if self.b[x][y] == 0:
for i in range(1,10):#從1到9嘗試
self.t+=1
if self.check(x,y,i):#符合 行列宮均無條件 的
self.b[x][y]=i #將符合條件的填入0格
next_x,next_y=self.get_next(x,y)#得到下一個0格
if next_x == -1: #如果無下一個0格
return True #返回True
else: #如果有下一個0格,遞歸判斷下一個0格直到填滿數獨
end=self.try_it(next_x,next_y)
if not end: #在遞歸過程中存在不符合條件的,即 使try_it函數返回None的項
self.b[x][y] = 0 #回朔到上一層繼續
else:
return True
def start(self):
begin = datetime.datetime.now()
if self.b[0][0] == 0:
self.try_it(0,0)
else:
x,y=self.get_next(0,0)
self.try_it(x,y)
for i in self.b:
print i
end = datetime.datetime.now()
print '\ncost time:', end - begin
print 'times:',self.t
return
s=solution([[8,0,0,0,0,0,0,0,0],
[0,0,3,6,0,0,0,0,0],
[0,7,0,0,9,0,2,0,0],
[0,5,0,0,0,7,0,0,0],
[0,0,0,8,4,5,7,0,0],
[0,0,0,1,0,0,0,3,0],
[0,0,1,0,0,0,0,6,8],
[0,0,8,5,0,0,0,1,0],
[0,9,0,0,0,0,4,0,0]])
s.start()
值得注意的是使用的遞歸判斷能夠很巧妙的在走錯分支時回朔到上一層。具體實現是通過 for 循環來從 1 到 9 不斷填入數字同時達到記錄中斷點的作用。通過下一層的返回值來確定是否回朔。
程序輸出如下:
?
1
2
3
4
5
6
7
8
9
10
11
12
[8, 1, 2, 7, 5, 3, 6, 4, 9]
[9, 4, 3, 6, 8, 2, 1, 7, 5]
[6, 7, 5, 4, 9, 1, 2, 8, 3]
[1, 5, 4, 2, 3, 7, 8, 9, 6]
[3, 6, 9, 8, 4, 5, 7, 2, 1]
[2, 8, 7, 1, 6, 9, 5, 3, 4]
[5, 2, 1, 9, 7, 4, 3, 6, 8]
[4, 3, 8, 5, 2, 6, 9, 1, 7]
[7, 9, 6, 3, 1, 8, 4, 5, 2]
cost time: 0:00:00.060687
times: 45360
可以看到程序雖然運算次數比較多,但是速度還是很快的。