By chance linux One attached to the system Sudoku game , Open and play a few . But he is a novice Sudoku , I haven't played before , There is no way to get out of a few steps .
So I plan to solve Sudoku violently with the help of the powerful computing power of the computer , It's still fun .
The following is a record of my thoughts and experiences in writing Sudoku programs .
One . The basic solution to Sudoku
Programming in general , It's a methodology . Whatever the procedure , The problem solving process must be decomposed into several simple methods that can be realized by the computer . It is said that , The greatest truths are the simplest . I can only understand 0 and 1 For your computer , It is more necessary to subdivide the steps , Step by step to solve the problem .
First of all, let's think about the basic concept of Sudoku .
Sudoku has eighty-one grids in total , At the same time, it is divided into 9 Nine squares . The rules are simple —— You need the number in each cell , It is guaranteed that there are no same numbers in the horizontal and vertical rows and the nine palaces .
So our general idea is , Try to fill in the number from the first blank , from 1 Start filling in , If 1 If you don't meet the requirement that there is no repetition in the horizontal and vertical nine palaces , Then fill in 2 , And so on , Until you fill in a number that temporarily satisfies the rule , Break this box , Move to the next space and repeat the process .
If you reach a certain space, you will find that there are countless options , It means that the previous box is filled in incorrectly , Then go back to the previous grid , Continue from the break in the previous box to 9 Try , Until I go back to the wrong box .
In this case , We can sort out the important steps :
• Find the next space
• Fill in the numbers in the box in turn 1 To 9
• Recursively determine whether the filled number conforms to the rule
Two . Program
The first test of Sudoku was conducted by the Finnish mathematician inkara 3 The most difficult Sudoku in the world has been designed in months . as follows
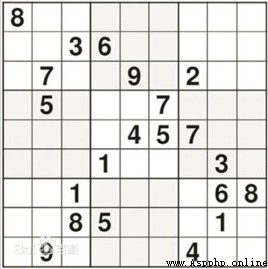
Use spaces with 0 Express , At the same time, Sudoku is represented as a nested list , In this way, the number of rows and columns in each cell is exactly the index of each corresponding number in the list .
The procedure is as follows :
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#coding=utf-8
import datetime
class solution(object):
def __init__(self,board):
self.b = board
self.t = 0
def check(self,x,y,value):# Check whether there are the same items in each row, column and palace
for row_item in self.b[x]:
if row_item == value:
return False
for row_all in self.b:
if row_all[y] == value:
return False
row,col=x/3*3,y/3*3
row3col3=self.b[row][col:col+3]+self.b[row+1][col:col+3]+self.b[row+2][col:col+3]
for row3col3_item in row3col3:
if row3col3_item == value:
return False
return True
def get_next(self,x,y):# Get the next blank
for next_soulu in range(y+1,9):
if self.b[x][next_soulu] == 0:
return x,next_soulu
for row_n in range(x+1,9):
for col_n in range(0,9):
if self.b[row_n][col_n] == 0:
return row_n,col_n
return -1,-1 # If there is no next blank , return -1
def try_it(self,x,y):# Main circulation
if self.b[x][y] == 0:
for i in range(1,10):# from 1 To 9 Try
self.t+=1
if self.check(x,y,i):# accord with The ranks and palaces are unconditional Of
self.b[x][y]=i # Fill in the qualified 0 grid
next_x,next_y=self.get_next(x,y)# Get next 0 grid
if next_x == -1: # If there is no next 0 grid
return True # return True
else: # If there is a next 0 grid , Recursively determine the next 0 Until the Sudoku is filled
end=self.try_it(next_x,next_y)
if not end: # In the recursion process, there are unqualified , namely send try_it The function returns None The item
self.b[x][y] = 0 # Go back to the next level and continue
else:
return True
def start(self):
begin = datetime.datetime.now()
if self.b[0][0] == 0:
self.try_it(0,0)
else:
x,y=self.get_next(0,0)
self.try_it(x,y)
for i in self.b:
print i
end = datetime.datetime.now()
print '\ncost time:', end - begin
print 'times:',self.t
return
s=solution([[8,0,0,0,0,0,0,0,0],
[0,0,3,6,0,0,0,0,0],
[0,7,0,0,9,0,2,0,0],
[0,5,0,0,0,7,0,0,0],
[0,0,0,8,4,5,7,0,0],
[0,0,0,1,0,0,0,3,0],
[0,0,1,0,0,0,0,6,8],
[0,0,8,5,0,0,0,1,0],
[0,9,0,0,0,0,4,0,0]])
s.start()
It is worth noting that the recursive judgment used can skillfully go back to the previous level when the wrong branch is taken . The concrete realization is through for Loop from 1 To 9 Keep filling in numbers and record breakpoints . The return value of the next layer is used to determine whether to go back .
The program output is as follows :
?
1
2
3
4
5
6
7
8
9
10
11
12
[8, 1, 2, 7, 5, 3, 6, 4, 9]
[9, 4, 3, 6, 8, 2, 1, 7, 5]
[6, 7, 5, 4, 9, 1, 2, 8, 3]
[1, 5, 4, 2, 3, 7, 8, 9, 6]
[3, 6, 9, 8, 4, 5, 7, 2, 1]
[2, 8, 7, 1, 6, 9, 5, 3, 4]
[5, 2, 1, 9, 7, 4, 3, 6, 8]
[4, 3, 8, 5, 2, 6, 9, 1, 7]
[7, 9, 6, 3, 1, 8, 4, 5, 2]
cost time: 0:00:00.060687
times: 45360
It can be seen that although the program has a large number of operations , But the speed is still very fast .