Python and fractal 0019 - [tutorial] stack of circles

stack of circles design sketch

STEP 1： Draw a circle

Code ：

turtle.circle(30)

Tulio .

STEP 2： draw 2 layer

design sketch ：

This requires a little mathematical knowledge .

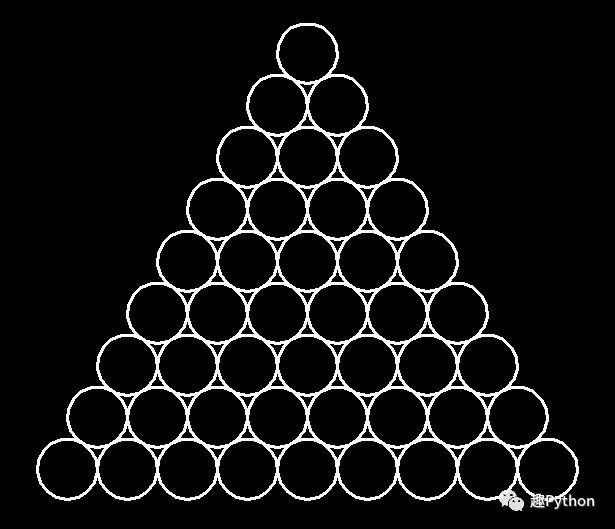
The relative positions of the three circles form an equilateral triangle , Suppose the starting position of the first circle is (x0, y0), that , The starting position of the second circle is (x0-r, y0+sqrt(3)r), The starting position of the third circle is (x0-r+2r,y0+sqrt(3)r).

Knowing the relative position drawing method is simple .

First draw the first circle , The code is ：

r = 30
x0 = 0
y0 = 300
turtle.penup()
turtle.goto(x0, y0)
turtle.pendown()
turtle.circle(r)

Find the starting position of the second circle ：

x0 -= r
y0 -= math.sqrt(3)*r

Draw a second circle ：

turtle.penup()
turtle.goto(x0, y0)
turtle.pendown()
turtle.circle(r)

Draw the third circle ：

turtle.penup()
turtle.goto(x0+2*r, y0)
turtle.pendown()
turtle.circle(r)

Get it done , The sharp eyed students must see that it can be reconstructed , We'll wait .

STEP 2： draw 3 layer

design sketch ：

Already by 1 Layers are derived to 2 layer , that , from 2 Layer derived to 3 The layer is simpler , Add code directly .

x0 -= r
y0 -= math.sqrt(3)*r
turtle.penup()
turtle.goto(x0, y0)
turtle.pendown()
turtle.circle(r)
turtle.penup()
turtle.goto(x0+2*r, y0)
turtle.pendown()
turtle.circle(r)
turtle.penup()
turtle.goto(x0+4*r, y0)
turtle.pendown()
turtle.circle(r)

STEP 3: restructure

We found that ,1->2,2->3 The logic of is the same , The code is basically the same , Refactoring .

def stack_circles(x0, y0, r, stacks):
    turtle.penup()
    turtle.goto(x0, y0)
    turtle.pendown()
    turtle.circle(r)
    if stacks > 1:
        for s in range(1, stacks):
            x0 -= r
            y0 -= math.sqrt(3)*r
            for _ in range(s+1):
                turtle.penup()
                turtle.goto(x0 + 2*_*r, y0)
                turtle.pendown()
                turtle.circle(r)
                turtle.update()

pefect.

video