本文是分兩部分的文章的第二部分,討論如何使用 TDD 在編寫代碼之前編寫 測試,並通過這個過程形成更好的設計。在 第 1 部分 中,我采用後測試開發方 法(在編寫代碼之後編寫測試)編寫了完全數查找程序的一個版本。然後,使用 TDD(在編寫代碼之前編寫測試,這樣就可以用測試驅動代碼的設計)編寫了另一 個版本。在第 1 部分的末尾,我發現我在用來保存完全數列表的數據結構類型方 面犯了一個根本性錯誤:我最初根據直覺選用了 ArrayList,但是後來發現 Set 更合適。我將以這個問題為起點,討論如何改進測試的質量和檢查最終代碼的質 量。
測試質量
使用更好的 Set 抽象的測試見清單 1:
清單 1. 使用更好的 Set 抽象的單元測試
_@Test public void add_factors() {
Set<Integer> expected =
new HashSet<Integer>(Arrays.asList(1, 2, 3, 6));
Classifier4 c = new Classifier4(6);
c.addFactor(2);
c.addFactor(3);
assertThat(c.getFactors(), is(expected));
}
這段代碼測試我的問題領域中最關鍵的部分之一:獲取數字的因子。我希望徹 底地測試這個步驟,因為它是問題中最復雜的部分,所以也是最容易出現錯誤的 。但是,它包含一個笨重的構造:new HashSet(Arrays.asList(1, 2, 3, 6));。 即使有了現代 IDE 支持,這行代碼編寫起來也很別扭:輸入 new,輸入 Has,執 行代碼探察;輸入 <Int,再次執行代碼探察,真是太麻煩了。我要讓它容易 些。
潮濕的測試
Andy Hunt 和 Dave Thomas 所著的 The Pragmatic Programmer提出了許多良 好的編程實踐,其中之一是 DRY(Don't Repeat Yourself,不要重復自己)原則 。這條原則主張從代碼中消除所有重復,因為重復常常會導致錯誤。但是,DRY 不適用於單元測試。單元測試常常需要測試有細微差異的代碼行為,因此涉及到 相似和重復的情況。例如,為了在不同的測試中測試各種情況,常常需要復制粘 貼代碼,以得出 清單 1 中預期的結果 (new HashSet(Arrays.asList(1, 2, 3, 6)))。
對於 TDD,我的經驗規則是測試應該是潮濕的,但是不要濕透。也就是說,測 試中可以有一些重復(而且這是不可避免的),但是不應該創建笨拙的重復結構 。因此,我要重構測試,提供一個 private 輔助方法,用它處理這個常用的創建 語句,見清單 2:
清單 2. 保持測試適當潮濕的輔助方法
private Set<Integer> expectationSetWith(Integer... numbers) {
return new HashSet<Integer>(Arrays.asList(numbers));
}
清單 2 中的代碼能夠讓對因子的所有測試更加簡潔,清單 1 中的測試可以改 寫為清單 3 這樣:
清單 3. 更潮濕的數字因子測試
@Test public void factors_for_6() {
Set<Integer> expected = expectationSetWith(1, 2, 3, 6);
Classifier4 c = new Classifier4(6);
c.calculateFactors();
assertThat(c.getFactors(), is(expected));
}
在編寫測試時,也應該遵守良好的設計原則。測試也是代碼,良好的原則也適 用於測試(盡管原則有所差異)。
邊界條件
在為一些新功能編寫第一個測試時,TDD 鼓勵開發人員編寫失敗的測試。這可 以防止測試意外地通過所有情況,也就是說,測試實際上沒有測試任何東西(同 義反復 測試)。測試還可以檢查您認為正確,但是沒有經過充分測試的行為。這 些測試不一定需要首先采用失敗測試的形式(但是,如果在認為測試應該通過時 測試卻失敗了,這是很有價值的,因為這意味著找到了一個潛在的 bug)。考慮 測試會引導您考慮哪些東西是可測試的。
常常被忽視的一種測試用例是邊界條件:當遇到不正常的輸入時,代碼會做什 麼?圍繞 getFactors() 方法編寫一些測試,可以幫助我們考慮合理和不合理的 輸入可能導致什麼情況。
因此,我要針對感興趣的邊界條件編寫幾個測試,見清單 4:
清單 4. 因子的邊界條件
@Test public void factors_for_100 () {
Classifier5 c = new Classifier5(100);
c.calculateFactors();
assertThat(c.getFactors(),
is(expectationSetWith(1, 100, 2, 50, 4, 25, 5, 20, 10)));
}
@Test(expected = InvalidNumberException.class)
public void cannot_classify_negative_numbers() {
new Classifier5(-20);
}
@Test public void factors_for_max_int() {
Classifier5 c = new Classifier5(Integer.MAX_VALUE);
c.calculateFactors();
assertThat(c.getFactors(), is(expectationSetWith(1, 2147483647)));
}
數字 100 看起來很有意思,因為它有許多因子。通過測試多個不同的數字, 我認識到負數對於這個問題領域是沒有意義的,所以編寫了一個排除負數的測試 (在我糾正它之前,這個測試確實會失敗)。考慮到負數還讓我想到了 MAX_INT :如果系統的用戶需要 long 數字,我的解決方案應該怎麼處理呢?我原來假設 數字是整數,但是需要確保這是有效的假設。
需求收集是 “有損壓縮”
請在身邊找一張圖片或畫。假設這張圖片包含 2 百萬像素。如果把圖片壓縮 到只有 2,000 像素,會發生什麼?它看起來還一樣嗎?(如果它是 Rothko 的畫 ,就有可能看起來一樣,但是這種情況很少見)。通過刪除信息實現的壓縮叫作 有損 壓縮算法。如果要把壓縮版本恢復為 2 百萬像素,就需要填補缺失的像素 。有時候能夠猜測出正確的像素,但是不總是可以。
傳統的 “預先做大量的設計(big design up front)” 需求收集過程就像 是 “有損壓縮”,它不能完全准確地反映應用程序所需的功能。業務分析師不可 能預見到可能出現的所有問題,所以要由開發人員補充細節。開發人員在這方面 表現很差,這導致在需求的定義者和實現者之間爭吵不斷。
敏捷的過程把 “解壓” 過程盡可能延後,讓開發人員身邊總是有人可以回答 “程序實際上應該做什麼” 這個問題,從而緩解需求收集過程中的損失。沒有細 節,就不可能進行設計,所以無論采用什麼設計方法,必須以可行的方法補充在 需求收集和定義過程中損失的細節。
測試邊界條件會迫使開發人員明確考慮自己的假設。在編寫解決方案時,很容 易做出無效的假設。實際上,這正是傳統的需求收集過程的缺點之一 — 無法收 集足夠的細節,所以無法消除不可避免的實現問題。需求收集是一種 有損壓縮。
因為在定義 “軟件必須做什麼” 的過程中忽略了太多細節,所以必須通過某 些機制幫助重現那些必須問的問題,從而充分地理解需求。憑空猜測業務用戶實 際上希望做什麼是很危險的,很可能會猜錯。使用測試研究邊界條件有助於找到 要問的問題,這對於理解需求非常重要。找到要問的問題會提供許多信息,有助 於實現良好的設計。
肯定測試和否定測試
在開始研究完全數問題時,我把它分解為幾個子任務。在編寫測試時,我發現 了另一個重要的子任務。下面是完整的列表:
我需要所求數字的因子。
我需要確定某個數字是不是因子。
我需要決定如何把因子添加到因子列表中。
我需要把因子加起來。
我需要確定某個數字是不是完全數。
還沒有完成的兩個任務是把因子加起來和判斷完全數。這兩個任務很簡單;最 後兩個測試見清單 5:
清單 5. 完全數的最後兩個測試
@Test public void sum() {
Classifier5 c = new Classifier5(20);
c.calculateFactors();
int expected = 1 + 2 + 4 + 5 + 10 + 20;
assertThat(c.sumOfFactors(), is(expected));
}
@Test public void perfection() {
int[] perfectNumbers =
new int[] {6, 28, 496, 8128, 33550336};
for (int number : perfectNumbers)
assertTrue(classifierFor(number).isPerfect());
}
在 Wikipedia 上查找到前幾個完全數之後,我可以編寫一個測試,它檢查實 際上是否可以找到完全數。但是,這還沒有完。肯定測試只是工作的一半兒。還 需要編寫另一個測試,確保不會意外地把非完全數分類為完全數。因此,我編寫 了清單 6 所示的否定測試:
清單 6. 確保完全數分類正確的否定測試
@Test public void test_a_bunch_of_numbers() {
Set<Integer> expected = new HashSet<Integer> (
Arrays.asList(PERFECT_NUMS));
for (int i = 2; i < 33550340; i++) {
if (expected.contains(i))
assertTrue(classifierFor(i).isPerfect());
else
assertFalse(classifierFor(i).isPerfect());
}
}
這段代碼報告我的完全數算法工作正常,但是它非常慢。通過查看 calculateFactors() 方法(清單 7),我可以猜出原因。
清單 7. 最初的 getFactors() 方法
public void calculateFactors() {
for (int i = 2; i < _number; i++)
if (isFactor(i))
addFactor(i);
}
清單 7 中出現的問題與 第 1 部分 中後測試版本中的問題相同:尋找因子的 代碼會一直循環到數字本身。可以通過成對地尋找因子來改進此代碼,這樣就只 需要循環到數字的平方根,重構的版本見清單 8:
清單 8. calculateFactors() 方法的性能更好的重構版本
public void calculateFactors() {
for (int i = 2; i < sqrt(_number) + 1; i++)
if (isFactor(i))
addFactor(i);
}
public void addFactor(int factor) {
_factors.add(factor);
_factors.add(_number / factor);
}
這與在後測試版本中做過的重構相似(見 第 1 部分),但是這一次要修改兩 個不同的方法。這裡的修改更簡單,因為我已經把 addFactors() 功能放在一個 單獨的方法中了,而且這個版本使用 Set 抽象,這樣就不需要通過測試確保沒有 出現在後測試版本中曾經出現的重復。
優化的指導原則應該總是先確保它正確,然後加快它的運行速度。全面的單元 測試集能夠輕松地檢查行為是否正確,讓開發人員能夠專心地優化代碼,而不必 擔心是否會破壞代碼的正常行為。
最後,完成了完全數查找程序的測試驅動版本;完整的類見清單 9:
清單 9. 數字分類程序的完整 TDD 版本
public class Classifier6 {
private Set<Integer> _factors;
private int _number;
public Classifier6(int number) {
if (number < 1)
throw new InvalidNumberException(
"Can't classify negative numbers");
_number = number;
_factors = new HashSet<Integer>();
_factors.add(1);
_factors.add(_number);
}
private boolean isFactor(int factor) {
return _number % factor == 0;
}
public Set<Integer> getFactors() {
return _factors;
}
private void calculateFactors() {
for (int i = 2; i < sqrt(_number) + 1; i++)
if (isFactor(i))
addFactor(i);
}
private void addFactor(int factor) {
_factors.add(factor);
_factors.add(_number / factor);
}
private int sumOfFactors() {
int sum = 0;
for (int i : _factors)
sum += i;
return sum;
}
public boolean isPerfect() {
calculateFactors();
return sumOfFactors() - _number == _number;
}
}
可組合的方法
第 1 部分 中提到的測試驅動開發的好處之一是可組合性,也就是采用 Kent Beck 提出的組合方法模式。組合方法可以用許多內聚的方法構建軟件。TDD 能夠 促進這種做法,因為為了進行測試,必須把軟件分解為小的功能塊。組合方法生 成可重用的構建塊,有助於產生更好的設計。
在 TDD 驅動的解決方案中,方法的數量和名稱反映了這種思想。下面是 TDD 完全數分類程序的最終版本中的方法:
isFactor()
getFactors()
calculateFactors()
addFactor()
sumOfFactors()
isPerfect()
下面通過一個示例說明組合方法的好處。假設您已經編寫了完全數查找程序的 TDD 版本,而您公司中的另一個開發組編寫了完全數查找程序的後測試版本(第 1 部分 中有一個示例)。現在,您的用戶慌慌張張地跑來說,“我們還必須判斷 盈數和虧數!” 盈數 的因子的總和大於數字本身,而虧數 的因子的總和小於數 字本身。
在後測試版本中,所有邏輯都放在一個方法中,他們必須重寫整個解決方案, 把盈數、虧數和完全數都涉及的代碼分離出來。但是,對於 TDD 版本,只需要編 寫兩個新方法,見清單 10:
清單 10. 支持盈數和虧數
public boolean isAbundant() {
calculateFactors();
return sumOfFactors() - _number > _number;
}
public boolean isDeficient() {
calculateFactors();
return sumOfFactors() - _number < _number;
}
這兩個方法所需的惟一任務是把 calculateFactors() 方法重構為類的構造函 數。(這對於 isPerfect() 方法沒有害處,但是現在它在所有三個方法中重復出 現,因此應該重構)。
把代碼編寫成小的構建塊會提高代碼的可重用性,因此這是您應該遵守的主要 設計原則之一。使用測試有助於編寫可組合的方法,能夠改進設計。
度量代碼質量
在 第 1 部分 開頭,我指出代碼的 TDD 版本比後測試版本更好。我已經給出 了許多證據,但是能夠進行客觀的證明嗎?當然,對於代碼質量,沒有純粹客觀 的度量方法,但是有幾個指標能夠比較客觀地反映代碼質量;其中之一是圈復雜 度,這是由 Thomas McCabe 發明的度量代碼復雜度的方法。公式非常簡單:邊數 減去節點數,再加 2,這裡的邊代表執行路徑,節點代表代碼行數。請考慮清單 11 中的代碼:
清單 11. 用於判斷圈復雜度的簡單 Java 方法
public void doit() {
if (c1) {
f1();
} else {
f2();
}
if (c2) {
f3();
} else {
f4();
}
}
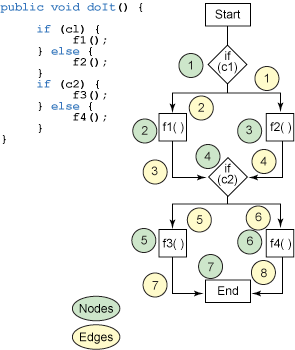
如果把 清單 11 所示的方法畫成流程圖(見圖 1),就很容易算出邊數和節 點數並計算出圈復雜度。這個方法的圈復雜度是 3 (8 - 7 + 2)。
圖 1. doit() 方法的節點和邊
為了度量完全數代碼的兩個版本,我將使用開放源碼的 Java 圈復雜度工具 JavaNCSS(“NCSS” 代表 “non-commenting source statements”,這意味著 這個工具也度量非注釋源代碼語句)。
對後測試代碼運行 JavaNCSS 會產生圖 2 所示的結果:
圖 2. 後測試完全數查找程序的圈復雜度
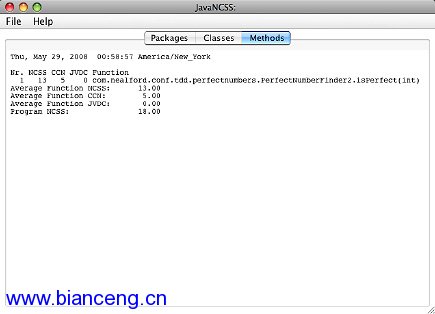
這個版本中只有一個方法,JavaNCSS 報告類的方法平均有 13 行代碼,圈復 雜度為 5.00。TDD 版本的結果見圖 3:
圖 3. 完全數查找程序的 TDD 版本的圈復雜度
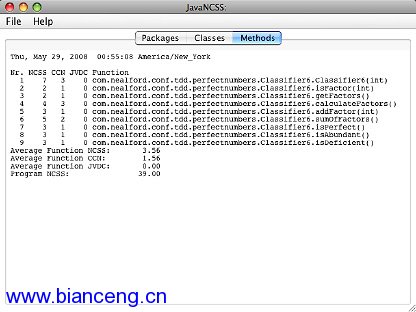
顯然,代碼的 TDD 版本包含更多方法,每個方法平均有 3.56 行代碼,平均 圈復雜度只有 1.56。根據這個指標,TDD 版本比後測試代碼簡單三倍。即使對於 這個小問題,這也是很顯著的差異。
結束語
在 演化架構與緊急設計 系列的最近兩篇文章中,我深入討論了在編寫代碼之 前 編寫測試的好處。TDD 能夠產生更簡單的方法,更好的抽象,可重用性更好的 構建塊。
測試可以引導開發人員沿著更好的設計路徑前進,糾正可能出現的偏差。設計 人員的主觀臆斷可能對設計產生嚴重損害。應該盡可能避免猜想,避免意外地做 出錯誤的決策,但是這很困難。TDD 提供一種有效的習慣性方法,能夠幫助開發 人員跳出錯誤的猜想,克服各種困難順利地設計出解決方案。
在下一篇文章中,我要暫時把測試放在一邊,談談從 Smalltalk 領域借用的 兩個重要模式:組合方法和單一抽象層 原則。