導論
前面我們了解了Robocode中的絕對方向,相對方向及整個方向系統。相信大 家對此深有體會了。但是問題又來了,單知道方向似乎不能完全達到了解敵人的 目的。怎樣去探測敵人的距離?怎樣精確的鎖定目標呢?對於移動中的目標我們 又如何處理?在這裡我們將利用Java.lang 基本類庫中的Math類及一些基本三角 函數方法為你揭開這些迷霧。對於那些快被遺忘的三角幾何知識在本文的最後 Skyala.Li有比較詳細的講解。
坐標基本概念
首先我們還是來看看Robocode API中的一段文字翻譯。
All coordinates are expressed as (x,y).
所有的坐標都用x,y來表示
All coordinates are positive.
所有的坐標都為正
The origin (0,0) is at the bottom left of the screen.
坐標原點(0,0)在屏幕的左下角
Positive x is right. X的右邊為正
Positive y is up. Y的上面為正
圖1顯示了Robocode中的坐標系統,有關圖的詳細說明請看我們前面介紹的文 章 “Robocode基本原理之方向剖析”.
圖1
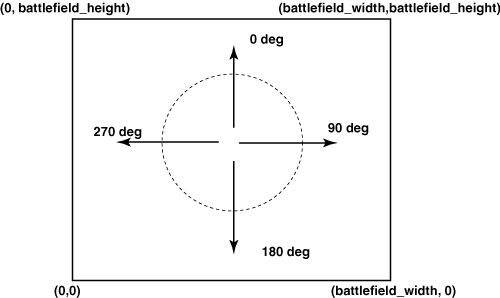
“動靜機器人”測試法
好了,我們知道了Robocode整個坐標系統,一切問題都好辦了。先讓我們進 行一些有趣的實驗。我們仍以”動靜機器人”的方法進行測試。這是個測試機器 人方向,坐標參數的很好辦法。見下說明:
設計兩個機器人,任意取名為Geny和GenyTrack。Geny是個靜止的機器人,它 主要任務是打印自己的當前坐標,用來驗證GenyTrack追蹤它的位置是否正確。 GenyTrack顧名思義,它就是我們要研究的追蹤目標機器人了。它在此負責鎖定 Geny的坐標,距離並打印出探測到的Geny機器人的X,Y坐標及距離,此處使用了 Java.lang類庫中的Math.round方法,四捨五入得到的double類型的數據,方便對 比。最後用表格對比,以此來驗證我們使用方法的正確性。
當然還有很多有趣的測試方法來等待著你的驗證。如測速度,加速度時我們 就可用”龜兔賽跑”的方法;測炮管,雷達坦克車旋轉相互影響度可用”離心重 力”的方法。相信從測試方法的名字聰明的你們就知道他的用法了。
在我們開始前,Skyala.Li建議你們下載源碼( resource)先看看GenyTrack的 表演。當然你也可參考文章內附加的輔助說明Robocode坐標系統的代碼。
Geny:
package test;
import robocode.*;
public class Geny extends AdvancedRobot
{
public void run ()
{
while (true)
{
// round 對get到的數據進行四捨五入處理
out.println("x:"+Math.round(getX()));
out.println("y:"+Math.round(getY()));
}
}
}
GenyTrack:
package test;
import robocode.*;
public class GenyTrack extends AdvancedRobot
{
public void run ()
{
while (true)
{
turnRadarRight(400);
}
}
public void onScannedRobot(ScannedRobotEvent e)
{
double bearing = (getHeading() + e.getBearing()) % 360;
double distance = e.getDistance();
bearing = Math.toRadians(bearing);
double genyX = getX() + Math.sin(bearing) * distance;
double genyY = getY() + Math.cos(bearing) * distance;
out.println("genyX:"+ Math.round(genyX));
out.println("genyY:"+ Math.round(genyY));
}
}
注意這兩個機器人我們都使用了AdvancedRobot的類,這可是高級機器人的說 明了。有關高級機器人大家可以查找Robocode API的說明,也可看看Sing Li的 "Rock 'em, sock 'em Robocode: Round 2".
距離探測
要得到目標坐標我們首先得知道我們和目標之間的距離。這裡的距離探測很 簡單,只要運用GenyTrack機器人ScannedRobotEvent事件中的 getDistance()方 法我們就可得到Geny機器人和你之間的距離差了。只是要注意一點,由於機器人 存在著寬和高,可分別用Robocode API 中的getWidth()和getHeigth()方法得到 。而兩個機器人的距離是以雙方的中心點為終點。如圖所示,L才是它們的距離 ,A的距離是錯誤的。
圖2
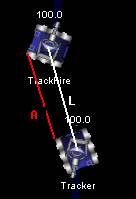
坐標探測
知道了對方的距離,知道了整個坐標系統。我們就來鎖定我們的目標Geny.我 們先來看看圖3所示:
圖3
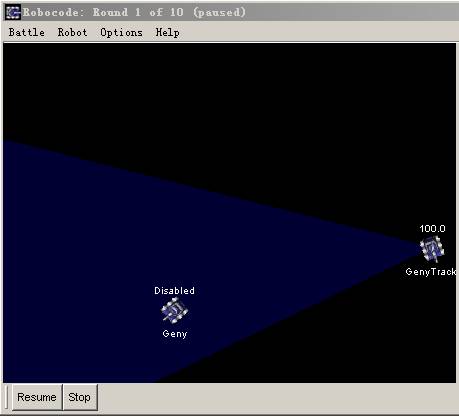
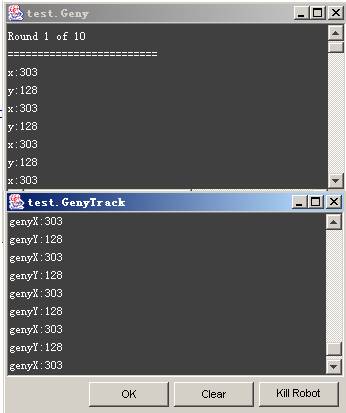
列表1:
Geny GenyTrack X:303 genyX:303 Y:128 genyY:128
列表1就是我們用”動靜機器人”測試法得出的數據。你將會驚喜若狂,不錯 ,我們成功的探測到了我們可憐的Geny的坐標。驚喜過後你就會不明白了:我們 是怎樣實現這一切的?為什麼代碼中使用到了非Robocode中的類庫Math,還似乎 用到了正余弦求解,還有弧度?不錯,這就是Robocode:處處都讓我們驚奇,處 處都讓我們學習新的知識。如果你對中學時代的數學三角幾何解法已經陌生,沒 關系,你將在我們本文最後的 三角函數基礎中將學習到這些。它將勾起你中學 時代的記憶。
現在讓我們來分析分析我們GenyTrack到底做了些什麼:
在 GenyTrack的ScanndeRobotEvent事件中我們首先得到Geny的絕對角度 bearing,也即相對屏幕的角度。並從 ScannedRobotEvent掃描事件中得到的大 量信息分析中提煉出Geny和GenyTrack的距離為distance。有了Geny的角度, 有 了Geny的距離我們再根據三角學基礎(詳見文 三角函數基礎)就可求出Geny的 精確坐標了。
又由於Java類庫中的正弦函數sin余弦函數cos是以弧度制(詳見文 三角函數 基礎)為角度的參數。所以我們利用了Math.toRadians方法把Geny的絕對角度轉 化為弧度。見列表2
列表2:
double bearing = (getHeading() + e.getBearing ()) % 360;
double distance = e.getDistance();
bearing = Math.toRadians(bearing);
double genyX = getX() + Math.sin(bearing) * distance;
double genyY = getY() + Math.cos(bearing) * distance;
out.println("genyX:"+ Math.round(genyX));
out.println("genyY:"+ Math.round(genyY));
注意三角函數的基礎中:對邊長=sina *斜邊長,側邊長=cosa*斜邊長,但 要記住Robocode中三角坐標系統中的sin和cos和我們數學中的三角坐標系統有一 定差別,也即上面的 sina和cosa要對換,對邊長=cosa*斜邊長。圖4畫出了Geny 和GenyTrack之間角度和距離的關系以及Robocode所采用的三角坐標系統。
圖4
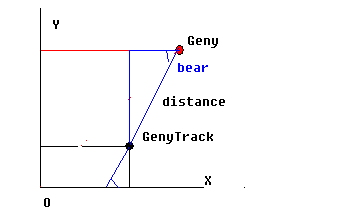
黑線條為GenyTrack的X,Y坐標,藍線條以Geny的距離distance和絕對角度 bear求得的X,Y坐標,兩者相加得到的就是Geny的X和Y坐標。
至於Math類庫的使用,我們就不詳細說明了。讀者也可從下面的IBM Java專 區鏈接中找到很多有關的知識,也可參考一些Java類庫書籍說明。當你設計高級 Robocode機器人時你會發現,Math類庫是你不可缺少的一部分知識。此處我們只 簡單的介紹正弦函數及余弦函數的使用。
Sin
public static double sin(double a)
Returns the trigonometric sine of an angle.
Parameters:
a - an angle, in radians.
Returns:
the sine of the argument
Sin函數返回三角的正弦函數,參數a是一個以double類型以弧度表示的角度 值,返回類型為double.
cos
public static double cos(double a)
Returns the trigonometric cosine of an angle.
Parameters:
a - an angle, in radians.
Returns:
the cosine of the argument
Cos函數返回三角的余弦函數,參數a是一個以double類型的弧度表示的角值, 返回類型為double.
有人會問為什麼不使用ScanndeRobot事件中的getRadarHeadingRadians()方 法直接得到弧度。哦,你來看看 Robocode中華聯盟iiley的一段說明:
public void onScannedRobot(ScannedRobotEvent event) {
enemyX=Math.sin(Util.standardMathDirRadians (getRadarHeadingRadians()))*event.getDistance();
enemyY=Math.cos(Util.standardMathDirRadians (getRadarHeadingRadians()))*event.getDistance();
}
看起來好像正確的,但是你實踐一下會發現他很不准確,為什麼呢?原因在 於getRadarHeadingRadians()函數,當你調用此函數的時候實際上雷達已經不在 剛剛掃描到敵人的那個角度了,他已經轉過了十幾度甚至更多。雷達默認轉動速 度是45度/robocode單位時間,實際上一般來說你用getRadarHeadingRadians() 得到的值總是45度的整數倍。(一些情況除外,比如說你用了turnRadarLeft (11)類似的語句以後)。
Robocode 也遵循數學應用中的基本法則用兩種方法來表示方向的角度:角度 制和弧度制,本文的代碼及以前文章中的代碼我們一直用的是角度制。另外一種 方法就是利用 ScannedRobotEvent.getBearingRadians() +robot.getHeadingRadians()得到敵人以弧度表示的方向,這個方法在本文章中 沒有說明了,有興趣的朋友可以自己試試用Java.util 類庫來實現. 也可參考文 檔 "精確計算敵人的坐標"。大家也可比較兩種方法各自特點,這將是個很有意 思的過程。
移動鎖定
當然,即使是最簡單的機器人也不會坐在那一動不動等著你來消滅。它會躲 避你的進攻以及掃描,當你向它原來坐標處開火,說不定它已經跑得老遠了,當 然這一切都不是我們所希望看到的。我們的目的是要消滅它:不管他是移動或靜 止的。下面我們就結合方向系統與坐標系統,來鎖定我們移動的目標。創造一個 我們自己的高級掃描機器人。建議你在此處下載源代碼( resource)並看看演示 效果再回到我們的文章中來。顯示如圖5:
圖5
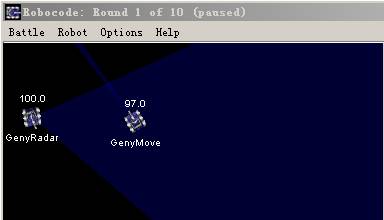
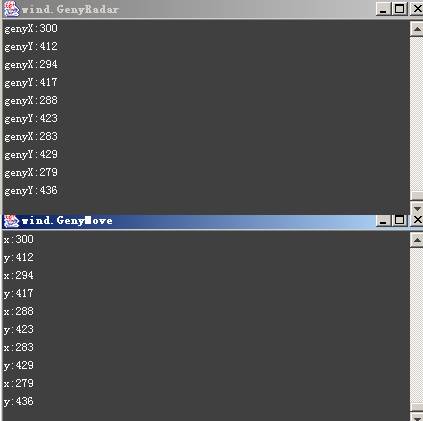
對比一下上面的數據,不管目標GenyMove在哪GenyRadar都能得到它精確的坐 標。是不是有一種成就感!是的,敵人已經完全在我們的掌握之中。即使它在移 動中也無法擺脫我們雷達的掃描控制。這裡只是很簡單舉了一些例子,GenyMove 在每一個時間周期(有關時間周期的說明見的 Rock 'em, sock 'em Robocode: Round2)移動自己的位置並打印出移動後的坐標,而GenyRadar掃描系統不停的 掃描目標,並一直追蹤,同時打印出掃描到的GenyMove方位。關鍵部分在我們的 ScannedRobotEvent事件如列表3
列表3:
public void onScannedRobot( ScannedRobotEvent e )
{
double heading = e.getBearing() +getHeading();
double distance = e.getDistance(); //求得距離
double ager_bearing = Math.toRadians(heading % 360); //角度轉為弧度
double genyX = getX() + Math.sin(ager_bearing) * distance;
double genyY = getY() + Math.cos(ager_bearing) * distance;
out.println("genyX:"+ Math.round(genyX));
out.println("genyY:"+ Math.round(genyY));
if( heading >= 360 )
heading = heading - 360;
if( heading < 0 )
heading = heading +360;
double bearing = getRadarHeading() - heading;
double radar_degree;
boolean radar_direction;
if( 0 <= bearing && bearing <= 180 )
{
radar_direction = LEFT;
}
else if( bearing <= -180 )
{
radar_direction = LEFT;
bearing = ( 360 + bearing );
}
else if( bearing < 0 )
{
radar_direction = RIGHT;
bearing =( -bearing );
}
else
{
radar_direction = RIGHT;
bearing = (360 - bearing);
}
radar_degree = bearing * 1.3 ; //加大每一時間周期 (tick)的掃描范圍
if( radar_direction == RIGHT )
{
setTurnRadarRight( radar_degree );
execute();
}
else
{
setTurnRadarLeft( radar_degree );
execute();
}
我們在代碼中首先求得GenyMove的絕對角度,然後用掃描時雷達的絕對角度 減去目標GenyMove的角度求得兩者的角度差也即我們雷達要旋轉的角度。最後利 用一個小技巧radar_degree = bearing * 1.3 使雷達在目標的范圍左右擺動以 擴大雷達掃描區域.這樣不管目標往哪邊移動都在自己的雷達掃描區內。
在此沒有進行很詳細的講解了,我想憑你學到的方向及坐標知識很快能明白 個中原理並設計出自己的高級掃描機器人來。聰明的你可能會高興的想,哈,我 的炮管用相同的辦法鎖定目標,這樣敵人不就沒辦法跑了,被我追著打。答案是 錯誤的,雷達的掃描是條長線能直接定位到目標上,它到目標的時間差幾乎為零 ,並且雷達的掃描范圍比炮管大且精確。而炮管每時間周期只有20度,它定位目 標是依靠著子彈,只有子彈打中了目標,才能說炮管的計算坐標是精確的。但是 由於子彈到達目標位置時需要一定的時間差,子彈本身又有速度值(20-3*power ),所以要想炮管鎖定目標並讓子彈擊中目標,我們還得經過精確的計算,並要 預測目標可能的行動:是直線前進,還是做圓周運動,還是隨機運動等等。這些 都是我們要充分考慮的因素。是不是很有挑戰性!這一切都在Robocode的世界中 等待著您的創造!
三角函數基礎
下面我們只是很簡單的介紹了一下與Robocode相關的三角函數知識,要想了 解詳細的,大家可從家中高中代數與幾何書中得到這一切。
1.角的概念
在平面內,角可以看作一條射線繞著它的端點旋轉而成的圖形。如圖,一條 射線由原來的位置OA,繞著它的端點O按逆時方向旋轉到另一位置OB,就形成角 a.旋轉開始時的射線OA叫做角a的始邊,旋轉終止時的射線OB叫做角a的終邊,射 線的端點O叫做角a的頂點。習慣上,我們把按逆時針方向旋轉而成的角叫做正角 ;按順時針方向旋轉而成的角叫做負角.所有與a終邊相同的角包括a在內,可以 用式子表示:a+K*360度,對應到Robocode的方向系統中,只要我們以機器人的 heading方向做射線,延長到與屏幕交點處的角度就是我們機器人的heading角度 。
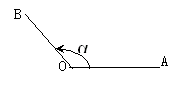
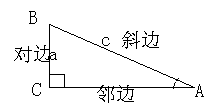
2.直角三角函數
在△ABC中,∠a為直角,我們把銳角A的對邊與斜邊的比叫做∠A的正弦,記 作sina;銳角a的鄰邊與斜邊的比叫做∠a的余弦,記作cosa,即
sina=對邊BC/斜邊AB
cosa=鄰邊AC/斜邊AB
3.單位圓和三角函數線
半徑為1的圓叫做單位圓。設單位圓的圓心與坐標原點重合,則單位圓與x軸 的交點分為別為A(1,0)、A′(-1,0),與y軸的交點分別為B(0,1)、 B′(0,- 1)。設角a的頂點在圓心O,始點與x軸的正半軸重合,終邊與單位圓相交於點P, 過點P作PM垂直x軸於M,則由直角三角函數的定義可知:OM=cosa,MP=sina ,點P 的坐標為(cosa,sina),即P(cosa,sina)。其中cosa=OM*1,sina=MP*1。 Robocode中所有有關的坐標都可用這種方法求得。
4.弧度制
用度做單位來度量角的制度叫做角度制。數學和其他科學研究中常用另一種 度量角的制度―弧度制。以角的頂點為圓心,以任意長的半徑作圓把這個角所對 的弧長與半徑的比來衡量角的制度叫做弧度制.長度等於半徑的弧長叫1弧度。這 段弧所對的圓心角的大小也是1弧度。通常單位“弧度”省略不寫。例:弧長為 1.3325。單位就是弧度。由角度和弧度兩種單位之間的關系得到:2π弧度=360度 ,2/3π弧度=270度,π弧度=180度,1/2π弧度=90 度,並可推出1弧度 = 360度/2 π = 57°即 1弧度=角度*180/Math.PI.
一般規定:正角的弧度數為正數,負角的弧度數為負數,零角的弧度數為零 。這樣角的集合與實數集合的元素就建立起了“一一對應”的關系。
哦,終於完了。到此為止,我們學習了Robocode基本原理中的方向系統和坐 標系統,當你對這兩個概念有一定的了解,你就可以創建自己的機器人,在戰爭 的洗禮中不斷完善自己的機器人,並適當的在你的機器人加入一些經典的戰斗策 略。它將越來越完美。不過不要忘了,一定要加入機器人的智能學習能力,只有 具有超強學習能力的機器人才能無敵於天下,在下一篇我們將會看到一個高智能 的機器人。