J2ME是標准版java(J2SE)面向手機、PDA等各類移動和嵌入式設備的縮減版本,是一種獲得眾多廠商的支持和廣泛使用的移動設備開發平台。圖一展示了J2ME技術的體系結構。它分為三層:虛擬機層,配置層,和簡表層。 配置層(Configuration)通過對功能的描述,把千差萬別的嵌入式設備進行了功能的說明和分類。它把運算功能有限、內存較小、電力有限的設備,定義在CLDC(有限連接設備配置)規范中,這類設備有PDA 、手機等;把運算能力相對較佳、內存相對較大、電力供應比較充足的設備,定義在CDC(連接設備配置)規范之中,這類設備有電冰箱、機頂盒、車載計算設備等。
虛擬機層(Virtual Machine)基於宿主操作系統,按照某一種配置,實現了Java虛擬機。CDC配置對應的虛擬機叫CVM,CLDC對應的虛擬機叫做KVM。
簡表層(Profile)建立在配置層之上,提供了面向用戶的更高層次的功能,如用戶接口,網絡,數據存儲等。基礎規范(Foundation Profile)和個人規范(Personal Profile)是CDC之上的兩個重要的規范,移動信息設備規范(MIDP)和PDA規范(PDAP)是CLDC之上的兩個重要的規范。當前,無線應用程序的開發主要是在MIDP之上進行的。
配置層和簡表層共同構成了J2ME的運行環境。如CLDC/MIDP架構構築了手機應用程序的開發和運行環境。本文所實現的圖像旋轉算法便是基於這種架構的。
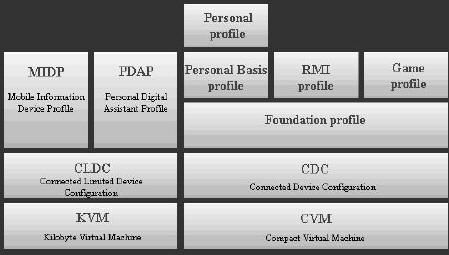
圖一 J2ME 體系結構 需要注意的是,這些規范也是在不斷發展的。如早期很多的設備的計算能力非常有限,CLDC1.0就只支持整型數值。後來數隨著設備運算能力的提高,CLDC1.0發展到CLDC1.1,就加如了對浮點運算的支持。對MIDP規范也一樣,從1.0發展到2.0,它通過擴充類和接口的功能,加強了對游戲開發的支持,增加了圖像處理功能(旋轉要用到),增強了對網絡功能的支持,如串口、套接字、https等。
2D旋轉的數據基礎
考慮笛卡兒直角坐標系中單個點旋轉的情況。如圖二示,這裡點P(x,y)到原點O繞O點逆時針旋轉角度θ後到點P′(x′,y′)。由三角函數的幾何意義,有x = r*cos α ,y = r*si n α和x′ = r*cos(α +θ) , y′ = r*sin(α + θ),推出:
x′ = x * cos θ – y * sin θ
y′ = y * cos θ + x * sin θ
當把旋轉點一般化為Q(x0,y0),得到:
x′ = x0 + (x - x0) cos θ - (y - y0) sin θ
y′ = y0 + (y - y0) cos θ + (x - x0) sin θ
在開發時,我們使用設備坐標系,它以屏幕的左上角為坐標原點,y軸方向向下。此時,我們不妨視θ為饒旋轉點順時針旋轉的角度,這樣,上面的公式依然成立。
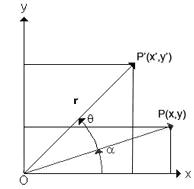
圖二 2D點的旋轉 一般圖像的旋轉算法
1、算法思想 為實現整個圖像的旋轉,我們首先獲取源圖像每個點的像素值。然後根據旋轉點和角度的大小計算出新圖像的大小。再逐點計算源圖像中每個點經旋轉後在新圖像中對應點的坐標,並把相應的像素值賦給它。
在圖三中,陰影部分為源圖像,O為旋轉點,P、Q分別為旋轉前後圖像左上角的點,cx,cy為O相對於源圖像左上角P點的坐標值。
這裡我們以O為圓心,以O距圖像4個頂點的距離的最大值作為半徑dr畫圓,這樣圖像無論以任何角度旋轉都不會超出這個圓的范圍。於是,我們就以該圓為畫布繪制旋轉所得新圖像。由於實際中圖像是用矩形表示的,於是我們生成和圓的外切正方形(圖中虛線部分)等大小的新圖像。
對源圖像中任一點(i,j),根據上面的公式,不難計算出旋轉θ度在新圖像中的位置,即相對於Q點的位置(destX , destY):
destX = dr + (i - cx) *cos(radian) - (j - cy)*sin(radian);
destY = dr + (j - cy) *cos(radian) + (i - cx)*sin(radian);
計算出這個位置後,把該點的像素值賦值到這個位置,如此對每個點進行這種變換,即可實現整個圖像的旋轉。
旋轉後的圖像較大,在實際繪制時需要做位置調整,不難看出,Q點相對於P點的偏移量為(cx-dr , cy-dr)。即假設源圖像的屏幕位置為(a , b),則旋轉後的圖像位置應該為( (a + cx – dr) , (b + cy – dr) )。
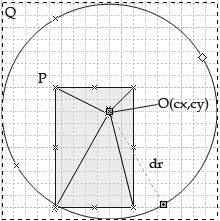
圖三 旋轉算法示意圖 2、在J2ME中的算法實現
我們將上面的思想具體化,得到算法的流程圖(見圖四示)
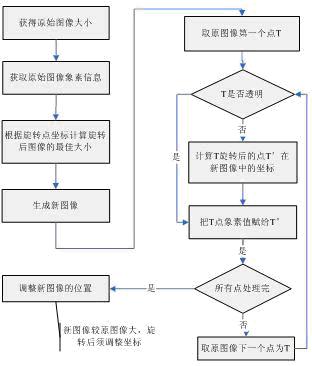
圖四 算法流程圖 在MIDP2.0中,Image類提供了兩個方法:getRGB()和createRGBImage(),分別完成獲取圖像象素信息和通過像素數組創建圖像的功能。借助於這兩個方法,結合上面的流程圖,我們得到實現圖像旋轉算法的代碼,如下面所示。 /**
*@param imgSource 源圖像
*@param cx 旋轉點相對於源圖像坐上角橫坐標
*@param cy 旋轉點相對於源圖像坐上角縱坐標
*@param theta 圖像逆時針旋轉的角度
*@param dd 含2個元素的整形數組,存放新圖像相對源圖像沿x軸和y軸的位置偏移量
*@return 旋轉後的圖像
**/
public Image rotate(Image imgSource, int cx, int cy, double theta, int[] dd) {
if (Math.abs(theta % 360) < 0.1) return imgSource; //角度很小時直接返回
int w1 = imgSource.getWidth(); //原始圖像的高度和寬度
int h1 = imgSource.getHeight();
int[] srcMap = new int[w1 * h1];
imgSource.getRGB(srcMap, 0, w1, 0, 0, w1, h1); //獲取原始圖像的像素信息
int dx = cx > w1 / 2 ? cx : w1 - cx; //計算旋轉半徑
int dy = cy > h1 / 2 ? cy : h1 - cy;
double dr = Math.sqrt(dx * dx + dy * dy);
int wh2 = (int) (2 * dr + 1); //旋轉後新圖像為正方形,其邊長+1是為了防止數組越界
int[] destMap = new int[wh2 * wh2]; //存放新圖像象素的數組
double destX, destY;
double radian = theta * Math.PI / 180; //計算角度計算對應的弧度值
for (int i = 0; i < w1; i++) {
for (int j = 0; j < h1; j++) {
if (srcMap[j * w1 + i] >> 24 != 0) { //對非透明點才進行處理
// 得到當前點經旋轉後相對於新圖像左上角的坐標
destX = dr + (i - cx) * Math.cos(radian) + (j - cy)* Math.sin(radian);
destY = dr + (j - cy) * Math.cos(radian) - (i - cx)* Math.sin(radian);
//從源圖像中往新圖像中填充像素
destMap[(int) destY * wh2 + (int) destX] = srcMap[j * w1 + i];
}
}
}
dd[0] = cx-dr; //返回位置偏移分量
dd[1] = cy-dr;
return Image.createRGBImage(destMap, wh2, wh2, true); //返回旋轉後的圖像
}
3、旋轉失真問題 因為旋轉公式含有三角函數,所以求出的旋轉坐標取整後有可能插入到先前已插入的位置中,而沒有插入到它本應該插入的位置。例如:計算出旋轉坐標(3.1,4)取整後插入到(3,4)中;如果計算下個旋轉坐標為(3.4,4),取整後又被插入到(3,4)中,因此覆蓋了原來的像素點,而且(3.4,4)對應的像素點沒有辦法插入到它應該插入的位置,造成失真。
要解決這個問題,在不考慮犧牲額外資源的情況下,一般的方法是先將圖像放大若干倍,然後再進行旋轉,再等比例縮小。對於邊界可考慮馬賽克的處理方式或者用兩行重描補償誤差的辦法。
算法的應用與局限性
1、模擬浮點運算
上述算法是基於cldc1.1規范的,該規范提供了對浮點運算和三角函數運算的直接支持。為提高程序的通用性,我們希望算法能運行在cldc1.0設備上。
cldc1.0不支持任何非整形的數值,要實現三角函數的計算,我們可以考慮用已有的整型數來模擬浮點數:把一個整數分成兩個域,分別存放浮點的整數和小數部分,這並不難,但要模擬通用的數學函數,如正弦、余弦、二次方根、指數運算等就不那麼容易了,需要花費不少時間。由於一些現有的庫已經能夠很好地完成這些工作,一般情況下,我們可以直接拿來用。
這裡我們選用Onne Hommes編寫的MathFP庫,該庫提供了基於整形int和長整形long的不同精度的實現,有簡單、健壯、速度快的特點。看下面使用該庫的示例代碼:
int xFP = MathFP.toFP(“0.10”);
int yFP = MathFP.toFP(“0.2”);
int zFP = MathFP.mul(xFP , yFP);
System.out.println( MathFP.toString( zFP ) ); //0.02
前兩行構造了兩個定點數0.10和0.2,第三行計算他們的乘積,並根據這個值構造定點數zFP,最後一行把zFP的值輸出。
這些定點值xFP,yFP,zFP不是真正意義上的整型值,雖然它們用整型值來存儲數據。使用這些定點值時必須調用相應的MathFP方法。
別的可以選用的浮點運算庫有JMFP、FPLib、shiftFP等。
2、使用預置的三角函數表
三角函數的計算一般比較慢,為提高運行速度,我們可以對數值進行預計算,比如提前計算出360?以內角度的正弦和余弦值,把結果存儲在一個靜態數組中,如下面代碼。
static int[] lookupCosFP = new int[360];
static int[] lookupSinFP = new int[360];
long radianFP ; //用於存放角度的弧度值
for(int i = 0; i<360; i++ ) {
//將角度轉化為弧度,使用MathFP庫
radianFP=MathFP.div(MathFP.mul(MathFP.toFP(i),MathFP.PI),MathFP.toFP(180)) ;
lookupCosFP = MathFP.cos(radianFP); //存入數組
lookupSinFP = MathFP.sin(radianFP);
}
這樣使用時,從數組中直接值就行了。事實上,根據三角函數的特點,我們只需預計算存儲0-90度的正弦函數值,便可以導出任意角度的正弦、余弦值。讀者可以編寫一個單獨的方法實現之。 由於移動設備的屏幕通常比較小,做高精度的三角函數運算的意義不大,所以一般采取近似模擬的辦法。(1)對有浮點支持/第三方庫支持的情況,不去存放每個角度的三角函數值,每隔5?存一個值。(2) 對於沒有浮點支持和第三方浮點庫支持的情況,在表中存放角度的三角函數值乘以某個較大數(如4096)取整後的值,在實際計算之後,再等比例縮小(除以4096)。這兩種方法在實際中都有不少應用。
3、Sprite中的圖像旋轉
Sprite,即精靈,是在游戲中代表角色的類,它管理所有的圖像幀來實現各種動畫效果,在游戲開發中有著廣泛的應用。如果需要表現動畫效果,那用Sprite是再合適不過的了。MIDP2.0中,提供了專門的這樣一個類,在構造時只需把圖像對象作為參數傳遞。Sprite類自身提供了圖像反射和成90度整數倍旋轉的功能。如果要實現任意角度旋轉,本質上跟上面的Image的旋轉沒有分別,只是在Sprite中內置了精靈的位置等信息,管理起來會更加方便高效。
讀者可以參考上面Image的實現,方便寫出基於Sprite的旋轉實現。需注意的是,Sprite一次只能取一幀圖像,因此需要首先把該幀從圖像集中提取出來。圖五展示了“淘金者”游戲中,精靈類“鉤子”的逆時針方向0到60?的旋轉效果圖。

圖五 鉤子的旋轉效果 4、局限性
(1)該算法的使用過程中生成了較大的圖像,比較適合於圖像繞固定點連續旋轉情況。如果實際中圖像只需做一次旋轉,或旋轉點經常變換,這種方法會產生較大的無效區域,增加處理的負擔,此時,旋轉後圖像的大小最好根據旋轉點和角度做最優化計算。
(2)算法需要獲得圖像的象素信息,這在midp2.0才給予支持,如果要在midp1.0的機器上實現圖像旋轉,須借助於設備廠商專用開發包,如Nokia開發包就提供了DirectUtils類實現類似上面createRGBImage()的功能。當然這只能在相應設備上才能用。
(3)算法要求設備支持Alpha通道,否則不能正常的表現效果。
(4)基於該方法的Sprite對象在做碰撞檢測時,須采用象素檢測的方法。
其余方案
1、預置圖像
預置圖像就是把所需要的各個角度的圖像預先存儲起來,然後按需直接調用的方法。這種方法不需要我們在程序中做像素級的操作,所以使用起來較簡單。缺點是當要存儲的圖像類別和角度很大時,會增加不少存儲開銷。
當所需要的各角度的圖像為偶數個且在0-360?范圍內均勻分布時,借助於MIDP2.0的Sprite類提供的順時針旋轉90?、180?、270?度的功能,我們可以在一定程度上降低這種開銷。比如在坦克大戰游戲中,假如一輛坦克需要一周范圍內均勻分布的12個不同的方向,則需預置12副圖像。借助於該方法,只需要提供三張圖片就夠了(見圖六),當它們分別旋轉90?、180?和270?後就得到了完整的12個方向,節省了3/4的存儲開銷。
圖六 預置圖像
2、使用TinyLine 2D
這是一個用於高性能圖形繪制的j2me開發包。它面向程序員,定義了一組緊湊的2d圖形對象集,擴展了j2me在移動設備上的圖形表現能力。它提供了基於CLDC 1.0 純Java語言的實現,很小巧,整個庫不足35k,能夠很方便地集成到應用程序當中去。需要說明的是,該庫不但支持圖形,對一般意義上的光柵圖像也支持,通過它也能實現旋轉等的操作。
結論
J2ME作為移動信息設備上的開發應用程序的開放平台,獲得了眾多廠商的支持,和越來越廣泛的使用。本文從數學的基礎出發,提出了實現圖像按任意角度旋轉的一種方案並給出了基於J2ME/MIDP平台的實現,給出了局限性分析,最後引出了實現圖像旋轉的另外兩種參考性方法。其實方法並沒有好劣之分,只有適合不適合之說,在實際應用中,我們應根據具體的需求,選擇最合適的方案。希望本文能給讀者在J2ME開發中需要用到圖像旋轉的功能時提供有益的參考