程式師世界 >> 編程語言 >> JAVA編程 >> 關於JAVA >> 詳解java數據結構與算法之雙鏈表設計與實現

詳解java數據結構與算法之雙鏈表設計與實現

編輯：關於JAVA

在單鏈表分析中，我們可以知道每個結點只有一個指向後繼結點的next域，倘若此時已知當前結點p，需要查找其前驅結點，那麼就必須從head頭指針遍歷至p的前驅結點，操作的效率很低，因此如果p有一個指向前驅結點的next域，那效率就高多了，對於這種一個結點中分別包含了前驅結點域pre和後繼結點域next的鏈表，稱之為雙鏈表。本篇我們將從以下結點來分析雙鏈表

雙鏈表的設計與實現

雙鏈表的主要優點是對於任意給的結點，都可以很輕易的獲取其前驅結點或者後繼結點，而主要缺點是每個結點需要添加額外的next域，因此需要更多的空間開銷，同時結點的插入與刪除操作也將更加耗時，因為需要更多的指針指向操作。雙鏈表的結構圖如下：

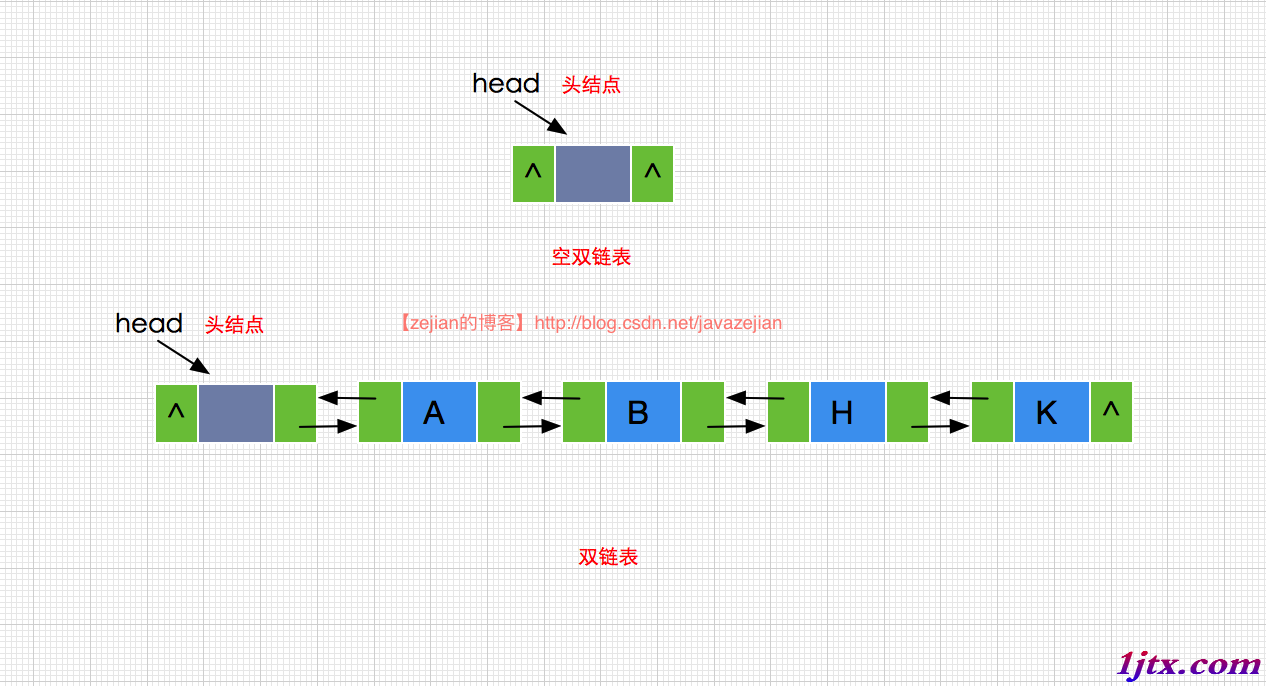
創建HeadDoubleILinkedList類並實現IlinekedList接口(和上篇博文的接口一樣)

/**
 * Created by zejian on 2016/10/23.
 * 雙鏈表的實現,帶頭結點(不帶數據)的雙鏈表,為了更高的效率該類包含指向尾部的指針tail
 */
public class HeadDoubleILinkedList<T> implements ILinkedList<T> {

  protected DNode<T> head; //不帶數據的頭結點
  protected DNode<T> tail; //指向尾部的指針

  public HeadDoubleILinkedList(){
    //初始化頭結點
    this.head =this.tail= new DNode<>();     
  }
  //先省略其他代碼
  ........
}

結點類結構如下：

package com.zejian.structures.LinkedList.doubleLinked;

/**
 * Created by zejian on 2016/10/23.
 * 雙鏈表結點
 */
public class DNode<T> {

  public T data;
  public DNode<T> prev, next;//前繼指針和後繼指針
  public DNode(T data, DNode<T> prev, DNode<T> next)
  {
    this.data = data;
    this.prev = prev;
    this.next = next;
  }

  public DNode(T data)
  {
    this(data, null, null);
  }

  public DNode()
  {
    this(null, null, null);
  }

  public String toString()
  {
    return this.data.toString();
  }
}

通過上篇的分析，我們對鏈表的插入、刪除、查找、替換等操作也比較熟悉了，因此針對雙鏈表的實現，主要分析其插入、刪除、查找、替換等方法，其他沒有分析的看實現源碼即可（最後會給出雙鏈表的實現代碼）

雙鏈表的插入操作分析與實現

我們先來看看雙鏈表的插入，雖然有不帶數據的頭結點，但是由於是雙向鏈表，所以在插入雙鏈表時需分兩種情況，一種是在插入空雙鏈表和尾部插入，另一種是雙鏈表的中間插入，如下圖在空雙鏈表插入值x：

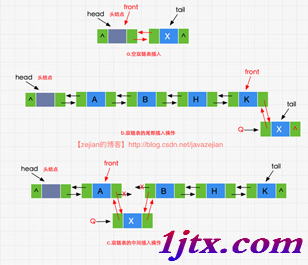
從圖可以看出（a）和（b）屬於同種情況，需要注意front.next != null的情況，否則就會拋空指針，而（c）的情況屬於中間插入無需無需理會front.next != null的條件，因為中間插入時無論如何其後繼結點時不會為null的，插入方法的實現代碼如下：

/**
 * 插入結點
 * @param index
 * @param data
 * @return
 */
@Override
public boolean add(int index, T data) {
  if(index<0||data==null)
    throw new NullPointerException("index < 0 || data == null");

    int j = 0;
    DNode<T> front = this.head;
    //查找要插入結點位置的前一個結點
    while (front.next != null && j < index) {
      j++;
      front = front.next;
    }

    //創建需要插入的結點,並讓其前繼指針指向front,後繼指針指向front.next
    DNode<T> q = new DNode<T>(data, front, front.next);

    //空雙鏈表插入和尾部插入，無需此操作
    if(front.next != null) {
      //更改front.next的前繼指針
      front.next.prev = q;
    }
    //更改front的後繼指針
    front.next = q;

    //在尾部插入時需要注意更新tail指向
    if(front==this.tail){
      this.tail=q;
    }
    return true;
}

雙鏈表的刪除操作分析與實現

雙鏈表的刪除操作與插入操作原理上是相似的，我們可以看出（a）（b）是屬於同種情況，需要防止 p.next.prev拋空指針的情況，而對於（c）情況則無需關系 p.next.prev的值，刪除的具體實現如下：

/**
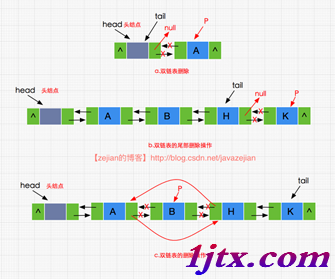
 * 根據下標刪除結點
 * 1.頭刪除
 * 2.中間刪除
 * 3.尾部刪除,更新tail指向
 * @param index 下標起始值為0
 * @return
 */
 @Override
 public T remove(int index) {

   int size=length();
   T temp=null;

   if(index<0||index>=size||isEmpty()){
     return temp;
   }

   DNode<T> p=this.head;
   int j=0;
   //頭刪除/尾刪除/中間刪除,查找需要刪除的結點(要刪除的當前結點因此i<=index)
   while (p!=null&&j<=index){
     p=p.next;
     j++;
   }
   //當雙鏈表只有一個結點時或尾部刪除時,無需此步
   if(p.next!=null){
     p.next.prev=p.prev;
   }
   p.prev.next=p.next;
   //如果是尾結點
   if (p==this.tail) {
     this.tail = p.prev;//更新未結點的指向
   }
   temp=p.data;

   return temp;
 }

雙鏈表的查值操作分析與實現

雙鏈表的查找值的操作與單鏈表並沒有什麼區別，只要找到需要查找的當前結點獲取其值即可，如下：

代碼實現如下：

@Override
public T get(int index) {
  if (index>=0)
  {
    int j=0;
    //注意起始結點為this.head.next
    //如果起始點為this.head時，j的判斷為j<=index，
    //因為需要尋找的是當前結點而不是前一個結點。
    DNode<T> pre=this.head.next;
    while (pre!=null && j<index)
    {
      j++;
      pre=pre.next;
    }
    if (pre!=null)
      return pre.data;
  }
  return null;
}

雙鏈表的替換值操作分析與實現

雙鏈表的替換值過程，需要先查找到需要替換的結點，這個過程跟獲取值的過程是一樣的，找到結點後直接替換值並返回舊值即可。比較簡單直接上代碼：

@Override
public T set(int index, T data) {
  T old=null;
  if (index>0&&data!=null){
    int j=0;
    DNode<T> pre =this.head.next;
    //查找需要替換的位置
    while (pre!=null&&j<index){
      j++;
      pre=pre.next;
    }
    if (pre!=null){
      old=pre.data;
      //替換數據
      pre.data=data;
    }
  }
  return old;
}

ok~，到此雙鏈表的主要操作實現已分析完，下面給出雙鏈表的實現源碼：

package com.zejian.structures.LinkedList.doubleLinked;

import com.zejian.structures.LinkedList.ILinkedList;

/**
* Created by zejian on 2016/10/23.
* 雙鏈表的實現,帶頭結點(不帶數據)的雙鏈表,為了更高的效率該類包含指向尾部的指針tail
*/
public class HeadDoubleILinkedList<T> implements ILinkedList<T> {

 protected DNode<T> head; //不帶數據的頭結點
 protected DNode<T> tail; //指向尾部的指針

 public HeadDoubleILinkedList(){
   this.head =this.tail= new DNode<>();     //初始化頭結點
 }


 /**
 * 傳入一個數組,轉換成鏈表
 * @param array
 */
 public HeadDoubleILinkedList(T[] array)
 {
   this();
   if (array!=null && array.length>0)
   {
     this.head.next = new DNode<T>(array[0]);
     tail =this.head.next;
     tail.prev=this.head;
     int i=1;
     while (i<array.length)
     {
       tail.next=new DNode<T>(array[i++]);
       tail.next.prev=tail;
       tail = tail.next;
     }
   }
 }

 @Override
 public boolean isEmpty() {
   return head.next==null;
 }


 @Override
 public int length() {
   int length=0;
   DNode<T> pre=head.next;
   while (pre!=null){
     length++;
     pre=pre.next;
   }
   return length;
 }


 @Override
 public T get(int index) {
   if (index>=0)
   {
     int j=0;
     DNode<T> pre=this.head.next;
     while (pre!=null && j<index)
     {
       j++;
       pre=pre.next;
     }
     if (pre!=null)
       return pre.data;
   }
   return null;
 }


 @Override
 public T set(int index, T data) {
   T old=null;
   if (index>0&&data!=null){
     int j=0;
     DNode<T> pre =this.head.next;
     //查找需要替換的位置
     while (pre!=null&&j<index){
       j++;
       pre=pre.next;
     }
     if (pre!=null){
       old=pre.data;
       //替換數據
       pre.data=data;
     }
   }
   return old;
 }

 /**
 * 插入結點
 * @param index
 * @param data
 * @return
 */
 @Override
 public boolean add(int index, T data) {
   if(index<0||data==null)
     throw new NullPointerException("index < 0 || data == null");

     int j = 0;
     DNode<T> front = this.head;
     //查找要插入結點位置的前一個結點
     while (front.next != null && j < index) {
       j++;
       front = front.next;
     }

     //創建需要插入的結點,並讓其前繼指針指向front,後繼指針指向front.next
     DNode<T> q = new DNode<T>(data, front, front.next);

     //空雙鏈表插入,需要確保front.next不為空
     if(front.next != null) {
       //更改front.next的前繼指針
       front.next.prev = q;
     }
     //更改front的後繼指針
     front.next = q;

     //在尾部插入時需要注意更新tail指向
     if(front==this.tail){
       this.tail=q;
     }

     return true;
 }

 /**
 * 尾部添加
 * @param data
 * @return
 */
 @Override
 public boolean add(T data) {
   if (data==null)
     return false;
   //創建新結點,並把其前繼指針指向tail
   DNode<T> q = new DNode<T>(data, tail, null);
   tail.next=q;
   //更新尾部結點
   this.tail=q;
   return true;
 }

 /**
 * 根據下標刪除結點
 * 1.頭刪除
 * 2.中間刪除
 * 3.尾部刪除,更新tail指向
 * @param index 下標起始值為0
 * @return
 */
 @Override
 public T remove(int index) {

   int size=length();
   T temp=null;

   if(index<0||index>=size||isEmpty()){
     return temp;
   }

   DNode<T> p=this.head;
   int j=0;
   //頭刪除/尾刪除/中間刪除,查找需要刪除的結點(要刪除的當前結點因此i<=index)
   while (p!=null&&j<=index){
     p=p.next;
     j++;
   }
   //當鏈表只要一個結點時,無需此步
   if(p.next!=null){
     p.next.prev=p.prev;
   }
   p.prev.next=p.next;
   //如果是尾結點
   if (p==this.tail) {
     this.tail = p.prev;//更新未結點的指向
   }
   temp=p.data;

   return temp;
 }

 /**
 * 根據data刪除結點,無需像單向鏈表那樣去存儲要刪除結點的前一個結點
 * 1.頭刪除
 * 2.中間刪除
 * 3.尾部刪除,更新tail指向
 * @param data
 * @return
 */
 @Override
 public boolean removeAll(T data) {

   boolean isRemove=false;

   if(data==null||isEmpty())
     return isRemove;

   //注意這裡的起點,如果起點為this.head,那麼情況區別如同前面的根據index的刪除實現
   DNode<T> p=this.head.next;

   //頭刪除/尾刪除/中間刪除(size>1),查找所有需要刪除的結點
   while (p!=null){

     if(data.equals(p.data)){
       if (p==this.tail){
         //如果是尾結點
         this.tail=p.prev;//更新未結點的指向
         p.prev=null;
         this.tail.next=null;
       }else {
         //如果是在中間刪除,更新前繼和後繼指針指向
         p.prev.next=p.next;
         p.next.prev=p.prev;
       }
       isRemove=true;
       p=p.next;//繼續查找
     }else {
       p=p.next;
     }

   }
   return isRemove;
 }

 /**
 * 清空鏈表
 */
 @Override
 public void clear() {
   this.head.next=null;
   this.tail=this.head;
 }


 @Override
 public boolean contains(T data) {

   if(data==null){
     return false;
   }

   DNode<T> p=this.head.next;
   while (p!=null){
     if (data.equals(p.data)){
       return true;
     }else {
       p=p.next;
     }
   }

   return false;
 }

 @Override
 public String toString() {
   String str="(";
   DNode<T> pre = this.head.next;
   while (pre!=null)
   {
     str += pre.data;
     pre = pre.next;
     if (pre!=null)
       str += ", ";
   }
   return str+")";
 }

 public static void main(String[] args){

   String[] letters={"A","B","C","D","Z","E","F"};
//    String[] letters={"A"};
   HeadDoubleILinkedList<String> list=new HeadDoubleILinkedList<>(letters);

   System.out.println("list.get(3)->"+list.get(3));
   System.out.println("list:"+list.toString());

   System.out.println("list.add(4,Y)—>"+list.add(0,"Y"));
   System.out.println("list:"+list.toString());
   System.out.println("list.add(Z)—>"+list.add("Z"));
   System.out.println("list:"+list.toString());


   System.out.println("list.contains(Z)->"+list.contains("Z"));
   System.out.println("list.set(4,P)-->"+list.set(4,"P"));
   System.out.println("list:"+list.toString());


   System.out.println("list.remove(6)-->"+list.remove(6));
//    System.out.println("list.remove(Z)->"+list.removeAll("Z"));
   System.out.println("list:"+list.toString());
 }
}

循環雙鏈表的設計與實現

如果雙鏈表的最後一個結點的next指針域指向頭結點，而頭結點的prev指針指向頭最後一個結點，則構成了雙鏈表（Circular Doubly LinkedList），其結構如下圖示：

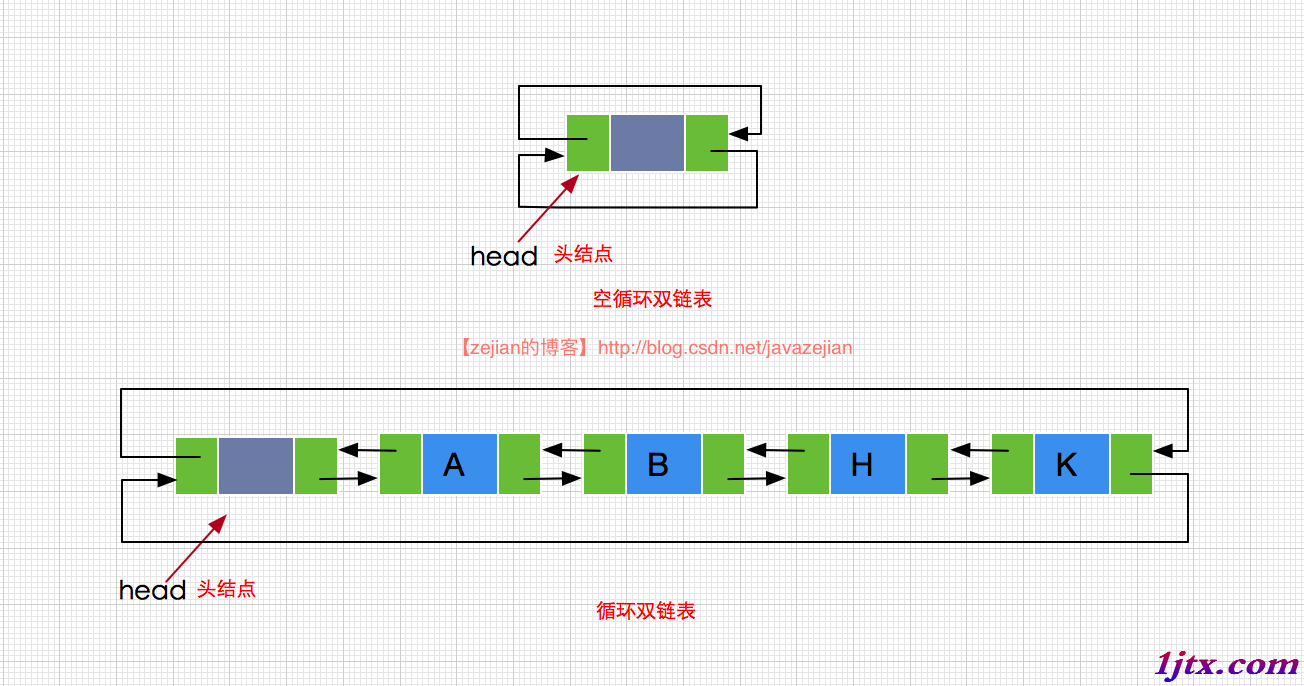
在循環雙鏈表中我們不再需要尾指向結點，因為整個鏈表已構成循環，在頭結點head的位置也可以輕松獲取到尾部結點的位置。對於循環雙鏈表的插入、刪除操作也無需區分位置操作的情況，這是由於循環雙鏈表的本身的特殊性，使p.next.pre永遠不可能為null，因此我們在插入和刪除時代碼實現相對簡單些。下面我們先分析一下循環雙鏈表的插入操作，圖示如下：

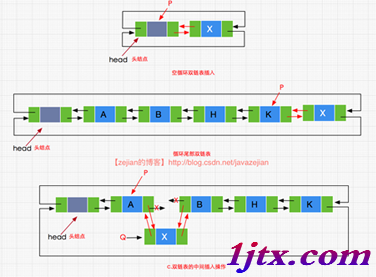
我們可以看出（a）（b）（c）三種情況都無需關系位置插入的區別，其代碼實現如下：

/**
 * 根據index插入
 * 循環鏈表中無論是prev還是next都不存在空的情況,因此添加時
 * 無論是頭部還是尾部還是中,都視為一種情況對待
 * @param index
 * @param data
 * @return
 */
@Override
public boolean add(int index, T data) {
  int size=length();
  if(data==null||index<0||index>=size)
    return false;

  int j=0;
  DNode<T> p=this.head;
  //尋找插入點的位置
  while (p.next!=head&&j<index){
    p=p.next;
    j++;
  }

  //創建新結點,如果index=3,那麼插入的位置就是第4個位置
  DNode<T> q=new DNode<>(data,p,p.next);
  p.next=q;
  p.next.prev=q;

  return true;
}

循環雙鏈表的刪除操作圖示如下：

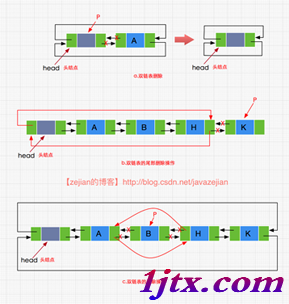
雙鏈表的刪除操作圖示

同樣地，從圖中我們也可以發現由於循環雙鏈表的特性，（a）（b）（c）三種情況都無需區分操作位置，其代碼實現如下：

@Override
public T remove(int index) {
  T old = null;
  int size=length();

  if (index<0||index>=size)
    return old;

  int j=0;
  DNode<T> p=this.head.next;

  while (p!=head && j<index)
  {
    j++;
    p = p.next;
  }

  if (p!=head)
  {
    old = p.data;
    p.prev.next = p.next;
    p.next.prev = p.prev;
  }
  return old;
}

至於循環雙鏈表的查找值、替換值等操作與雙鏈表並沒有多大的區別，但是需要特別注意的是在遍歷循環雙鏈表時，結束標志不再是尾部結點是否為空，而是尾結點的next指針是否指向頭結點head。好~，下面我們給出循環雙鏈表的實現代碼：

package com.zejian.structures.LinkedList.doubleLinked;

import com.zejian.structures.LinkedList.ILinkedList;

/**
* Created by zejian on 2016/10/24.
* 循環雙鏈表,帶空頭結點(不含數據),循環鏈表可以不需要尾部指針
*/
public class LoopHeadDILinkedList<T> implements ILinkedList<T> {

 protected DNode<T> head; //不帶數據的頭結點
//  protected DNode<T> tail; //指向尾部的指針

 public LoopHeadDILinkedList(){
   this.head = new DNode<>();//初始化頭結點
   this.head.next=head;
   this.head.prev=head;

 }

 

 /**
 * 傳入一個數組,轉換成鏈表
 * @param array
 */
 public LoopHeadDILinkedList(T[] array)
 {
   this();
   if (array!=null && array.length>0)
   {
     DNode<T> p= new DNode<>(array[0]);
     head.next=p;
     head.prev=p;
     p.prev=head;
     p.next=head;

     int i=1;
     while (i<array.length)
     {
       p.next=new DNode<>(array[i++],p,head);
       head.prev=p.next;
       p=p.next;
     }
   }
 }

 

 @Override
 public boolean isEmpty() {
   return this.head.next==head;//循環雙鏈表的後繼指針指向自己說明是空鏈表
 }

 @Override
 public int length() {

   int length=0;
   DNode<T> p=this.head.next;
   while (p!=this.head){
     length++;
     p=p.next;
   }
   return length;
 }

 @Override
 public T get(int index) {

   if (index>=0)
   {
     int j=0;
     DNode<T> p=this.head.next;
     while (p!=head && j<index)
     {
       j++;
       p=p.next;
     }
     if (p!=head)
       return p.data;
   }
   return null;
 }

 /**
 * 根據index修改data
 * @param index
 * @param data
 * @return 返回被替換的data
 */
 @Override
 public T set(int index, T data) {

   if (data==null){
     return null;
   }

   if(index>=0){
     int j=0;
     DNode<T> p=this.head.next;

     while (p!=head&&j<index){
       j++;
       p=p.next;
     }

     //如果不是頭結點
     if(p!=head){
       T old = p.data;
       p.data=data;

       return old;
     }
   }

   return null;
 }

 /**
 * 根據index添加
 * 循環鏈表中無論是prev還是next都不存在空的情況,因此添加時
 * 無論是頭部還是尾部還是中,都視為一種情況對待
 * @param index
 * @param data
 * @return
 */
 @Override
 public boolean add(int index, T data) {
   int size=length();
   if(data==null||index<0||index>=size)
     return false;

   int j=0;
   DNode<T> p=this.head;
   //尋找插入點的位置
   while (p.next!=head&&j<index){
     p=p.next;
     j++;
   }

   //創建新結點,如果index=3,那麼插入的位置就是第4個位置
   DNode<T> q=new DNode<>(data,p,p.next);
   p.next=q;
   p.next.prev=q;

   return true;
 }

 /**
 * 尾部添加
 * @param data
 * @return
 */
 @Override
 public boolean add(T data) {

   if(data==null)
     return false;
   //創建新結點,讓前繼指針指向head.pre,後繼指針指向head
   DNode<T> p=new DNode<>(data,head.prev,head);
   //更新tail後繼指針的指向
   this.head.prev.next=p;
   this.head.prev=p;

   return true;
 }

 @Override
 public T remove(int index) {
   T old = null;
   int size=length();

   if (index<0||index>=size)
     return old;

   int j=0;
   DNode<T> p=this.head.next;

   while (p!=head && j<index)
   {
     j++;
     p = p.next;
   }

   if (p!=head)
   {
     old = p.data;
     p.prev.next = p.next;
     p.next.prev = p.prev;
   }

   return old;
 }

 @Override
 public boolean removeAll(T data) {
   boolean isRemove=false;

   if(data==null){
     return isRemove;
   }

   DNode<T> p=this.head.next;
   while (p!=head){
     if(data.equals(p.data)){
       p.prev.next=p.next;
       p.next.prev=p.prev;
       isRemove=true;
     }
     p=p.next;
   }

   return isRemove;
 }

 @Override
 public void clear() {
   this.head.prev = head;
   this.head.next = head;
 }

 @Override
 public boolean contains(T data) {

   if (data==null){
    return false;
   }

   DNode<T> p=this.head.next;

   while (p!=head){
     if(data.equals(p.data)){
       return false;
     }

     p=p.next;
   }

   return false;
 }

 @Override
 public String toString()
 {
   String str="(";
   DNode<T> p = this.head.next;
   while (p!=head)
   {
     str += p.data.toString();
     p = p.next;
     if (p!=head)
       str += ", ";
   }
   return str+")";
 }
 public static void main(String[] args){

   String[] letters={"A","B","C","D","Z","E","F"};
   LoopHeadDILinkedList<String> list=new LoopHeadDILinkedList<>(letters);

   System.out.println("init list-->"+list.toString());

   System.out.println("list.get(3)->"+list.get(3));
   System.out.println("list:"+list.toString());

   System.out.println("list.add(4,Y)—>"+list.add(4,"Y"));
   System.out.println("list:"+list.toString());
   System.out.println("list.add(Z)—>"+list.add("Z"));
   System.out.println("list:"+list.toString());


   System.out.println("list.contains(Z)->"+list.contains("Z"));
   System.out.println("list.set(4,P)-->"+list.set(4,"P"));
   System.out.println("list:"+list.toString());


   System.out.println("list.remove(3)-->"+list.remove(3));
   System.out.println("list.remove(Z)->"+list.removeAll("Z"));
   System.out.println("list:"+list.toString());
 }
}

排序循環雙鏈表的實現

所謂的排序循環雙鏈表指的是在插入元素時，不再根據index標志，而是根據值的大小尋找插入位置，但是有個插入值data必須是T或者T的父類而且實現了Comoarable接口。排序循環雙鏈表的實現比較簡單，我們只需繼承前面的循環雙鏈表並重寫add方法即可，主要代碼實現如下：

package com.zejian.structures.LinkedList.doubleLinked;

/**
* Created by zejian on 2016/11/6.
* 升序排序鏈表，繼承LoopHeadDILinkedList
*/
public class SortLoopHeadDIlinkedList<T extends Comparable<? extends T>> extends LoopHeadDILinkedList<T> {
 /**
  * 順序插入
  * @param data
  * @return
  */
 @Override
 public boolean add(T data) {

   if(data==null||!(data instanceof Comparable))
     throw new NullPointerException("data can\'t be null or data instanceof Comparable must be true");

   Comparable cmp =data;//這裡需要轉一下類型,否則idea編輯器上檢驗不通過.

   //如果data值比最後一個結點大,那麼直接調用父類方法,在尾部添加.
   if(this.isEmpty() || cmp.compareTo(this.head.prev.data) > 0){
     return super.add(data);
   }

   DNode<T> p=this.head.next;
   //查找插入點
   while (p!=head&&cmp.compareTo(p.data)>0)
     p=p.next;

   DNode<T> q=new DNode<>(data,p.prev,p);
   p.prev.next=q;
   p.prev=q;

   return true;
 }

 public static void main(String[] args){
   SortLoopHeadDIlinkedList<Integer> list=new SortLoopHeadDIlinkedList<>();
   list.add(50);
   list.add(40);
   list.add(80);
   list.add(20);
   System.out.println("init list-->"+list.toString());
 }
}

雙鏈表的執行效率分析

其實上一篇已分析得差不多了，這裡再簡單說明一下，鏈表在插入和刪除元素時執行效率比較高，從插入操作來看，我們假設front指向的是雙向鏈表中的一個結點，此時插入front的後繼結點或者是前驅結點所消耗的時間為常數時間O(1),這點在插入front的前驅結點的效率比單鏈表有所改善，無需從頭結點開始遍歷，但是上述都是從已知雙向鏈表中front結點的情況下討論的。如果從實現代碼的操作上看，無論是插入還是刪除，都需要查找插入結點或刪除結點，而這個過程訪問結點所花費的時間的是O(n)，因此雙鏈表的插入或刪除操作或是查值操作，其時間復雜度都為O(n),至於為什麼說鏈表更適合插入刪除，這點上一篇我們已討論過，這裡就不重復了。最後給出一張關於鏈表、數組、動態數組的比較表：

傳遞參數鏈表動態數組索引 O(n) O(1) 在最前端插入或刪除 O(1) O(n) 在最末端插入 O(n) O(1),如果數組空間沒有被填滿;O(n),如果數組空間已填滿在最末端刪除 O(n) O(1) 在中間插入 O(n) O(n) 在中間刪除 O(n) O(n) 空間浪費 O(n) O(n)

異或高效存儲雙鏈表的設計原理概要

在上述分析的雙鏈表的實現中，都是需要一個指向後繼結點的正向指針和一個指向前驅結點的反向指針，出於此點的考慮，我們需要在構造一個結點類時需要一個數據域data、一個指向後繼結點的指針next以及一個指向前驅結點的指針prev。但為了設計更高效節省存儲空間，一種基於指針差運算存儲高效的雙向鏈表就誕生了。這種鏈表的每個結點仍然與單鏈表一樣僅使用一個指針域來設計雙向鏈表，新的雙向鏈表結點類結構如下：

package com.zejian.structures.LinkedList.XORLinked;

/**
 * Created by zejian on 2016/11/6.
 * 異或結點
 */
public class XORNode<T> {
  public T data;
  public XORNode<T> ptrdiff;//異或指針

  public XORNode() {
  }

  public XORNode(T data, XORNode<T> ptrdiff) {
    this.data = data;
    this.ptrdiff = ptrdiff;
  }
}

其中的ptrdiff字段存儲了後繼結點與前驅結點的地址差，指針的差通過異或運行（對異或不熟悉的可以看博主的另一篇文章：java運算符）來實現的，我們這裡使用⊕表示異或操作，則有如下計算：

pridiff=後繼結點的地址⊕前驅結點的地址

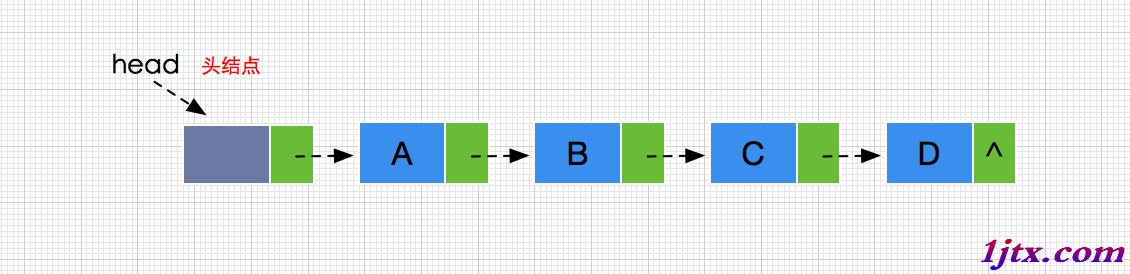
如上圖，我們采用異或差值來計算各個結點的位置：

A的next域為head⊕B B的next域為A⊕C C的next域為B⊕D D的next域為C⊕NULL

那麼為什麼可以這麼計算呢？我們先來了解一下異或的特性：

X⊕X=0 X⊕0=X X⊕Y=Y⊕X (X⊕Y)⊕Z=X⊕(Y⊕Z)

所以我們可以很容易利用上述的異或特性找到結點的對象，比如指向P想從結點C移動到結點B，已知C的ptrdiff值為B⊕D,那麼就需要將結點C的ptrdiff的值與結點D的地址執行異或運算，這時就可以得到B的地址了，計算過程如下：

(B ⊕ D) ⊕ D = B ⊕(D ⊕ D) = B ⊕ 0 =B

如果想從C結點移動到D結點，那麼此時的計算如下：

(B ⊕ D) ⊕ B = D ⊕(B ⊕ B) =B ⊕ 0 = D

因此在確實可以通過一個next的指針域來實現雙向鏈表的移動，而且這種存儲高效的雙向鏈表還可以節省空間開銷。實際上，存儲高效的雙鏈表介紹來自《數據結構與算法經典問題分析》一書，不過博主發現，這種存儲高效的鏈表，使用C語言比較容易實現，因為c語言可以通過指針(地址)獲取到對象直接操作，但在Java語言中，博主並沒有想到如何實現這種存儲高效的鏈表，至少目前還沒想到可行的方案，google了一把實現語言都是C，沒找到java的實現，不過博主想來想去都感覺這種存儲高效的鏈表不太適合java來實現（僅個人觀點），若有實現方案的還望留言告知，感謝呢。不過這樣算法設計思想方式還是蠻有不錯的。ok~，關於雙向鏈表，我們暫且聊到這裡。

以上就是本文的全部內容，希望對大家的學習有所幫助，也希望大家多多支持。