You are given a string, s, and a list of words, words, that are all of the same length. Find all starting indices of substring(s) in s that is a concatenation of each word in words exactly once and without any intervening characters.
For example, given:
s: "barfoothefoobarman"
words: ["foo", "bar"]
You should return the indices: [0,9].
(order does not matter).
簡單的翻譯:給定一個字符串s和一個字列表words,所有的字是相同長度的。找出所有s的字串中包含有words中所有元素的下標,並且順序無所謂。
對於每一次的移動判斷,判斷窗體內的字符串是否是有給定的字符串數組中的元素組成,這個是用map或者其他的數據結構來判斷的。因為是不用計較順序的,所以有可以簡化為判斷存在與否的問題。判斷存在與否則是通過累計判斷的,即每次從輸入串提取出wordsp[0].length長度的字串判斷其是否存在於words中,並且數目一定要相同,即words中有一個“abaad”,則窗口對應的串中也只能有一個”abaad”。
使用一個map保存words中的數據用來對比,一個新的map用來保存窗對應的數據,這樣通過比較兩個map中的數據就可以判斷是否匹配了。並且使用map結構可以減少取值的操作過程,當每次窗移動時,只需要從map中除去原窗口位置對應的第一個word即可,這樣新的串口對應的數據只需要添加一個word即可,可以減少words.length-1次的提取數據的操作。(代碼來自網上分享)

public class Solution {
/*
A time & space O(n) solution
Run a moving window for wordLen times.
Each time we keep a window of size windowLen (= wordLen * numWord), each step length is wordLen.
So each scan takes O(sLen / wordLen), totally takes O(sLen / wordLen * wordLen) = O(sLen) time.
One trick here is use count to record the number of exceeded occurrences of word in current window
*/
public static List<Integer> findSubstring(String s, String[] words) {
List<Integer> res = new ArrayList<>();
if(words == null || words.length == 0 || s.length() == 0) return res;
int wordLen = words[0].length();
int numWord = words.length;
int windowLen = wordLen * numWord;
int sLen = s.length();
HashMap<String, Integer> map = new HashMap<>();
for(String word : words) map.put(word, map.getOrDefault(word, 0) + 1);
for(int i = 0; i < wordLen; i++) { // Run wordLen scans
HashMap<String, Integer> curMap = new HashMap<>();
for(int j = i, count = 0, start = i; j + wordLen <= sLen; j += wordLen) { // Move window in step of wordLen
// count: number of exceeded occurences in current window
// start: start index of current window of size windowLen
if(start + windowLen > sLen) break;
String word = s.substring(j, j + wordLen);
if(!map.containsKey(word)) {
curMap.clear();
count = 0;
start = j + wordLen;
}
else {
if(j == start + windowLen) { // Remove previous word of current window
String preWord = s.substring(start, start + wordLen);
start += wordLen;
int val = curMap.get(preWord);
if(val == 1) curMap.remove(preWord);
else curMap.put(preWord, val - 1);
if(val - 1 >= map.get(preWord)) count--; // Reduce count of exceeded word
}
// Add new word
curMap.put(word, curMap.getOrDefault(word, 0) + 1);
if(curMap.get(word) > map.get(word)) count++; // More than expected, increase count
// Check if current window valid
if(count == 0 && start + windowLen == j + wordLen) {
res.add(start);
}
}
}
}
return res;
}
}
View Code
關於外層循環的存在,從我們的繪圖可以看到窗的出發點是0,但是有可能從1開始的窗對應的才是我們想要的,所以要加入外層循環遍歷所有的可能,之所以到words[0].length就結束是因為,當窗的開始為值為words[0].length的時候,可以發現它是第一次移動窗的結果,也就是重復了,所以就不用繼續執行了。想象一下即可。
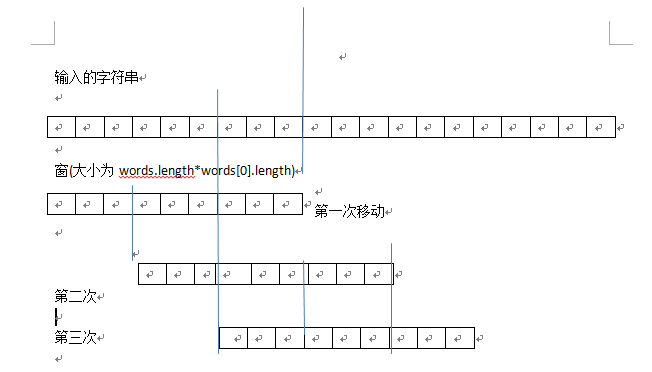
輸入的字符串
窗(大小為words.length*words[0].length)
第一次移動
第二次
第三次
對於每一次的移動判斷,判斷窗體內的字符串是否是有給定的字符串數組中的元素組成,這個是用map或者其他的數據結構來判斷的。因為是不用計較順序的,所以有可以簡化為判斷存在與否的問題。判斷存在與否則是通過累計判斷的,即每次從輸入串提取出wordsp[0].length長度的字串判斷其是否存在於words中,並且數目一定要相同,即words中有一個“abaad”,則窗口對應的串中也只能有一個”abaad”。
使用一個map保存words中的數據用來對比,一個新的map用來保存窗對應的數據,這樣通過比較兩個map中的數據就可以判斷是否匹配了。並且使用map結構可以減少取值的操作過程,當每次窗移動時,只需要從map中除去原窗口位置對應的第一個word即可,這樣新的串口對應的數據只需要添加一個word即可,可以減少words.length-1次的提取數據的操作。