前面幾節介紹了Java中的基本容器類,每個容器類背後都有一種數據結構,ArrayList是動態數組,LinkedList是鏈表,HashMap/HashSet是哈希表,TreeMap/TreeSet是紅黑樹,本節介紹另一種數據結構 - 堆。
引入堆
之前我們提到過堆,那裡,堆指的是內存中的區域,保存動態分配的對象,與棧相對應。這裡的堆是一種數據結構,與內存區域和分配無關。
堆是什麼結構呢?這個我們待會再細看。我們先來說明,堆有什麼用?為什麼要介紹它?
堆可以非常高效方便的解決很多問題,比如說:
堆還可以實現排序,稱之為堆排序,不過有比它更好的排序算法,所以,我們就不介紹其在排序中的應用了。
Java容器中有一個類PriorityQueue,就表示優先級隊列,它實現了堆,下節我們會詳細介紹。關於後面兩個問題,它們是如何使用堆高效解決的,我們會在接下來的幾節中用代碼實現並詳細解釋。
說了這麼多好處,堆到底是什麼呢?
堆的概念
完全二叉樹
堆首先是一顆二叉樹,但它是完全二叉樹。什麼是完全二叉樹呢?我們先來看另一個相似的概念,滿二叉樹。
滿二叉樹是指,除了最後一層外,每個節點都有兩個孩子,而最後一層都是葉子節點,都沒有孩子。比如,下圖兩個二叉樹都是滿二叉樹。
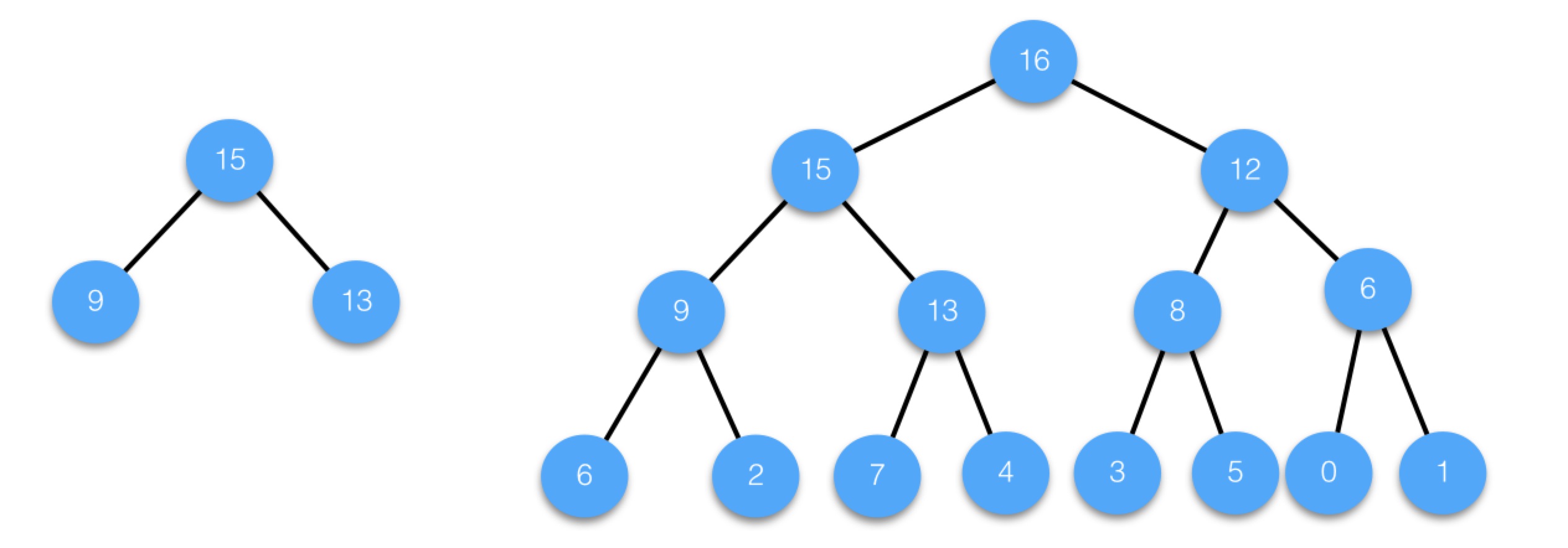
滿二叉樹一定是完全二叉樹,但完全二叉樹不要求最後一層是滿的,但如果不滿,則要求所有節點必須集中在最左邊,從左到右是連續的,中間不能有空的。比如說,下面幾個二叉樹都是完全二叉樹:
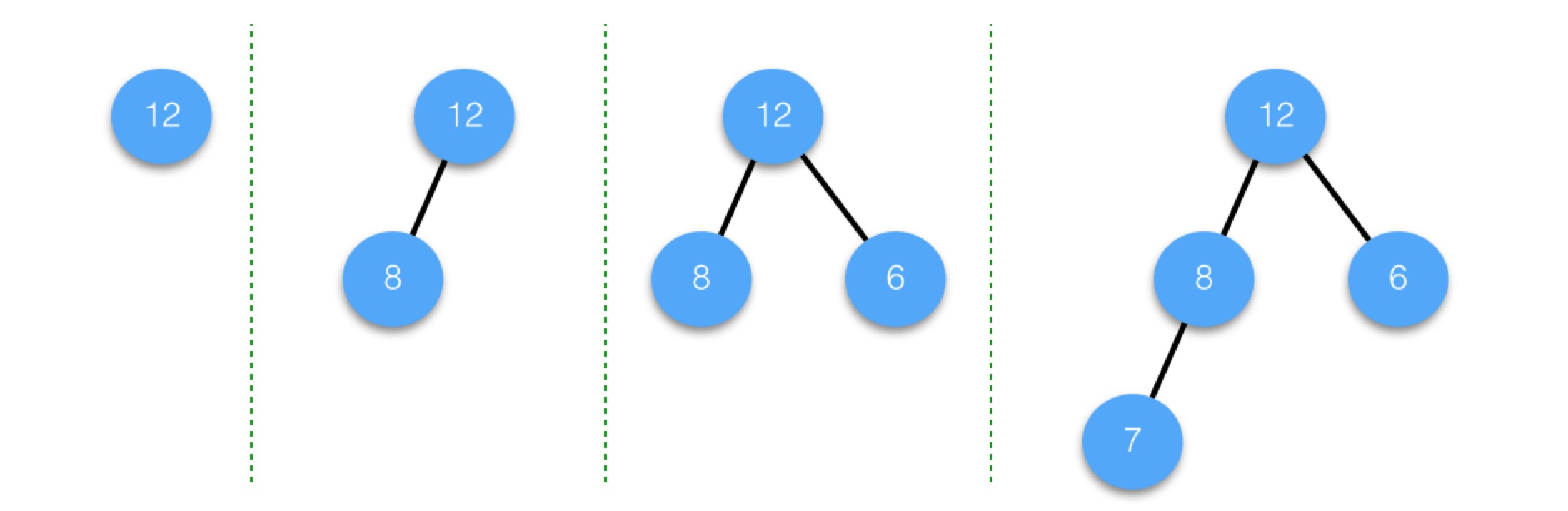
而下面的這幾個則都不是完全二叉樹:
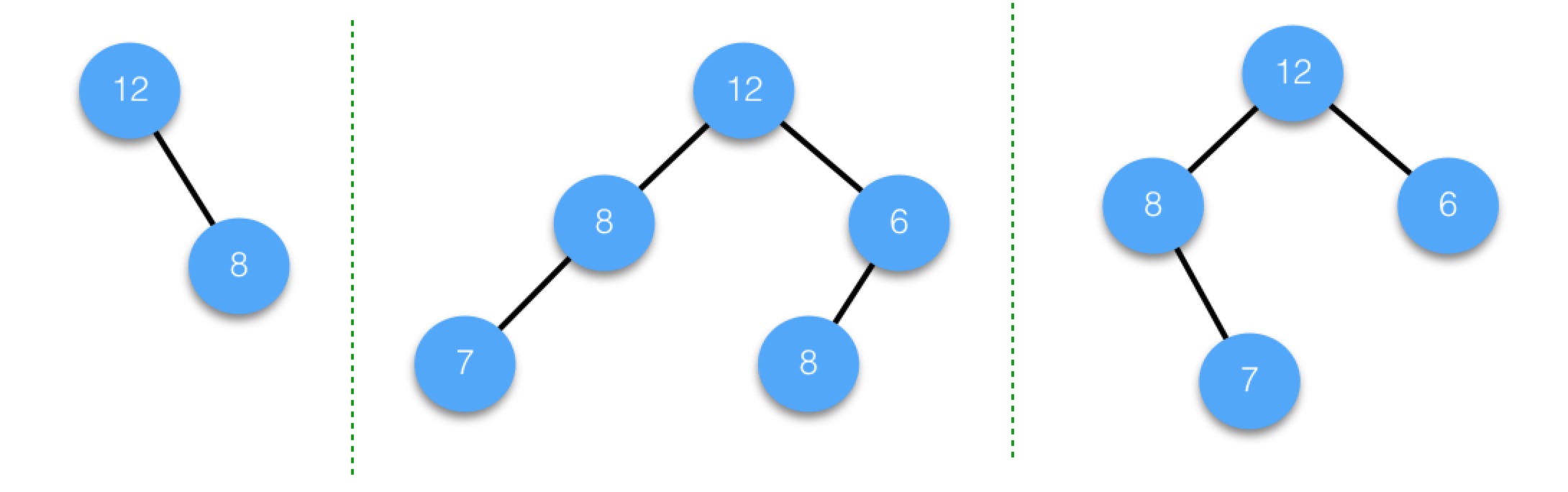
編號與數組存儲
在完全二叉樹中,可以給每個節點一個編號,編號從1開始連續遞增,從上到下,從左到右,如下圖所示:
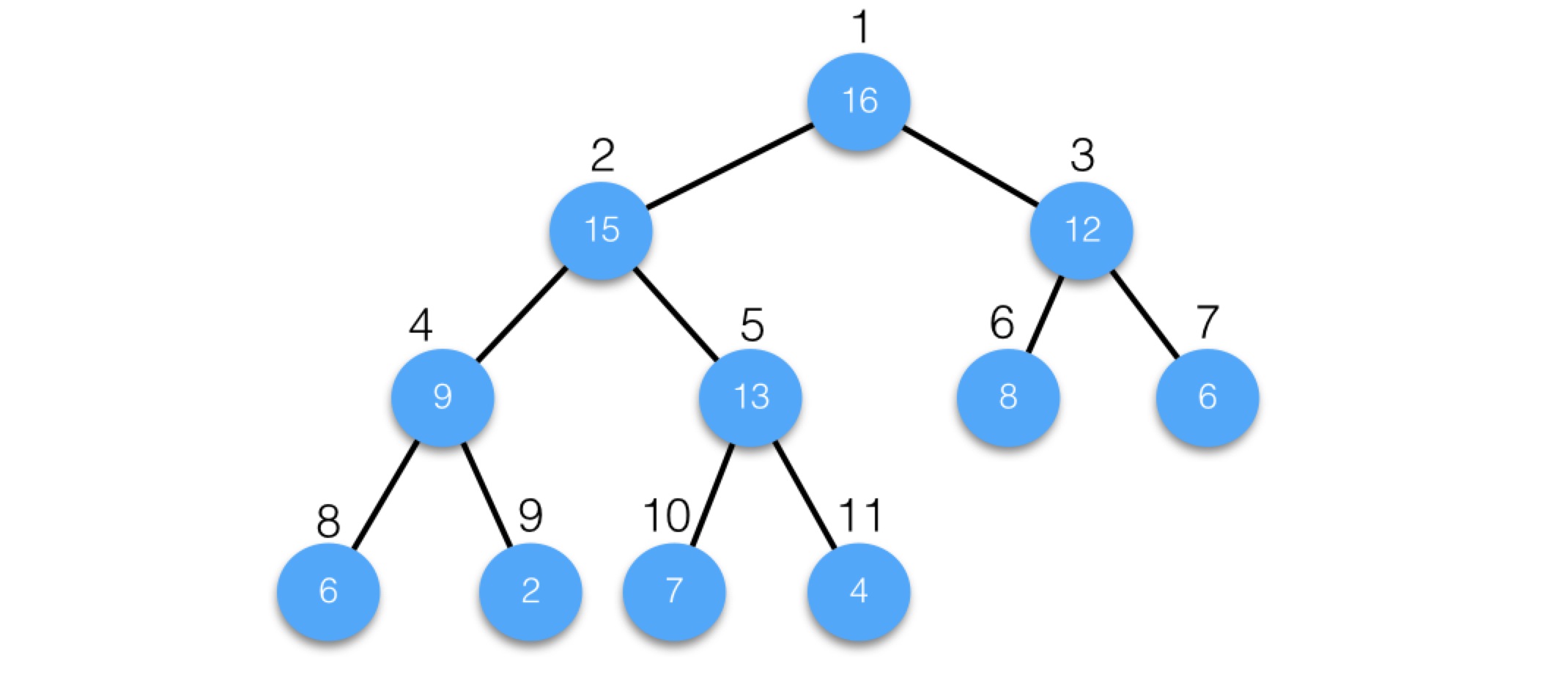
完全二叉樹有一個重要的特點,給定任意一個節點,可以根據其編號直接快速計算出其父節點和孩子節點編號,如果編號為i,則父節點編號即為i/2,左孩子編號即為2*i,右孩子編號即為2*i+1。比如,對於5號節點,父節點為5/2即2,左孩子為2*5即10,右孩子為2*5+1即11。
這個特點為什麼重要呢?它使得邏輯概念上的二叉樹可以方便的存儲到數組中,數組中的元素索引就對應節點的編號,樹中的父子關系通過其索引關系隱含維持,不需要單獨保持。比如說,上圖中的邏輯二叉樹,保存到數組中,其結構為:

父子關系是隱含的,比如對於第5個元素13,其父節點就是第2個元素15,左孩子就是第10個元素7,右孩子就是第11個元素4。
這種存儲二叉樹的方法與之前介紹的TreeMap是不一樣的,在TreeMap中,有一個單獨的內部類Entry,Entry有三個引用,分別指向父節點、左孩子、右孩子。
使用數組存儲,優點是很明顯的,節省空間,訪問效率高。
最大堆/最小堆
堆邏輯概念上是一顆完全二叉樹,而物理存儲上使用數組,除了這兩點,堆還有一定的順序要求。
之前介紹過排序二叉樹,排序二叉樹是完全有序的,每個節點都有確定的前驅和後繼,而且不能有重復元素。
與排序二叉樹不同,在堆中,可以有重復元素,元素間不是完全有序的,但對於父子節點之間,有一定的順序要求,根據順序分為兩種堆,一種是最大堆,另一種是最小堆。
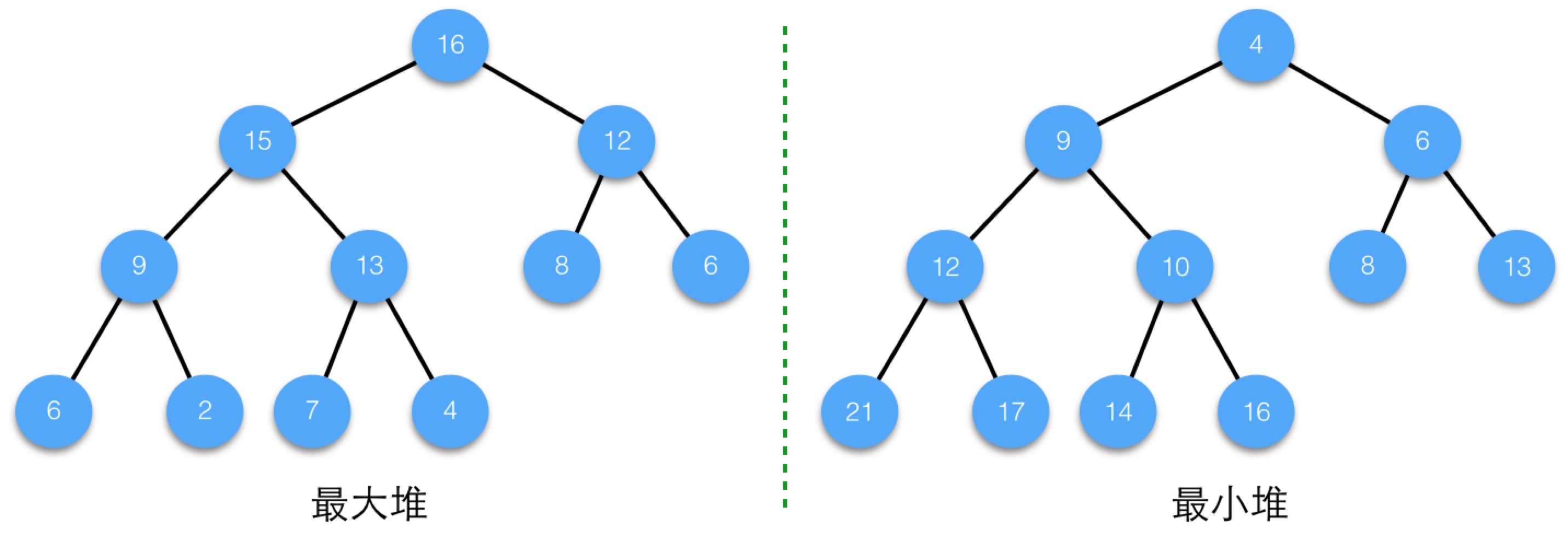
最大堆是指,每個節點都不大於其父節點。這樣,對每個父節點,一定不小於其所有孩子節點,而根節點就是所有節點中最大的,對每個子樹,子樹的根也是子樹所有節點中最大的。
最小堆與最大堆正好相反,每個節點都不小於其父節點。這樣,對每個父節點,一定不大於其所有孩子節點,而根節點就是所有節點中最小的,對每個子樹,子樹的根也是子樹所有節點中最小的。
我們看下圖示:
堆概念總結
總結來說,邏輯概念上,堆是完全二叉樹,父子節點間有特定順序,分為最大堆和最小堆,最大堆根是最大的,最小堆根是最小的,堆使用數組進行物理存儲。
這個數據結構為什麼就可以高效的解決之前我們說的問題呢?在回答之前,我們需要先看下,如何在堆上進行數據的基本操作,在操作過程中,如何保持堆的屬性不變。
堆的算法
下面,我們來看下,如何在堆上進行數據的基本操作。最大堆和最小堆的算法是類似的,我們以最小堆來說明。先來看如何添加元素。
添加元素
如果堆為空,則直接添加一個根就行了。我們假定已經有一個堆了,要在其中添加元素。基本步驟為:
我們來看個例子。下面是初始結構:
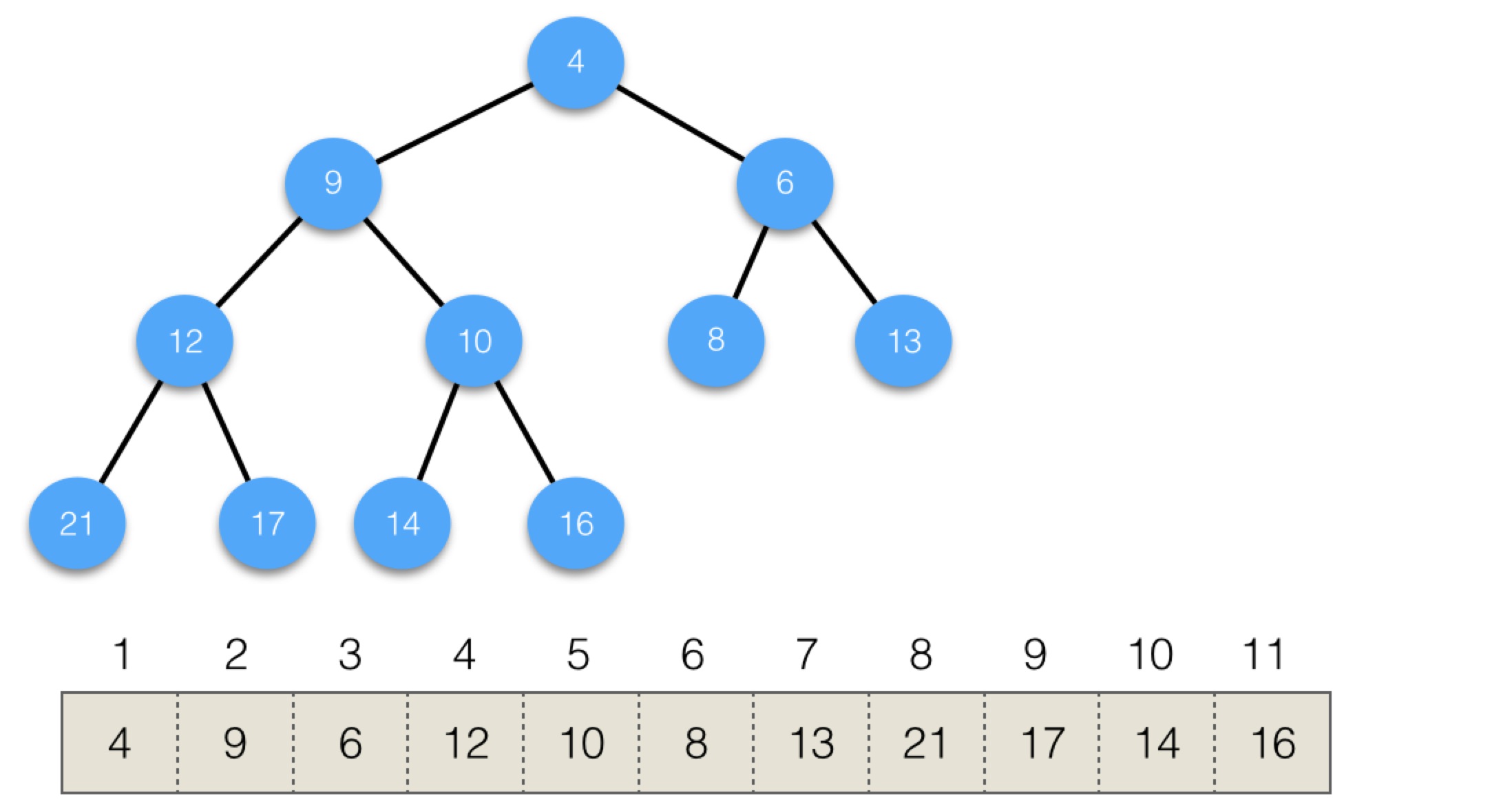
添加元素3,第一步後,結構變為:
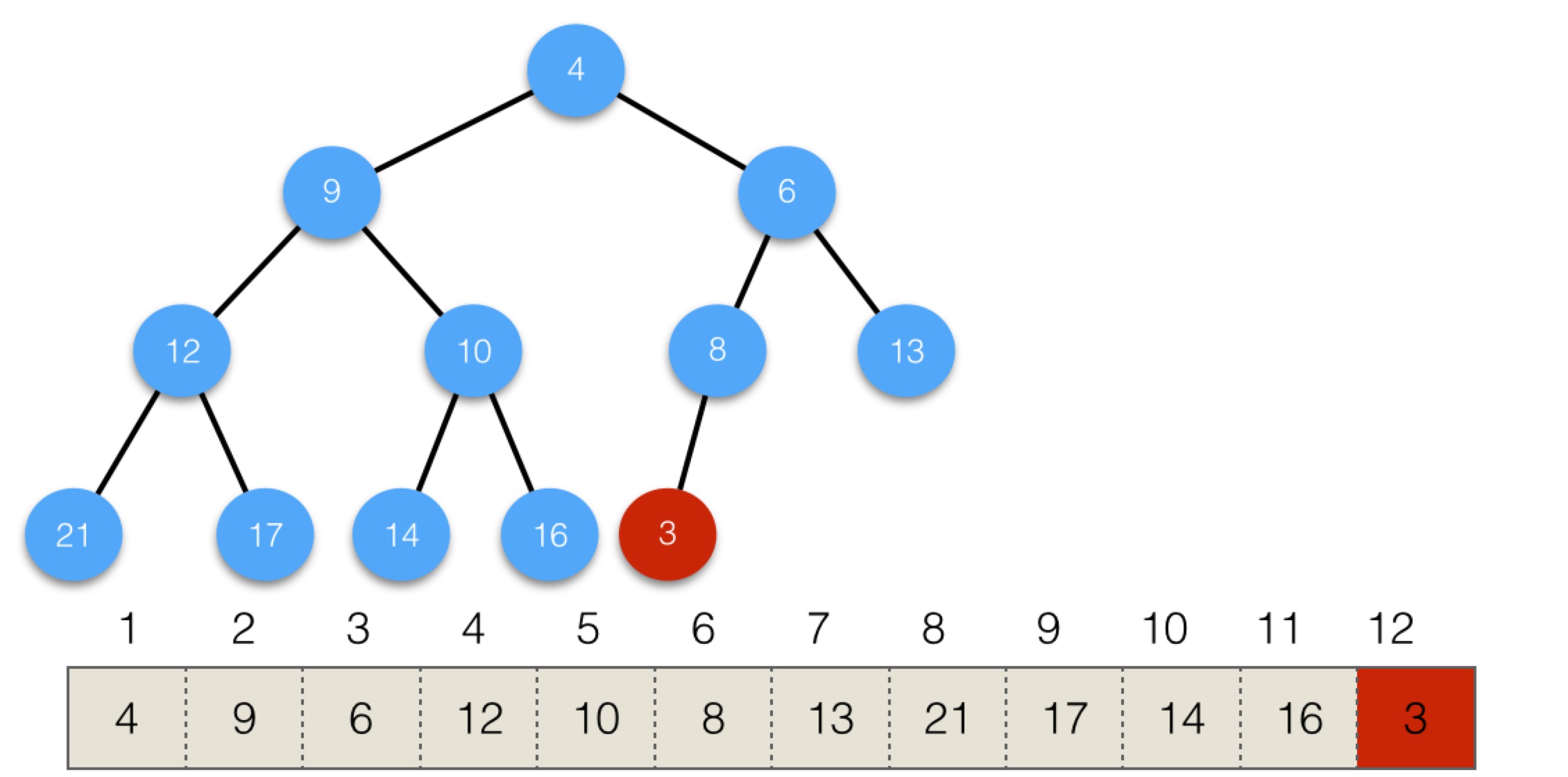
3小於父節點8,不滿足最小堆的性質,所以與父節點交換,會變為:
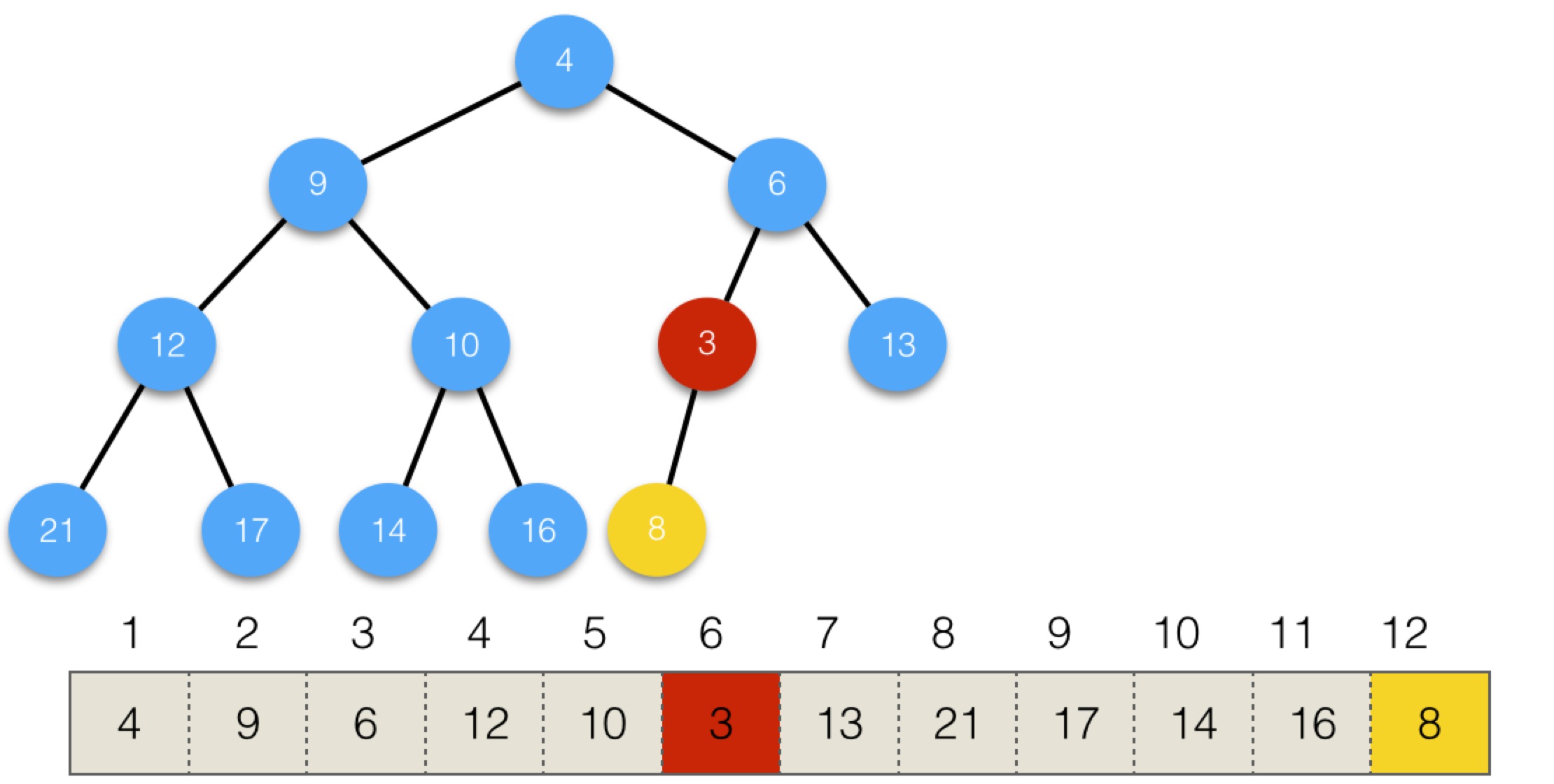
交換後,3還是小於父節點6,所以繼續交換,會變為:
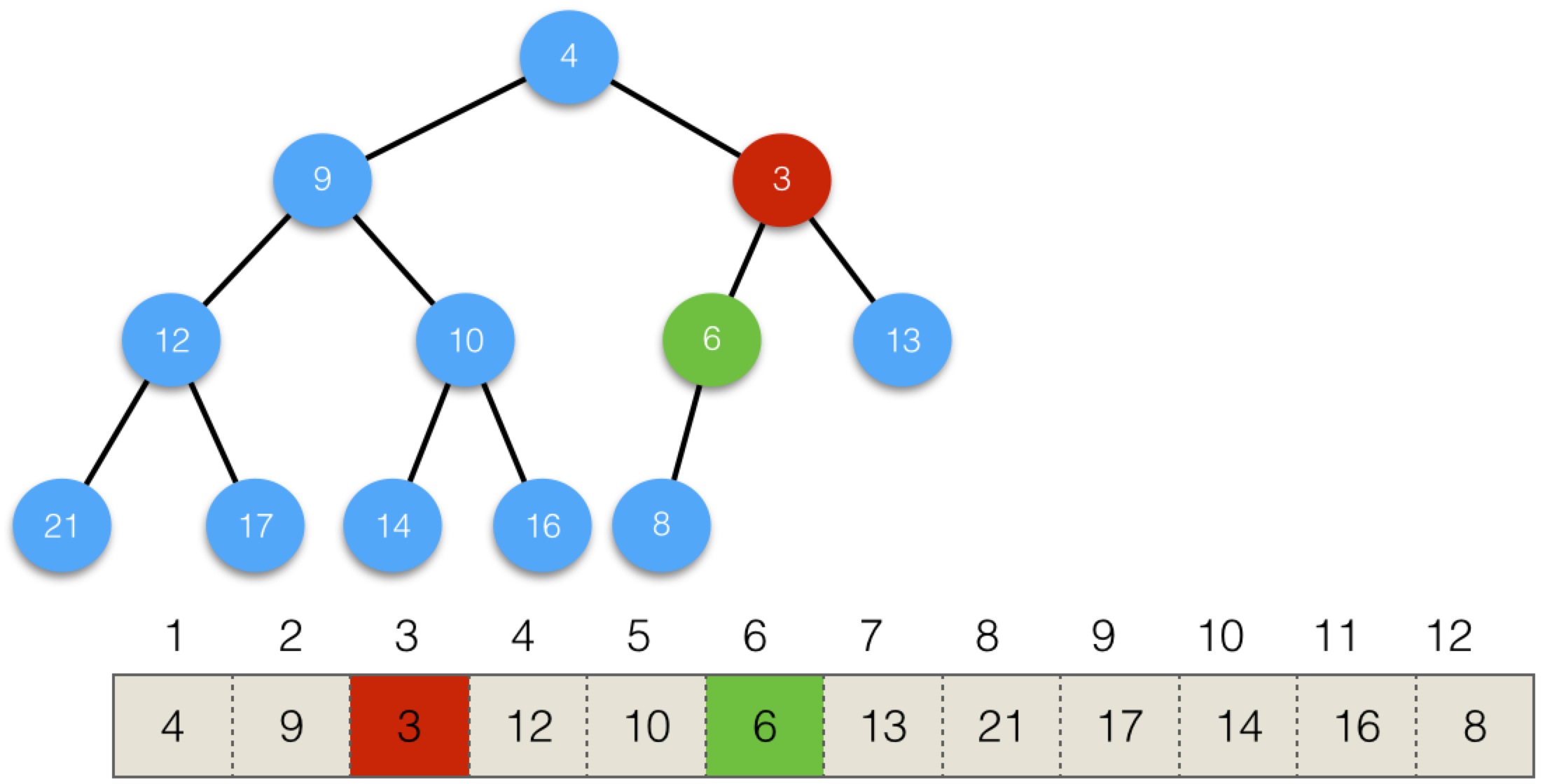
交換後,3還是小於父節點,也是根節點4,繼續交換,變為:
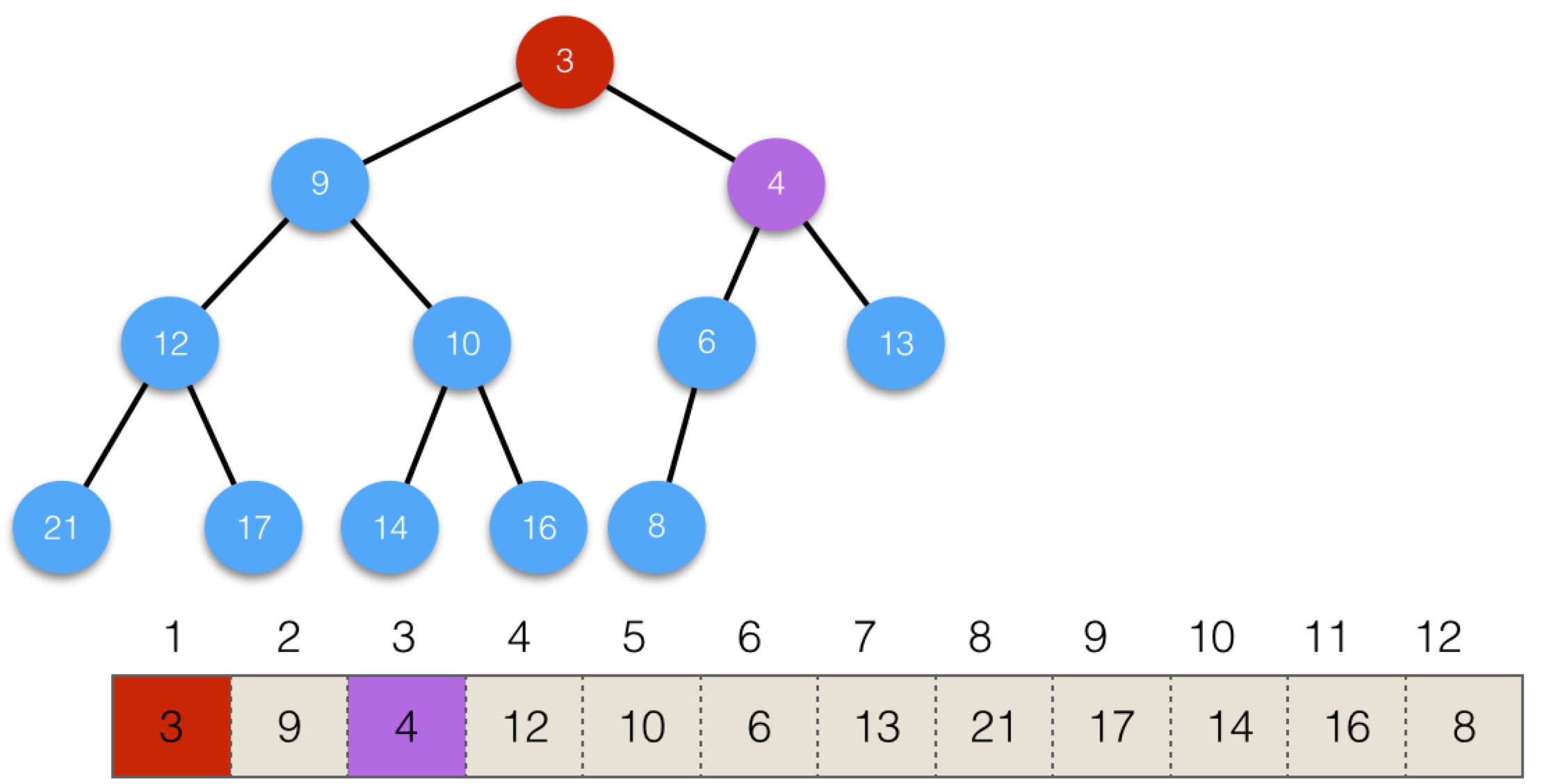
這時,調整就結束了,樹保持了堆的性質。
從以上過程可以看出,添加一個元素,需要比較和交換的次數最多為樹的高度,即log2(N),N為節點數。
這種自低向上比較、交換,使得樹重新滿足堆的性質的過程,我們稱之為siftup。
從頭部刪除元素
在隊列中,一般是從頭部刪除元素,Java中用堆實現優先級隊列,我們來看下如何在堆中刪除頭部,其基本步驟為:
我們來看個例子。下面是初始結構:
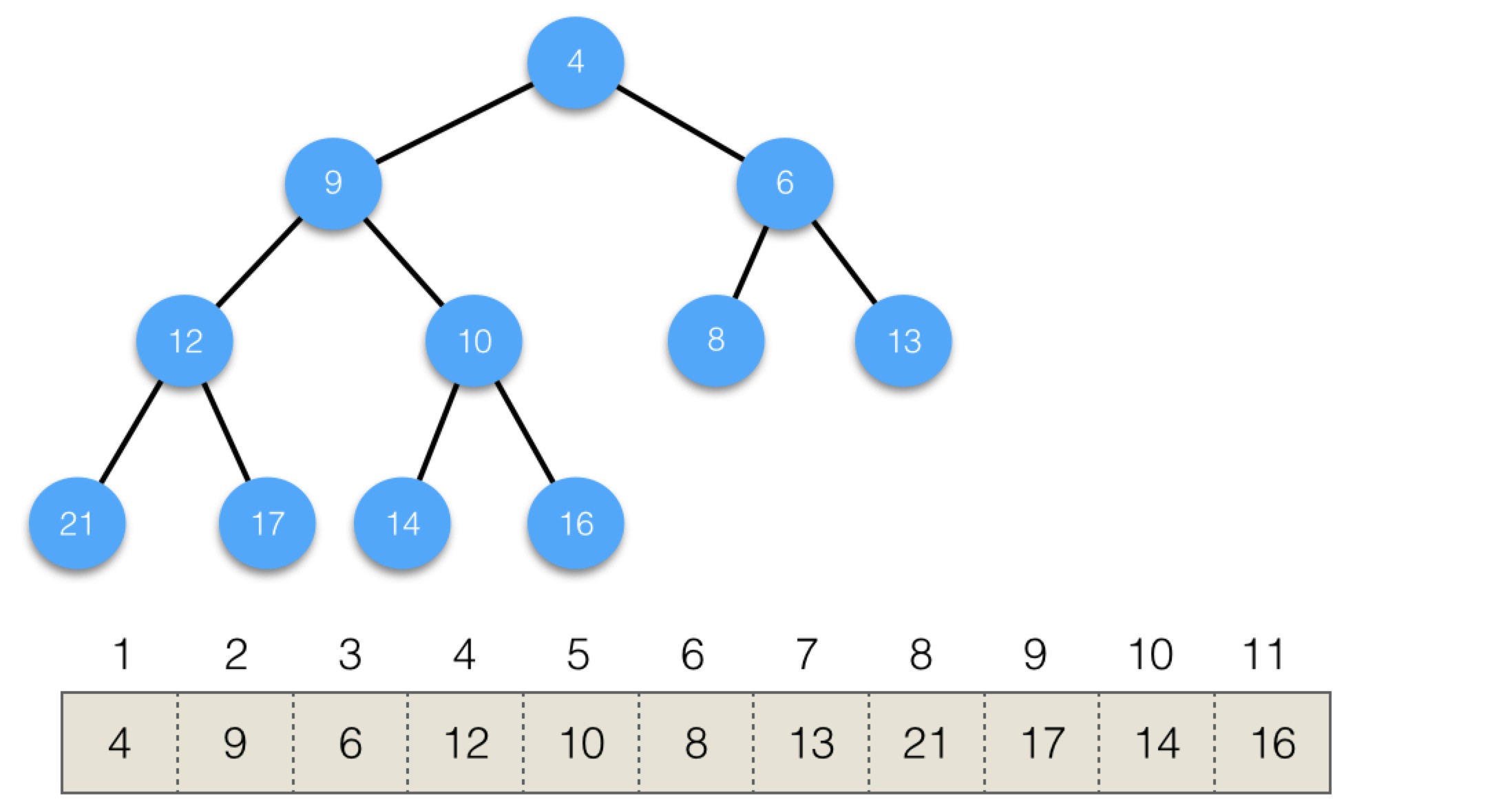
執行第一步,用最後元素替換頭部,會變為:
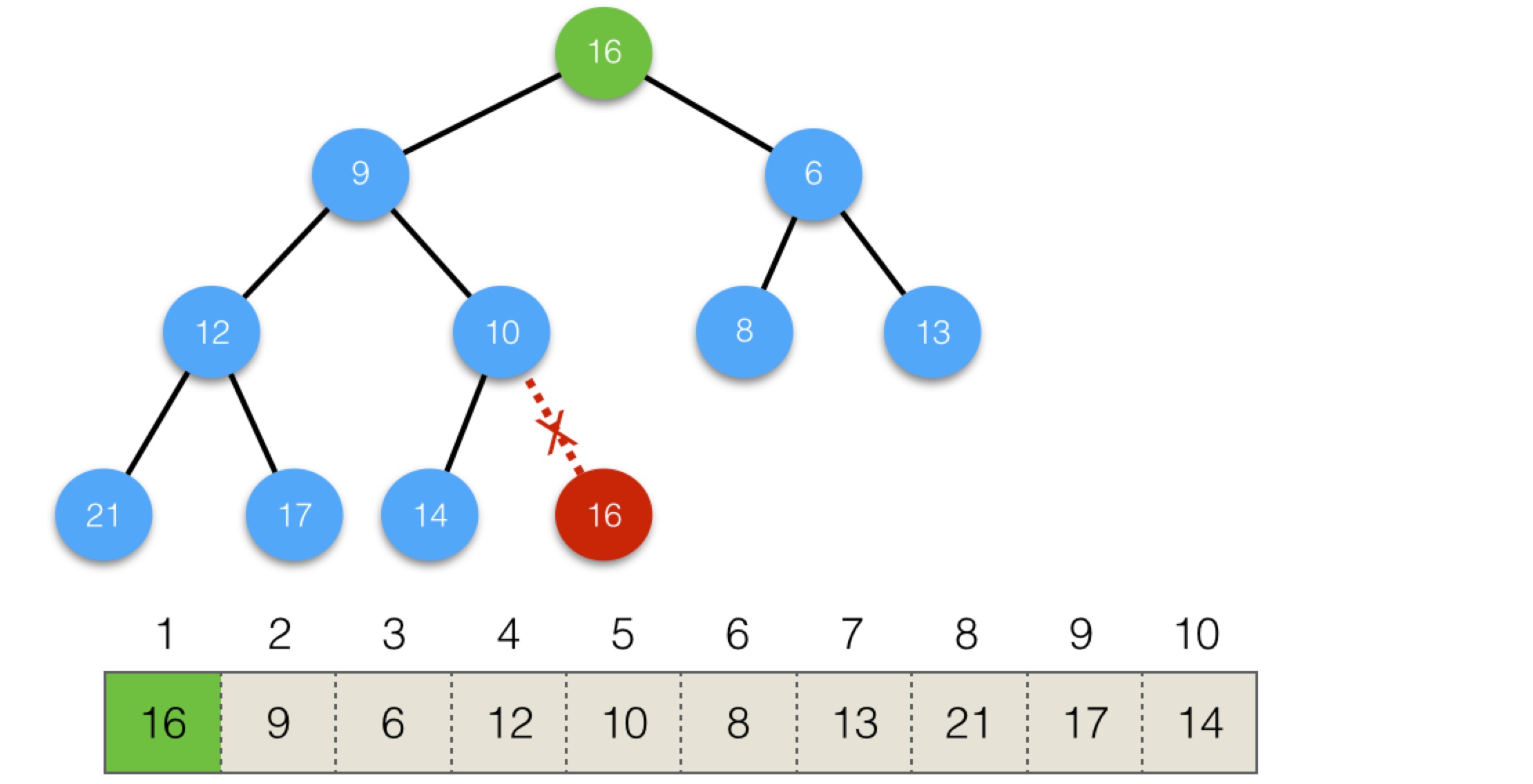
現在根節點16小於孩子節點,與更小的孩子節點6進行替換,結構會變為:
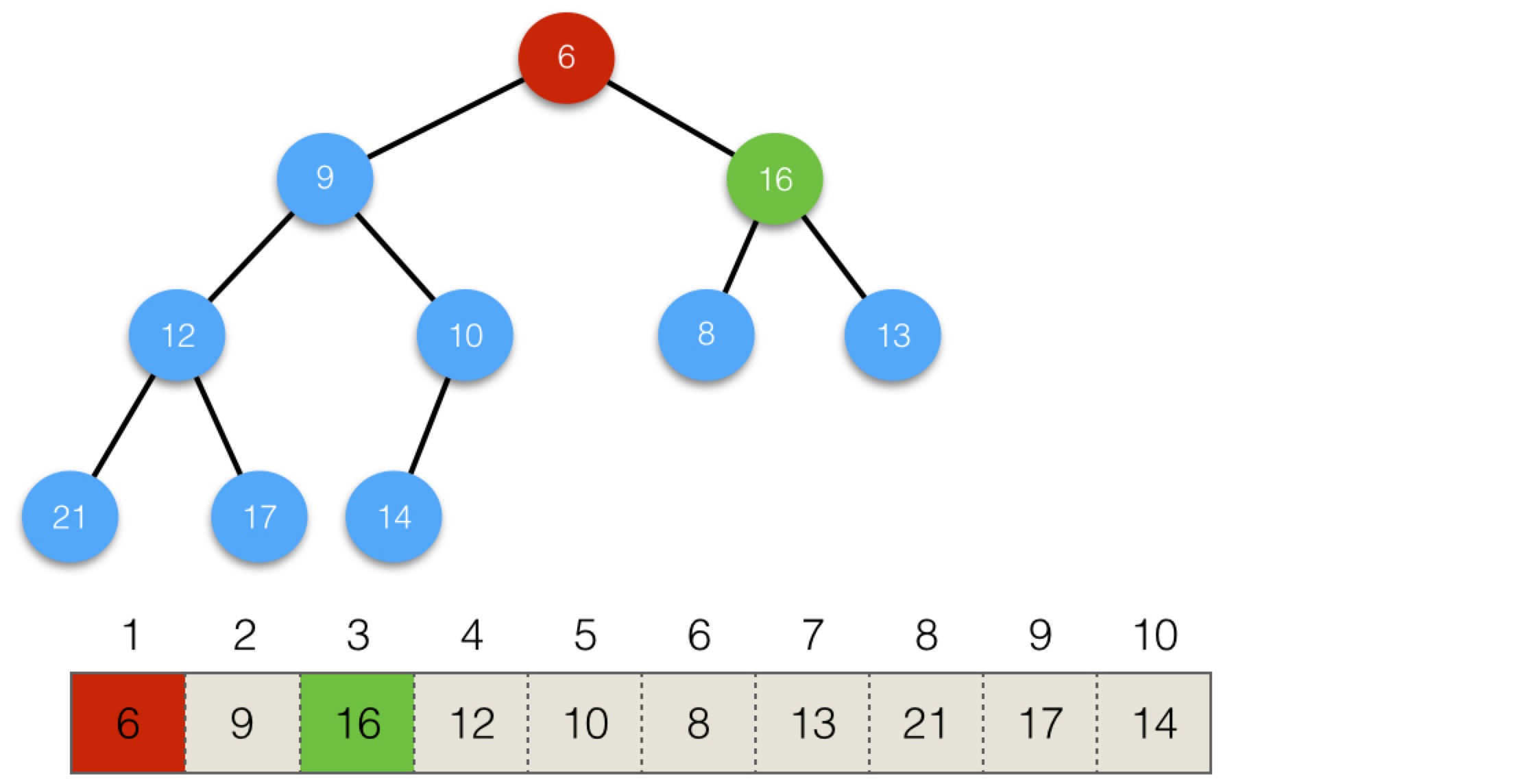
16還是小於孩子節點,與更小的孩子8進行交換,結構會變為:
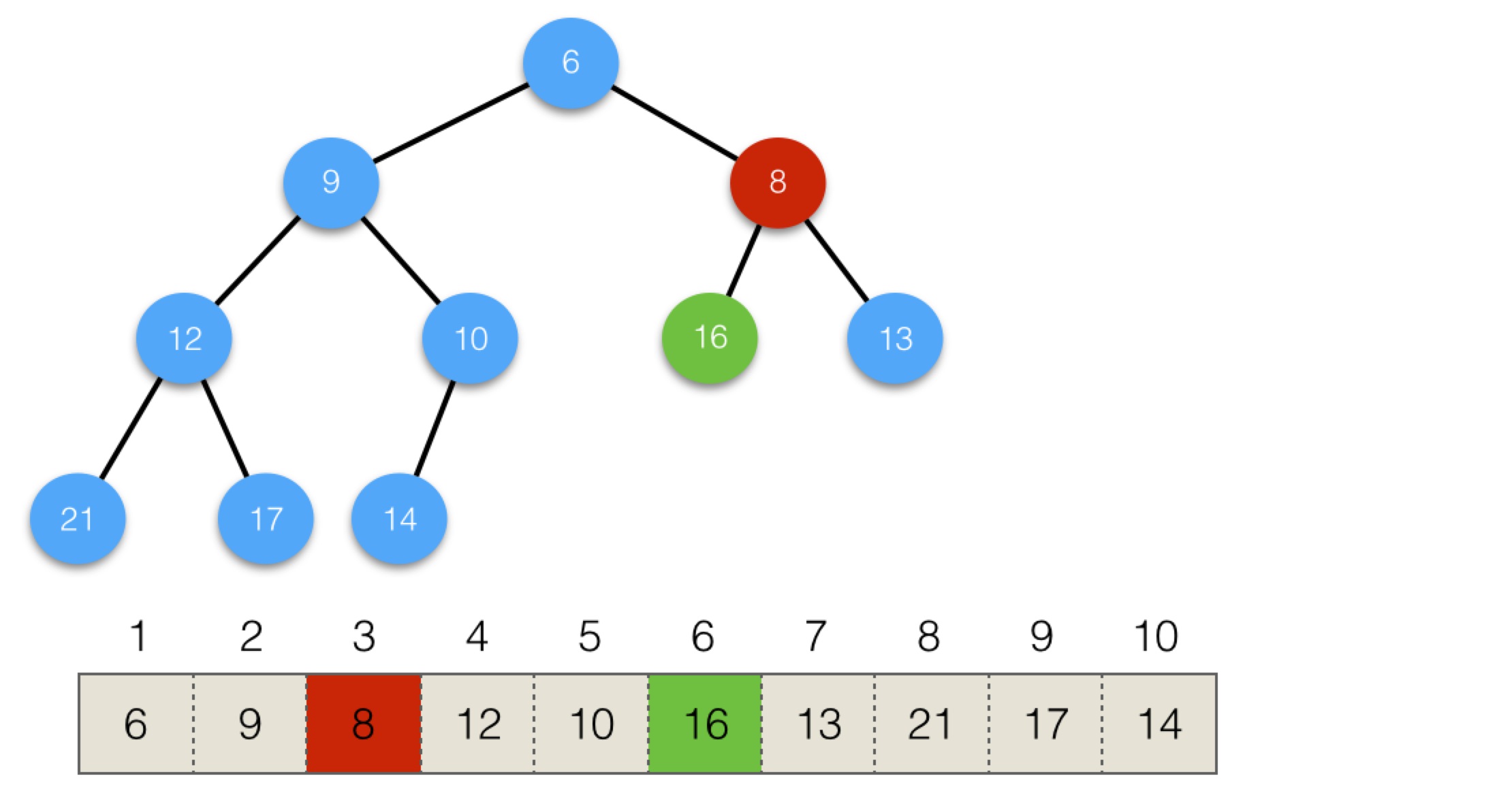
此時,就滿足堆的性質了。
從中間刪除元素
那如果需要從中間刪除某個節點呢?與從頭部刪除一樣,都是先用最後一個元素替換待刪元素。不過替換後,有兩種情況,如果該元素大於某孩子節點,則需向下調整(siftdown),否則,如果小於父節點,則需向上調整(siftup)。
我們來看個例子,刪除值為21的節點,第一步如下圖所示:
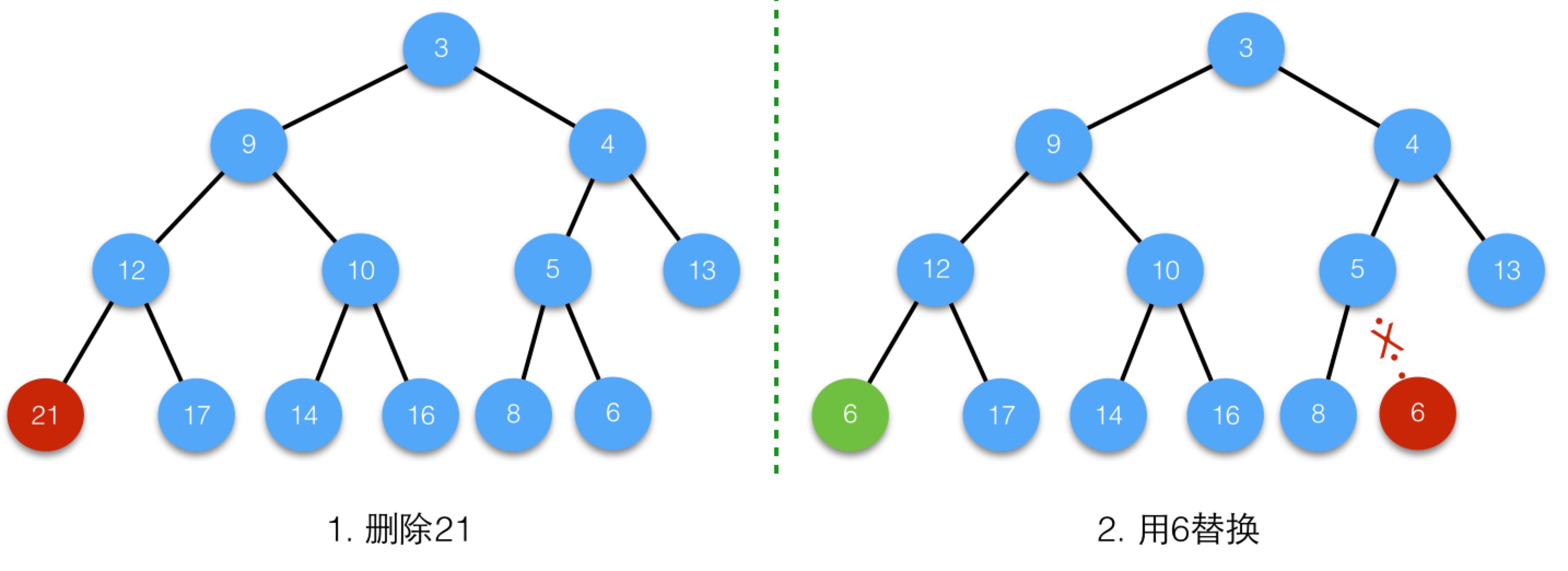
替換後,6沒有子節點,小於父節點12,執行向上調整siftup過程,最後結果為:
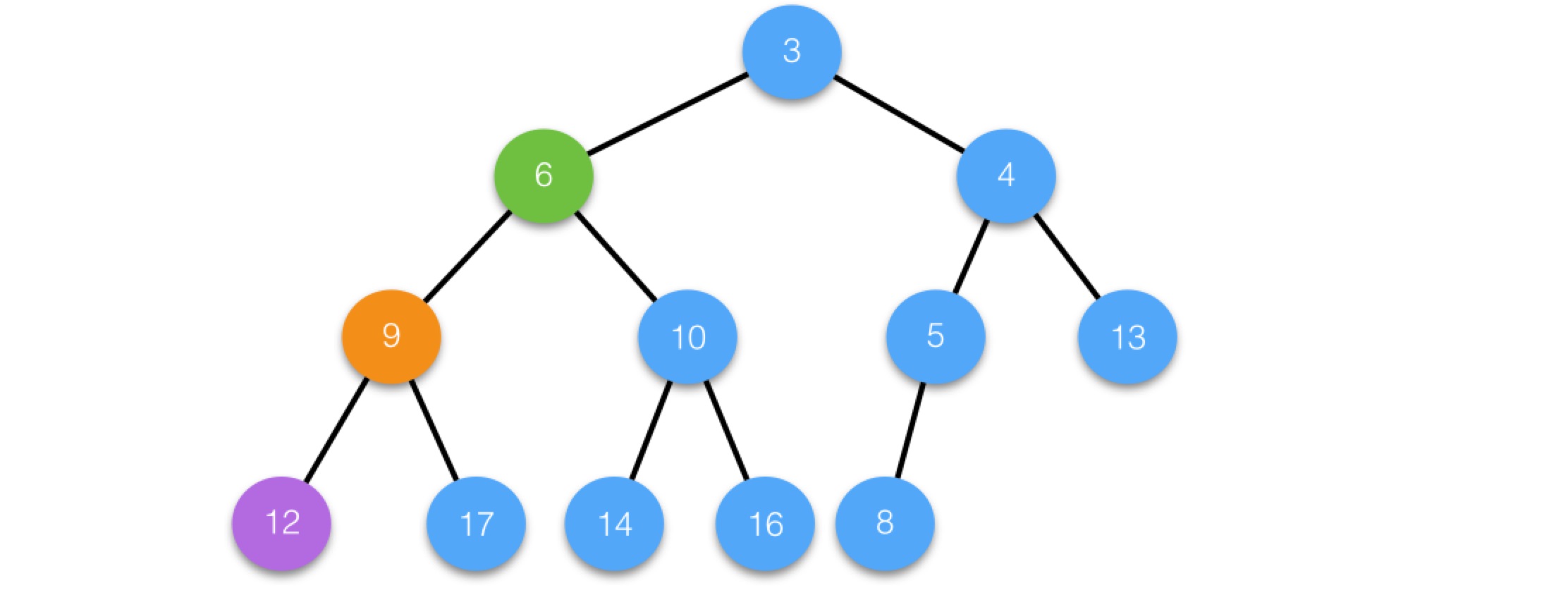
我們再來看個例子,刪除值為9的節點,第一步如下圖所示:
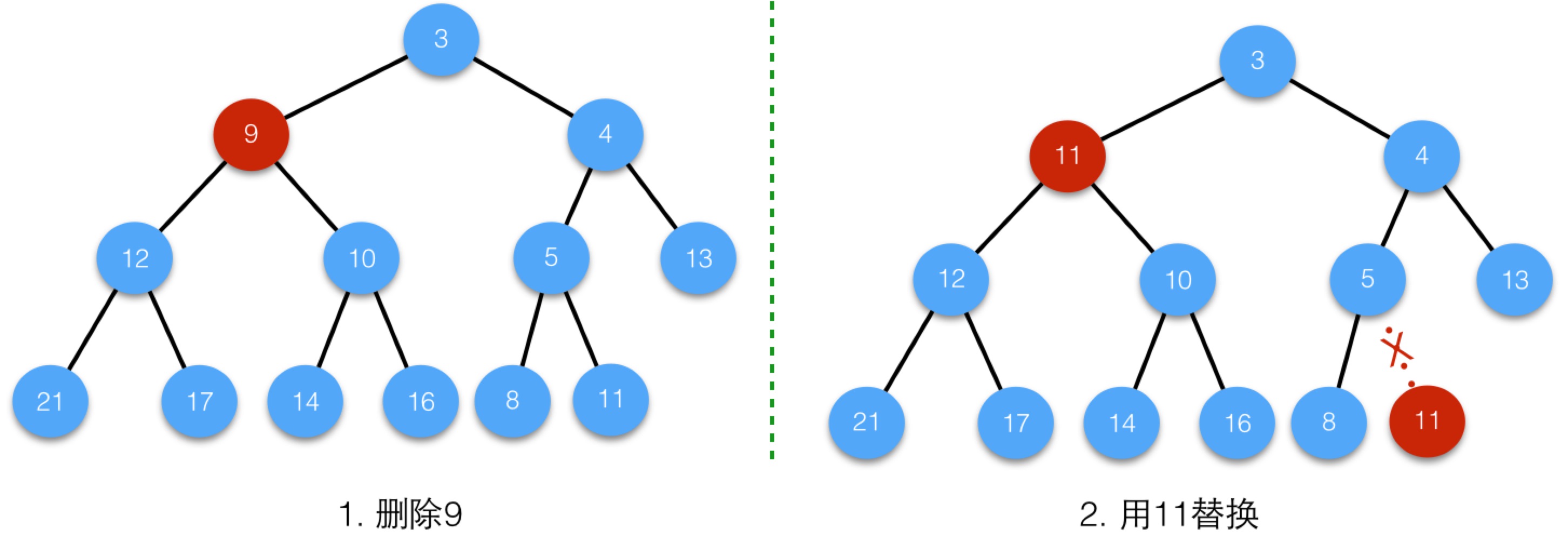
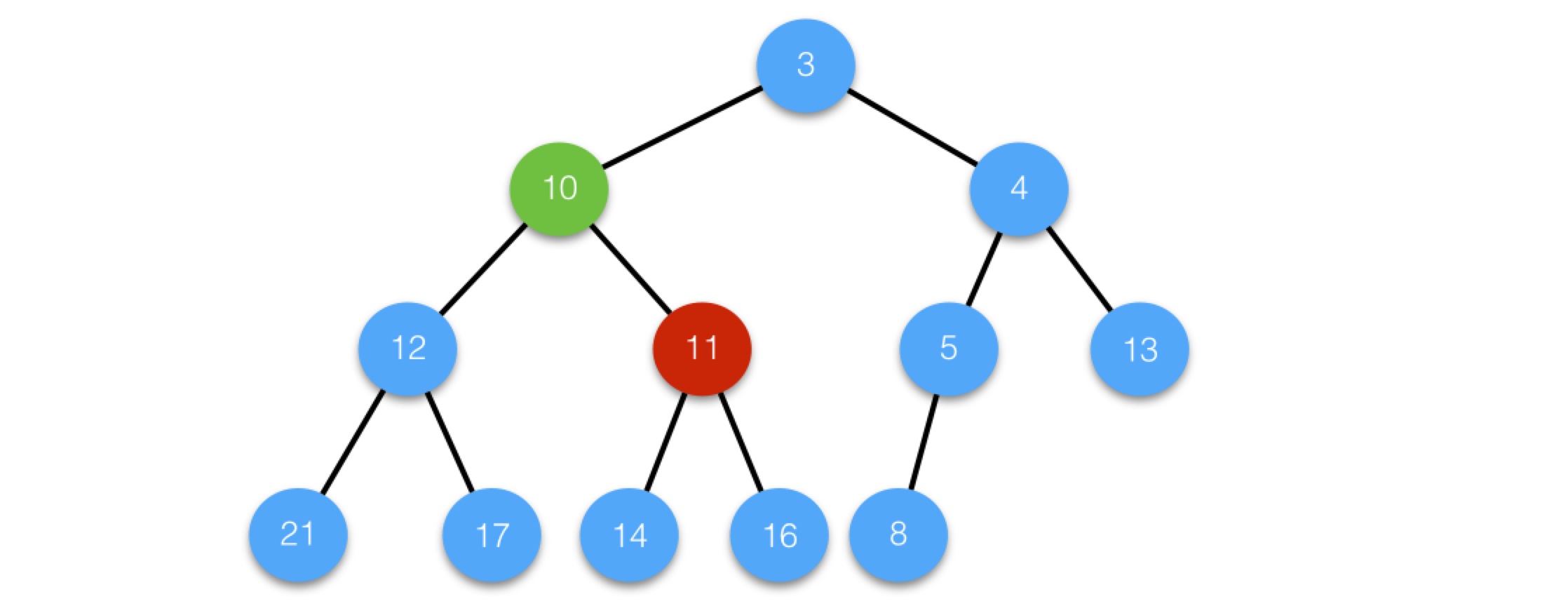
交換後,11小於右孩子10,所以執行siftdown過程,執行結束後為:
構建初始堆
給定一個無序數組,如何使之成為一個最小堆呢?將普通無序數組變為堆的過程我們稱之為heapify。
基本思路是,從最後一個非葉子節點開始,一直往前直到根,對每個節點,執行向下調整siftdown。換句話說,是自底向上,先使每個最小子樹為堆,然後每對左右子樹和其父節點合並,調整為更大的堆,因為每個子樹已經為堆,所以調整就是對父節點執行siftdown,就這樣一直合並調整直到根。這個算法的偽代碼是:
void heapify() {
for (int i=size/2; i >= 1; i--)
siftdown(i);
}
size表示節點個數, 節點編號從1開始,size/2表示第一個非葉節點的編號。
這個構建的時間效率為O(N),N為節點個數,具體就不證明了。
查找和遍歷
在堆中進行查找沒有特殊的算法,就是從數組的頭找到尾,效率為O(N)。
在堆中進行遍歷也是類似的,堆就是數組,堆的遍歷就是數組的遍歷,第一個元素是最大值或最小值,但後面的元素沒有特定的順序。
需要說明的是,如果是逐個從頭部刪除元素,堆可以確保輸出是有序的。
算法小結
以上就是堆操作的主要算法:
小結
本節介紹了堆這一數據結構的基本概念和算法。
堆是一種比較神奇的數據結構,概念上是樹,存儲為數組,父子有特殊順序,根是最大值/最小值,構建/添加/刪除效率都很高,可以高效解決很多問題。
但在Java中,堆到底是如何實現的呢?本文開頭提到的那些問題,用堆到底如何解決呢?讓我們在接下來的幾節中繼續探索。
---------------
未完待續,查看最新文章,敬請關注微信公眾號“老馬說編程”(掃描下方二維碼),從入門到高級,深入淺出,老馬和你一起探索Java編程及計算機技術的本質。用心原創,保留所有版權。
