40節介紹了HashMap,我們提到,HashMap有一個重要局限,鍵值對之間沒有特定的順序,我們還提到,Map接口有另一個重要的實現類TreeMap,在TreeMap中,鍵值對之間按鍵有序,TreeMap的實現基礎是排序二叉樹,上節我們介紹了排序二叉樹的基本概念和算法,本節我們來詳細討論TreeMap。
除了Map接口,因為有序,TreeMap還實現了更多接口和方法,下面,我們先來看TreeMap的用法,然後探討其內部實現。
基本用法
構造方法
TreeMap有兩個基本構造方法:
public TreeMap() public TreeMap(Comparator<? super K> comparator)
第一個為默認構造方法,如果使用默認構造方法,要求Map中的鍵實現Comparabe接口,TreeMap內部進行各種比較時會調用鍵的Comparable接口中的compareTo方法。
第二個接受一個比較器對象comparator,如果comparator不為null,在TreeMap內部進行比較時會調用這個comparator的compare方法,而不再調用鍵的compareTo方法,也不再要求鍵實現Comparable接口。
應該用哪一個呢?第一個更為簡單,但要求鍵實現Comparable接口,且期望的排序和鍵的比較結果是一致的,第二個更為靈活,不要求鍵實現Comparable接口,比較器可以用靈活復雜的方式進行實現。
需要強調的是,TreeMap是按鍵而不是按值有序,無論哪一種,都是對鍵而非值進行比較。
除了這兩個基本構造方法,TreeMap還有如下構造方法:
public TreeMap(Map<? extends K, ? extends V> m) public TreeMap(SortedMap<K, ? extends V> m)
關於SortedMap接口,它擴展了Map接口,表示有序的Map,它有一個comparator()方法,返回其比較器,待會我們會進一步介紹。
這兩個構造方法都是接受一個已有的Map,將其所有鍵值對添加到當前TreeMap中來,區別在於,第一個構造方法中,比較器會設為null,而第二個,比較器會設為和參數SortedMap中的一樣。
接下來,我們來看一些簡單的使用TreeMap的例子。
基本例子
代碼為:
Map<String, String> map = new TreeMap<>();
map.put("a", "abstract");
map.put("c", "call");
map.put("b", "basic");
map.put("T", "tree");
for(Entry<String,String> kv : map.entrySet()){
System.out.print(kv.getKey()+"="+kv.getValue()+" ");
}
創建了一個TreeMap,但只是當做Map使用,不過迭代時,其輸出卻是按鍵排序的,輸出為:
T=tree a=abstract b=basic c=call
T排在最前面,是因為大寫字母都小於小寫字母。如果希望忽略大小寫呢?可以傳遞一個比較器,String類有一個靜態成員CASE_INSENSITIVE_ORDER,它就是一個忽略大小寫的Comparator對象,替換第一行代碼為:
Map<String, String> map = new TreeMap<>(String.CASE_INSENSITIVE_ORDER);
輸出就會變為:
a=abstract b=basic c=call T=tree
正常排序是從小到大,如果希望逆序呢?可以傳遞一個不同的Comparator對象,第一行代碼可以替換為:
Map<String, String> map = new TreeMap<>(new Comparator<String>(){
@Override
public int compare(String o1, String o2) {
return o2.compareTo(o1);
}
});
這樣,輸出會變為:
c=call b=basic a=abstract T=tree
為什麼這樣就可以逆序呢?正常排序中,compare方法內,是o1.compareTo(o2),兩個對象翻過來,自然就是逆序了,Collections類有一個靜態方法reverseOrder()可以返回一個逆序比較器,也就是說,上面代碼也可以替換為:
Map<String, String> map = new TreeMap<>(Collections.reverseOrder());
如果希望逆序且忽略大小寫呢?第一行可以替換為:
Map<String, String> map = new TreeMap<>(
Collections.reverseOrder(String.CASE_INSENSITIVE_ORDER));
需要說明的是,TreeMap使用鍵的比較結果對鍵進行排重,即使鍵實際上不同,但只要比較結果相同,它們就會被認為相同,鍵只會保存一份。比如,如下代碼:
Map<String, String> map = new TreeMap<>(String.CASE_INSENSITIVE_ORDER);
map.put("T", "tree");
map.put("t", "try");
for(Entry<String,String> kv : map.entrySet()){
System.out.print(kv.getKey()+"="+kv.getValue()+" ");
}
看上去有兩個不同的鍵"T"和"t",但因為比較器忽略大小寫,所以只會有一個,輸出會是:
T=try
鍵為第一次put時的,這裡即"T",而值為最後一次put時的,這裡即"try"。
日期例子
我們再來看一個例子,鍵為字符串形式的日期,值為一個統計數字,希望按照日期輸出,代碼為:
Map<String, Integer> map = new TreeMap<>();
map.put("2016-7-3", 100);
map.put("2016-7-10", 120);
map.put("2016-8-1", 90);
for(Entry<String,Integer> kv : map.entrySet()){
System.out.println(kv.getKey()+","+kv.getValue());
}
輸出為:
2016-7-10,120 2016-7-3,100 2016-8-1,90
7月10號的排在了7月3號的前面,與期望的不符,這是因為,它們是按照字符串比較的,按字符串,2016-7-10就是小於2016-7-3,因為第一個不同之處1小於3。
怎麼解決呢?可以使用一個自定義的比較器,將字符串轉換為日期,按日期進行比較,第一行代碼可以改為:
Map<String, Integer> map = new TreeMap<>(new Comparator<String>() {
SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd");
@Override
public int compare(String o1, String o2) {
try {
return sdf.parse(o1).compareTo(sdf.parse(o2));
} catch (ParseException e) {
e.printStackTrace();
return 0;
}
}
});
這樣,輸出就符合期望了,會變為:
2016-7-3,100 2016-7-10,120 2016-8-1,90
基本用法小結
以上就是TreeMap的基本用法,與HashMap相比:
不過,由於TreeMap按鍵有序,它還支持更多接口和方法,具體來說,它還實現了SortedMap和NavigableMap接口,而NavigableMap接口擴展了SortedMap,我們來看一下這兩個接口。
高級用法
SortedMap接口
SortedMap接口的定義為:
public interface SortedMap<K,V> extends Map<K,V> {
Comparator<? super K> comparator();
SortedMap<K,V> subMap(K fromKey, K toKey);
SortedMap<K,V> headMap(K toKey);
SortedMap<K,V> tailMap(K fromKey);
K firstKey();
K lastKey();
}
firstKey返回第一個鍵,而lastKey返回最後一個鍵。
headMap/tailMap/subMap都返回一個視圖,視圖中包括一部分鍵值對,它們的區別在於鍵的取值范圍:
NavigableMap接口
NavigableMap擴展了SortedMap,主要增加了一些查找鄰近鍵的方法,比如:
Map.Entry<K,V> floorEntry(K key); Map.Entry<K,V> lowerEntry(K key); Map.Entry<K,V> ceilingEntry(K key); Map.Entry<K,V> higherEntry(K key);
參數key對應的鍵不一定存在,但這些方法可能都有返回值,它們都返回一個鄰近鍵值對,它們的區別在於,這個鄰近鍵與參數key的關系。
如果沒有對應的鄰近鍵,返回值為null。這些方法也都有對應的只返回鍵的方法:
K floorKey(K key); K lowerKey(K key); K ceilingKey(K key); K higherKey(K key);
相比SortedMap中的方法headMap/tailMap/subMap,NavigableMap也增加了一些方法,以更為明確的方式指定返回值中是否包含邊界值,如:
NavigableMap<K,V> headMap(K toKey, boolean inclusive);
NavigableMap<K,V> tailMap(K fromKey, boolean inclusive);
NavigableMap<K,V> subMap(K fromKey, boolean fromInclusive,
K toKey, boolean toInclusive);
相比SortedMap中對頭尾鍵的基本操作,NavigableMap增加了如下方法:
Map.Entry<K,V> firstEntry(); Map.Entry<K,V> lastEntry(); Map.Entry<K,V> pollFirstEntry(); Map.Entry<K,V> pollLastEntry();
firstEntry返回第一個鍵值對,lastEntry返回最後一個。pollFirstEntry刪除並返回第一個鍵值對,pollLastEntry刪除並返回最後一個。
此外,NavigableMap有如下方法,可以方便的逆序訪問:
NavigableMap<K,V> descendingMap(); NavigableSet<K> descendingKeySet();
示例代碼
我們看一段簡單的示例代碼,邏輯比較簡單,就不解釋了,主要是增強直觀感受,其中輸出用注釋說明了:
NavigableMap<String, String> map = new TreeMap<>();
map.put("a", "abstract");
map.put("f", "final");
map.put("c", "call");
//輸出:a=abstract
System.out.println(map.firstEntry());
//輸出:f=final
System.out.println(map.lastEntry());
//輸出:c=call
System.out.println(map.floorEntry("d"));
//輸出:f=final
System.out.println(map.ceilingEntry("d"));
//輸出:{c=call, a=abstract}
System.out.println(map.descendingMap()
.subMap("d", false, "a", true));
了解了TreeMap的用法,接下來,我們來看TreeMap的實現原理。
基本實現原理
TreeMap內部是用紅黑樹實現的,紅黑樹是一種大致平衡的排序二叉樹,上節我們介紹了排序二叉樹的基本概念和算法,本節我們主要看TreeMap的一些代碼實現,先來看TreeMap的內部組成。
內部組成
TreeMap內部主要有如下成員:
private final Comparator<? super K> comparator; private transient Entry<K,V> root = null; private transient int size = 0;
comparator就是比較器,在構造方法中傳遞,如果沒傳,就是null。size為當前鍵值對個數。root指向樹的根節點,從根節點可以訪問到每個節點,節點的類型為Entry。Entry是TreeMap的一個內部類,其內部成員和構造方法為:
static final class Entry<K,V> implements Map.Entry<K,V> {
K key;
V value;
Entry<K,V> left = null;
Entry<K,V> right = null;
Entry<K,V> parent;
boolean color = BLACK;
/**
* Make a new cell with given key, value, and parent, and with
* {@code null} child links, and BLACK color.
*/
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
}
每個節點除了鍵(key)和值(value)之外,還有三個引用,分別指向其左孩子(left)、右孩子(right)和父節點(parent),對於根節點,父節點為null,對於葉子節點,孩子節點都為null,還有一個成員color表示顏色,TreeMap是用紅黑樹實現的,每個節點都有一個顏色,非黑即紅。
了解了TreeMap的內部組成,我們來看一些主要方法的實現代碼。
保存鍵值對
put方法的代碼稍微有點長,我們分段來看,先看第一段,添加第一個節點的情況:
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
...
當添加第一個節點時,root為null,執行的就是這段代碼,主要就是新建一個節點,設置root指向它,size設置為1,modCount++的含義與之前幾節介紹的類似,用於迭代過程中檢測結構性變化。
令人費解的是compare調用,compare(key, key);,key與key比,有什麼意義呢?我們看compare方法的代碼:
final int compare(Object k1, Object k2) {
return comparator==null ? ((Comparable<? super K>)k1).compareTo((K)k2)
: comparator.compare((K)k1, (K)k2);
}
其實,這裡的目的不是為了比較,而是為了檢查key的類型和null,如果類型不匹配或為null,compare方法會拋出異常。
如果不是第一次添加,會執行後面的代碼,添加的關鍵步驟是尋找父節點,找父節點根據是否設置了comparator分為兩種情況,我們先來看設置了的情況,代碼為:
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
尋找是一個從根節點開始循環的過程,在循環中,cmp保存比較結果,t指向當前比較節點,parent為t的父節點,循環結束後parent就是要找的父節點。
t一開始指向根節點,從根節點開始比較鍵,如果小於根節點,就將t設為左孩子,與左孩子比較,大於就與右孩子比較,就這樣一直比,直到t為null或比較結果為0。如果比較結果為0,表示已經有這個鍵了,設置值,然後返回。如果t為null,則當退出循環時,parent就指向待插入節點的父節點。
我們再來看沒有設置comparator的情況,代碼為:
else {
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
基本邏輯是一樣的,當退出循環時parent指向父節點,只是,如果沒有設置comparator,則假設key一定實現了Comparable接口,使用Comparable接口的compareTo方法進行比較。
找到父節點後,就是新建一個節點,根據新的鍵與父節點鍵的比較結果,插入作為左孩子或右孩子,並增加size和modCount,代碼如下:
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);
size++;
modCount++;
代碼大部分都容易理解,不過,裡面有一行重要調用fixAfterInsertion(e);,它就是在調整樹的結構,使之符合紅黑樹的約束,保持大致平衡,其代碼我們就不介紹了。
稍微總結一下,其基本思路就是,循環比較找到父節點,並插入作為其左孩子或右孩子,然後調整保持樹的大致平衡。
根據鍵獲取值
代碼為:
public V get(Object key) {
Entry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
就是根據key找對應節點p,找到節點後獲取值p.value,來看getEntry的代碼:
final Entry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}
如果comparator不為空,調用單獨的方法getEntryUsingComparator,否則,假定key實現了Comparable接口,使用接口的compareTo方法進行比較,找的邏輯也很簡單,從根開始找,小於往左邊找,大於往右邊找,直到找到為止,如果沒找到,返回null。getEntryUsingComparator方法的邏輯是類似,就不贅述了。
查看是否包含某個值
TreeMap可以高效的按鍵進行查找,但如果要根據值進行查找,則需要遍歷,我們來看代碼:
public boolean containsValue(Object value) {
for (Entry<K,V> e = getFirstEntry(); e != null; e = successor(e))
if (valEquals(value, e.value))
return true;
return false;
}
主體就是一個循環遍歷,getFirstEntry方法返回第一個節點,successor方法返回給定節點的後繼節點,valEquals就是比較值,從第一個節點開始,逐個進行比較,直到找到為止,如果循環結束也沒找到則返回false。
getFirstEntry的代碼為:
final Entry<K,V> getFirstEntry() {
Entry<K,V> p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
}
代碼很簡單,第一個節點就是最左邊的節點。
上節我們介紹過找後繼的算法,successor的具體代碼為:
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
如上節後繼算法所述,有兩種情況:
代碼與算法是對應的,就不再贅述了,下面重復一下上節的一個後繼圖(綠色箭頭表示後繼)以方便對照:
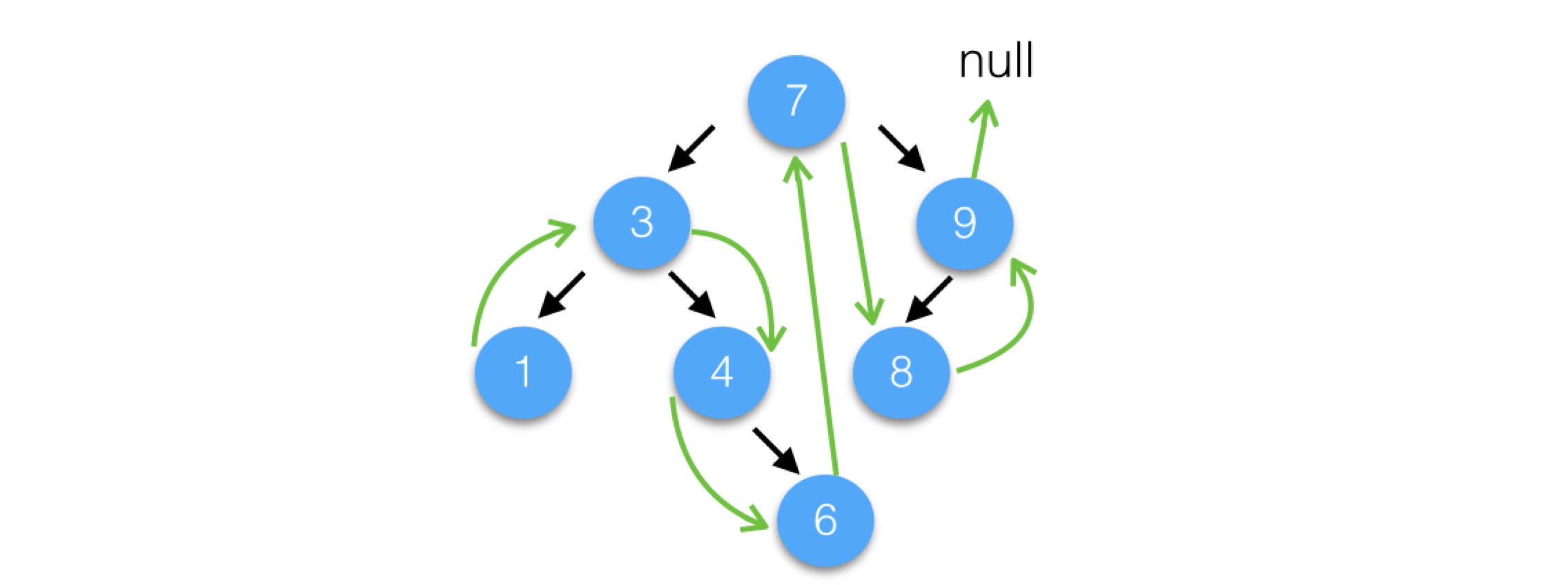
根據鍵刪除鍵值對
刪除的代碼為:
public V remove(Object key) {
Entry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
根據key找到節點,調用deleteEntry刪除節點,然後返回原來的值。
上節介紹過節點刪除的算法,節點有三種情況:
deleteEntry的具體代碼也稍微有點長,我們分段來看:
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
這裡處理的就是兩個孩子的情況,s為後繼,當前節點p的key和value設置為了s的key和value,然後將待刪節點p指向了s,這樣就轉換為了一個孩子或葉子節點的情況。
再往下看一個孩子情況的代碼:
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
p為待刪節點,replacement為要替換p的孩子節點,主體代碼就是在p的父節點p.parent和replacement之間建立鏈接,以替換p.parent和p原來的鏈接,如果p.parent為null,則修改root以指向新的根。fixAfterDeletion重新平衡樹。
最後來看葉子節點的情況:
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
再具體分為兩種情況,一種是刪除最後一個節點,修改root為null,否則就是根據待刪節點是父節點的左孩子還是右孩子,相應的設置孩子節點為null。
實現原理小結
以上就是TreeMap的基本實現原理,與上節介紹的排序二叉樹的基本概念和算法是一致的,只是TreeMap用了紅黑樹。
TreeMap特點分析
與HashMap相比,TreeMap同樣實現了Map接口,但內部使用紅黑樹實現,紅黑樹是統計效率比較高的大致平衡的排序二叉樹,這決定了它有如下特點:
應該用HashMap還是TreeMap呢?不要求排序,優先考慮HashMap,要求排序,考慮TreeMap。
小結
本節介紹了TreeMap的用法和實現原理,在用法方面,它實現了Map接口,但按鍵有序,同樣實現了SortedMap和NavigableMap接口,在內部實現上,它使用紅黑樹,整體效率比較高。
HashMap有對應的TreeMap,HashSet也有對應的TreeSet,下節,我們來看TreeSet。
---------------
未完待續,查看最新文章,敬請關注微信公眾號“老馬說編程”(掃描下方二維碼),從入門到高級,深入淺出,老馬和你一起探索Java編程及計算機技術的本質。用心原創,保留所有版權。
