背景
快速排序,是在上世紀60年代,由美國人東尼·霍爾提出的一種排序方法。這種排序方式,在當時已經是非常快的一種排序了。因此在命名上,才將之稱為“快速排序”。這個算法是二十世紀的七大算法之一,平均情況下時間復雜度為Ο(nlogn),而且在O(nlogn)的情況下,實際的運算速度都要快於其他同時間復雜度的排序方法。
對東尼·霍爾以及快速排序的提出背景感興趣的同學,可以看看這篇介紹:http://www.nowamagic.net/librarys/veda/detail/2391
排序思想
快速排序的思路想到很困難,但是理解起來卻非常容易
他的思路是這樣的:
1、先選定隊列中,某一個元素為基數Value(一般選擇頭元素,或尾元素)。
2、將基數Value依次與所有元素比較大小。按照比較結果將元素分為兩個隊列A、B。一個所有元素比基數Value大,一個所有元素比基數Value小。
3、將A作為新的隊列,再次選定基數,然後分成兩個更小的隊列
4、就這樣一直將每一個小的隊列無限的拆分成更小的兩個隊列。
5、一直到一個隊列已經拆分成不能拆封為止(也就是一個元素)
6、因為隊列之間的順序都是固定的。將這些隊列一次組合起來,整體的排序就算完成了。
(防盜連接:本文首發自http://www.cnblogs.com/jilodream/ )
注意這裡有兩個最核心的步驟,就是
1、選出Value元素,將整體隊列劃分成兩個子隊列
2、然後將子隊列重新作為一個新的,整體規模比當前要小的,新的隊列,進行計算,直到計算起來非常容易為止。
這兩個核心步驟造就了快排天生的優勢:
1、通過比較大小劃分到子隊列中的元素,在未來的比較過程中,這個元素的比較范圍始終都停留在這個子隊列中,不再做多余的比較。這使得早期的比較對後期的比較仍然有很大的影響。而類似於冒泡的排序方法,則前期很多的比較,對後期的作用非常小。這點和kmp算法很像,前期的比較盡量做到最大的利用。
2、將原有規模的隊列,拆分成若干個規模小的子隊列,這些子隊列要(防盜連接:本文首發自http://www.cnblogs.com/jilodream/ )解決的問題與原有隊列一致,只是規模變小了。這樣不斷的拆分,形成一種分而治之的思想。這種思想與背包算法也是不謀而合。
對於文字理解起來有困難的同學,可以看下下邊這張網上經典的動態圖,非常生動:
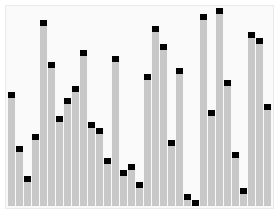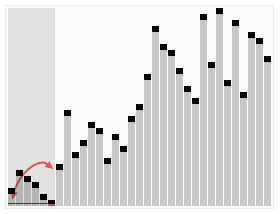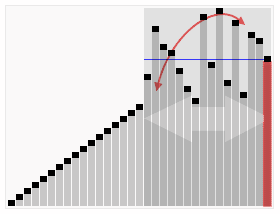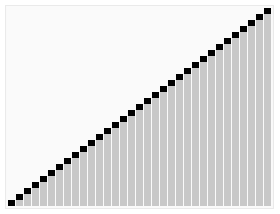
下邊是java實現的代碼
1 import java.util.Arrays;
2
3 public class QuickSort
4 {
5 public static void main(String args[])
6 {
7 QuickSort quicksort = new QuickSort();
8 int[] arrays = new int[]
9 { 1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 17, 17, 177, 18, 8, 8, 19 };
10 quicksort.quickSort(arrays);
11 System.out.println(Arrays.toString(arrays));
12 }
13
14 private void quickSort(int[] arrays)
15 {
16 subQuickSort(arrays, 0, arrays.length - 1);
17 }
18
19 private void subQuickSort(int[] arrays, int start, int end)
20 {
21 if (start >= end)
22 {
23 return;
24 }
25 int middleIndex = subQuickSortCore(arrays, start, end);
26 subQuickSort(arrays, start, middleIndex - 1);
27 subQuickSort(arrays, middleIndex + 1, end);
28 }
29
30 private int subQuickSortCore(int[] arrays, int start, int end)
31 {
32 int middleValue = arrays[start];
33 while (start < end)
34 {
35 while (arrays[end] >= middleValue && start < end)
36 {
37 end--;
38 }
39 arrays[start] = arrays[end];
40 while (arrays[start] <= middleValue && start < end)
41 {
42 start++;
43 }
44 arrays[end] = arrays[start];
45 }
46 arrays[start] = middleValue;
47 return start;
48 }
49 }