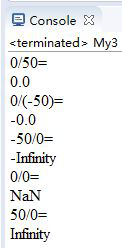一、原碼、反碼和補碼
(出處:http://www.cnblogs.com/zhangziqiu/ )
1、機器數和真值
在學習原碼, 反碼和補碼之前, 需要先了解機器數和真值的概念.
(1)、機器數
一個數在計算機中的二進制表示形式, 叫做這個數的機器數。機器數是帶符號的,在計算機用一個數的最高位存放符號, 正數為0, 負數為1.比如,十進制中的數 +3 ,計算機字長為8位,轉換成二進制就是00000011。如果是 -3 ,就是 10000011 。那麼,這裡的 00000011 和 10000011 就是機器數。
(2)、真值
因為第一位是符號位,所以機器數的形式值就不等於真正的數值。例如上面的有符號數 10000011,其最高位1代表負,其真正數值是 -3 而不是形式值131(10000011轉換成十進制等於131)。所以,為區別起見,將帶符號位的機器數對應的真正數值稱為機器數的真值。例:0000 0001的真值 = +000 0001 = +1,1000 0001的真值=–000 0001 =–1
2、原碼
原碼就是符號位加上真值的絕對值, 即用第一位表示符號, 其余位表示值. 比如如果是8位二進制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符號位. 因為第一位是符號位, 所以8位二進制數的取值范圍就是:
[1111 1111 , 0111 1111]
即[-127 , 127]
原碼是人腦最容易理解和計算的表示方式.
3、反碼
反碼的表示方法是:
正數的反碼是其本身
負數的反碼是在其原碼的基礎上, 符號位不變,其余各個位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可見如果一個反碼表示的是負數, 人腦無法直觀的看出來它的數值. 通常要將其轉換成原碼再計算.
4、補碼
補碼的表示方法是:
正數的補碼就是其本身
負數的補碼是在其原碼的基礎上, 符號位不變, 其余各位取反, 最後+1. (即在反碼的基礎上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]補
[-1] = [10000001]原 = [11111110]反 = [11111111]補
對於負數, 補碼表示方式也是人腦無法直觀看出其數值的. 通常也需要轉換成原碼在計算其數值.
5、Java對正負數進行各種位操作使用的是補碼
現在我們知道了計算機可以有三種編碼方式表示一個數. 對於正數因為三種編碼方式的結果都相同:
[+1] = [00000001]原 = [00000001]反 = [00000001]補
所以不需要過多解釋. 但是對於負數:
[-1] = [10000001]原 = [11111110]反 = [11111111]補
可見原碼, 反碼和補碼是完全不同的. 既然原碼才是被人腦直接識別並用於計算表示方式, 為何還會有反碼和補碼呢?
首先, 因為人腦可以知道第一位是符號位, 在計算的時候我們會根據符號位, 選擇對真值區域的加減. (真值的概念在本文最開頭). 但是對於計算機, 加減乘數已經是最基礎的運算, 要設計的盡量簡單. 計算機辨別"符號位"顯然會讓計算機的基礎電路設計變得十分復雜! 於是人們想出了將符號位也參與運算的方法. 我們知道, 根據運算法則減去一個正數等於加上一個負數, 即: 1-1 = 1 + (-1) = 0 , 所以機器可以只有加法而沒有減法, 這樣計算機運算的設計就更簡單了.於是人們開始探索 將符號位參與運算, 並且只保留加法的方法. 首先來看原碼:
計算十進制的表達式: 1-1=0
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
如果用原碼表示, 讓符號位也參與計算, 顯然對於減法來說, 結果是不正確的.這也就是為何計算機內部不使用原碼表示一個數.
為了解決原碼做減法的問題, 出現了反碼:
計算十進制的表達式: 1-1=0
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
發現用反碼計算減法, 結果的真值部分是正確的. 而唯一的問題其實就出現在"0"這個特殊的數值上. 雖然人們理解上+0和-0是一樣的, 但是0帶符號是沒有任何意義的. 而且會有[0000 0000]原和[1000 0000]原兩個編碼表示0.
於是補碼的出現, 解決了0的符號以及兩個編碼的問題:
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]補 + [1111 1111]補 = [0000 0000]補=[0000 0000]原
這樣0用[0000 0000]表示, 而以前出現問題的-0則不存在了.而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]補 + [1000 0001]補 = [1000 0000]補
-1-127的結果應該是-128, 在用補碼運算的結果中, [1000 0000]補 就是-128. 但是注意因為實際上是使用以前的-0的補碼來表示-128, 所以-128並沒有原碼和反碼表示.(對-128的補碼表示[1000 0000]補算出來的原碼是[0000 0000]原, 這是不正確的)
使用補碼, 不僅僅修復了0的符號以及存在兩個編碼的問題, 而且還能夠多表示一個最低數. 這就是為什麼8位二進制, 使用原碼或反碼表示的范圍為[-127, +127], 而使用補碼表示的范圍為[-128, 127].
因為機器使用補碼, 所以對於編程中常用到的32位int類型, 可以表示范圍是: [-231, 231-1] 因為第一位表示的是符號位.而使用補碼表示時又可以多保存一個最小值.
二、仔細閱讀示例: EnumTest.java,運行它,分析運行結果?
你能得到什麼結論?
1、源程序:
package demo;
public class EnumTest {
public static void main(String[] args) {
Size s=Size.SMALL;
Size t=Size.LARGE;
//s和t引用同一個對象?
System.out.println(s==t);
//是原始數據類型嗎?
System.out.println(s.getClass().isPrimitive());
//從字符串中轉換
Size u=Size.valueOf("SMALL");
System.out.println(s==u); // //列出它的所有值
for(Size value:Size.values()){
System.out.println(value);
}
}
}
enum Size{SMALL,MEDIUM,LARGE};
2、結果:
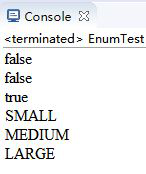
3、結果分析:枚舉類型的表示方法:enum Size{ SMALL , MEDIUM , LARGE }
使用方法:Size s=Size.SMALL;
//從字串轉換為枚舉
Size t=Size.valueof(“SMALL”);
枚舉類型是引用類型,枚舉不屬於原始數據類型,它的每個具體值都引用一個特定的對象。相同的值則引用同一個對象。可以使用“==”和equals()方法直接比對枚舉變量的值,換句話說,對於枚舉類型的變量,“==”和equals()方法執行的結果是等價的。當判斷兩個賦值是否相同時,輸出結果只能是ture或false。當輸出value時,需要Size value:Size.values()循環類型的數量的次數。enum Size{SMALL,MEDIUM,LARGE};語句可以寫在程序的最後,也可以寫在前面,但必須自己引用。枚舉的賦值可以有兩種表示方法:1.Size s=Size.SMALL; 2.Size t=Size.valueof(“SMALL”)。
三、 Java變量遵循“同名變量的屏蔽原則”,請課後閱讀相關資料弄清楚相關知識,然後自己編寫一些測試代碼,就象本示例一樣,有意識地在不同地方定義一些同名變量,看看輸出的到底是哪個值。
1、源程序:
package demo;
public class My1 {
private static int value=1;
public static void main(String[] args){
int value=2;
System.out.println(value);
}
}
結果:2
2、源程序:
package demo;
public class My1 {
private static int value=10;
public static void main(String[] args){
int value=6;
System.out.println(value);
}
}
結果:6
3、結論:在函數裡面的賦值優先於在函數外賦值,屬於局部變量。函數外的賦值可以賦給類中的多個函數,屬於全局變量。如果函數裡面沒有重復的賦值,那麼函數的值為函數外的。
四、看著這個圖,再查查Java中每個數據類型所占的位數,和表示數值的范圍,你能得出什麼結論?
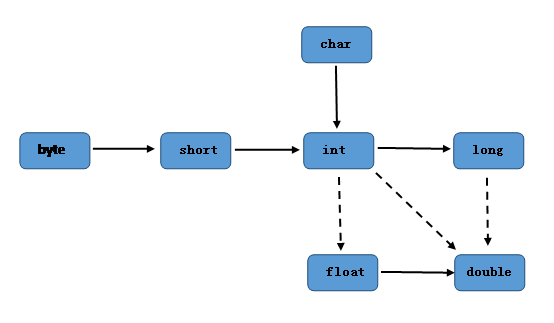
答:自動類型轉換是安全的,強制類型轉換時,可能會引起信息的損失。實線代表無精度損失,虛線代表有精度損失,一般來說在實線兩端都是由低精度指向高精度的類型,所占的位數從低到高,范圍從小到大,所以可得出,低精度向高精度轉化不丟失精度,反之,從高精度傳向低精度則會損失。
五、請運行以下代碼(TestDouble.java),你看到了什麼樣的輸出,意外嗎?

答:結果為
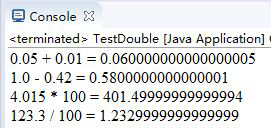
感到意外,使用double類型的數值進行計算, 其結果是不精確的。計算機只能識別二進制,一切的數據最後都要轉換為二進制。例如源程序中的0.05是十進制的,要轉換為二進制,但0.05的二進制不是精確的0.05,只是接近0.05,實際為0.04999 999 999 999 999,浮點數由兩部分組成:指數和尾數,再進行浮點數的二進制與十進制的轉換時,浮點數參與了計算,那麼轉換過程就變的不可預測,並且變得不可逆。
六、在構建BigDecimal對象時應使用字符串而不是double數值,否則,仍有可能引發計算精度問題。(為什麼會這樣呢?)
package demo;
import java.math.BigDecimal;
public class TestBigDecimal
{
public static void main(String[] args)
{
BigDecimal f1 = new BigDecimal("0.05");
BigDecimal f2 = BigDecimal.valueOf(0.01);
BigDecimal f3 = new BigDecimal(0.05);
System.out.println("下面使用String作為BigDecimal構造器參數的計算結果:");
System.out.println("0.05 + 0.01 = " + f1.add(f2));
System.out.println("0.05 - 0.01 = " + f1.subtract(f2));
System.out.println("0.05 * 0.01 = " + f1.multiply(f2));
System.out.println("0.05 / 0.01 = " + f1.divide(f2));
System.out.println("下面使用double作為BigDecimal構造器參數的計算結果:");
System.out.println("0.05 + 0.01 = " + f3.add(f2));
System.out.println("0.05 - 0.01 = " + f3.subtract(f2));
System.out.println("0.05 * 0.01 = " + f3.multiply(f2));
System.out.println("0.05 / 0.01 = " + f3.divide(f2));
}
}
答:結果為
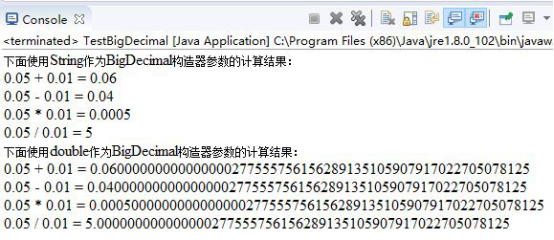
由此可見,構建BigDecimal對象可以解決不精確的問題。但是使用時應使用字符串而不是double數值,否則,仍有可能引發計算精度問題。
七、以下代碼的輸出結果是什麼?
int X=100;
int Y=200;
System.out.println("X+Y="+X+Y);
System.out.println(X+Y+"=X+Y");
為什麼會有這樣的輸出結果?
答:源程序:
package demo;
public class Youxi {
public static void main(String[] args){
int X=100;
int Y=200;
System.out.println("X+Y="+X+Y);
System.out.println(X+Y+"=X+Y");
}
}
結果:
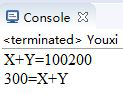
在System.out.println()中,如果在string字符串後面是+和變量,會把變量轉換成string類型,加號起連接作用,然後把兩個字符串連接成一個新的字符串輸出;如果先有變量的加減運算再有字符串,那麼會從左到右先計算變量的加減,然後再與後面的string結合成一個新的字符串。也就是說加號只有在兩個string類型或者其中一個是string類型的時候才起到連接作用,否則仍然是運算符。
八、Java中出現0的情況
答:0.0/0.0 得到的結果是NaN(not an number的簡稱,即"不是數字")。通過Double.isNaN(double x)來判斷。
正數/0.0 得到的結果是正無窮大,即Infenity
負數/0.0 得到的結果是負無窮大,即Infenity。通過Double.isInfinite(double x)來判斷。
源程序:
package demo;
public class My3{
public static void main(String[] args) {
double a=0,
b=50,
c=-50;
System.out.println("0/50= \n"+(a/b));
System.out.println("0/(-50)= \n"+(a/c));
System.out.println("-50/0= \n"+(c/a));
System.out.println("0/0= \n"+(a/a));
System.out.println("50/0= \n"+(b/a));
}
}
結果: