(-1)寫在前面
在一次面試中被問及快速排序,回來後又看了一次以前做過的案例,說來慚愧,時至今日還需要讀好長時間,才能明白自己代碼的意思,主要是缺少注釋和圖解,深有感慨,決定好好記錄一下。
之所以使用二叉樹,是因為用遞歸實現當數據量過大時會報棧溢出的錯誤,我試了一下別人的電腦也是這個問題。當然使用二叉樹也會報內存不足,原因是無法創建那麼長的數組,堆區內存溢出。個人感覺要比遞歸實現好的多。
(0)算法詳解
程序隨機產生數據,將其放在數組裡。
a.將最小索引到最大索引之間的數據看做一個整體,程序已最小索引代表的數A為准
b.調換A的位置,使得A左邊是比A大的數,A右邊是比A小的數,此時A的索引被稱為中間索引
c.最小索引到 中間索引-1被看為左孩子 ,中間索引+1 到最大索引被看做右孩子
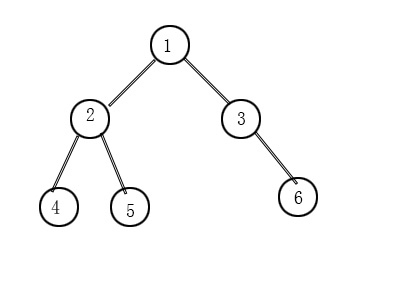
已此圖為例,說明程序流程:
每個節點代表一個數組片段,1是根節點,代表整個數組,每個片段都要經歷a、b的操作
順序為操作1,創建2,3,操作2,創建4,5,操作4,回到2,操作5,回到2,回到1,操作3,創建6,操作6,回到3,回到1,完事。
以下面這個數組為例,說明程序流程
int[] oop = {510, 107,948, 659, 955,438, 283,822};
第一次
a 步驟 最小索引0,最大索引7 A –>510
b步驟 [822, 955, 948, 659, 510, 438, 283, 107]
c 步驟 左孩子0-3 右孩子5-7
第二次
a 步驟 最小索引0,最大索引3 A –>822
b步驟 [948, 955, 822,659]
c 步驟 左孩子0-1 右孩子沒有
第三次
a 步驟 最小索引0,最大索引1 A –>948
b步驟 [955, 948]
c 步驟 左孩子沒有、 右孩子沒有
第四次
a 步驟 最小索引5,最大索引7 A –>438
b步驟[438, 283, 107]
c 步驟 左孩子沒有、, 右孩子6-7
第五次
a 步驟 最小索引6,最大索引7 A –>283
b步驟[283, 107]
c 步驟 左孩子沒有、 右孩子沒有
(2)具體實現
class Test
{
public static void main(String[] args)
{
int len = 8000000;
int[] oop = new int[len];
for(int i=0;i<len;i++)
oop[i] = (int)(Math.random()*1000);
Calendar c1 = Calendar.getInstance();
Sort.quick_sort(oop);
Calendar c2 = Calendar.getInstance();
System.out.println(c2.getTimeInMillis()-c1.getTimeInMillis());
}
}
class Binary
{
private int left,//最小索引
right;//最大索引
private Binary beforeBinary,//父節點
rightBinary,//左孩子
leftBinary;//右孩子
public Binary(int left,int right)
{
this.left= left;
this.right = right;
}
public void setLeft(int left)
{
this.left = left;
}
public void setRight(int right)
{
this.right = right;
}
public void setBefore(Binary beforeBinary)
{
this.beforeBinary = beforeBinary;
}
public void setRightBinary(Binary rightBinary)
{
this.rightBinary = rightBinary;
}
public void setLeftBinary(Binary leftBinary)
{
this.leftBinary = leftBinary;
}
public int getLeft()
{
return this.left;
}
public int getRight()
{
return this.right;
}
public Binary getBeforeBinary()
{
return this.beforeBinary;
}
public Binary getRightBinary()
{
return this.rightBinary;
}
public Binary getLeftBinary()
{
return this.leftBinary;
}
}
class Sort
{
public static void quick_sort(int[] oop)
{
Binary headBinary = new Binary(0,oop.length-1),
tempBinary = headBinary;
int right,
left,
tempNumber;
boolean flag = true;
headBinary.setBefore(null);
do
{
left = tempBinary.getLeft();
right = tempBinary.getRight();
tempNumber = oop[left];
while(left<right)//結束循環後,tempNumber的左邊是比他大的數,tempNumber的右邊是比他小的數
{
while(left<right && tempNumber>=oop[right])//從右邊找到比tempNumber大的數
right--;
if(left<right)
{
oop[left] = oop[right];//將右邊的數賦值給左邊的
left++;//縮減范圍
}
while(left<right && tempNumber<=oop[left])//從左邊開始找比tempNumber小的數
left++;
if(left<right)
{
oop[right] = oop[left];//將左邊的數賦值給右邊
right--;//縮減范圍
}
}
//此時left==right
oop[left] = tempNumber;
if(right<tempBinary.getRight()-1)//創建左孩子
{
Binary c1 = new Binary(right+1,tempBinary.getRight());
tempBinary.setRightBinary(c1);
c1.setBefore(tempBinary);
}
if(left-1>tempBinary.getLeft()) //創建右孩子
{
Binary c1 = new Binary(tempBinary.getLeft(),left-1);
tempBinary.setLeftBinary(c1);
c1.setBefore(tempBinary);
}
flag = true;
do//操作A:(遍歷左孩子、右孩子,如果左孩子、右孩子都被遍歷,返回上次節點)重復A操作,直到遍歷到跟節點
{
if(tempBinary.getLeftBinary() != null)//如果左孩子被創建了,就先遍歷左孩子
{
Binary c1 = tempBinary.getLeftBinary();;
tempBinary.setLeftBinary(null);//最為重要,只要被遍歷的左孩子就將起在上層節點的引用設為null,
tempBinary = c1;
flag = false;
}
else if(tempBinary.getRightBinary() != null)//右孩子總是左兄弟節點遍歷後才被遍歷
{
Binary c1 = tempBinary.getRightBinary();
tempBinary.setRightBinary(null);
tempBinary = c1;
flag = false;
}
else //左孩子。右孩子都被遍歷返回父節點
{
if(tempBinary == headBinary) break;
tempBinary = tempBinary.getBeforeBinary();
}
}while(flag);
}while(tempBinary != headBinary);//當回溯到根節點時,說明排序完畢
}
}
(3)簡單測試
80000000 內存溢出
8000000 66607ms
800000 1027ms