插入排序和希爾排序

插入排序和希爾排序

插入排序：

插入排序由n-1趟排序組成。第 i 趟排序前，保證從位置 0 到位置i-1 上的元素已經是排序狀態（這是插入排序正確的原因，也是前提條件）。

所以第 i 趟的排序工作就是將 A[i] 放到 A[0,1,2,3...i-1]中的正確的位置。

舉個例子。就像玩撲克牌的時候，我們每次拿到的是一張不知道的牌，然後順著左手中已經有的牌遍歷，然後找到它正確的位置後插入這張新牌，這時候在這新插入的牌之前的牌的位置是不變的。但它之後的牌的位置都向後依次移動了一位。

我們給個簡單的圖例：

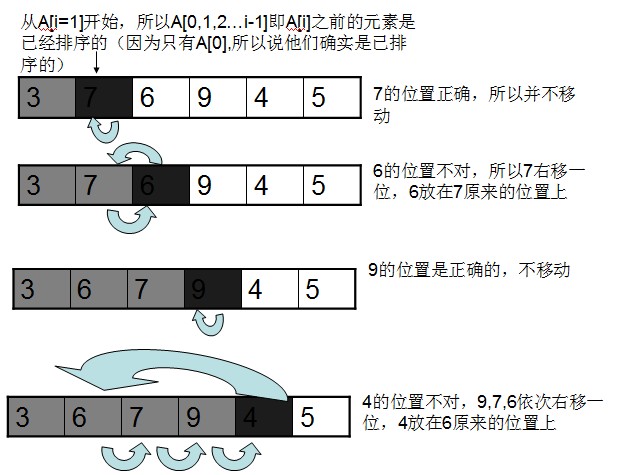
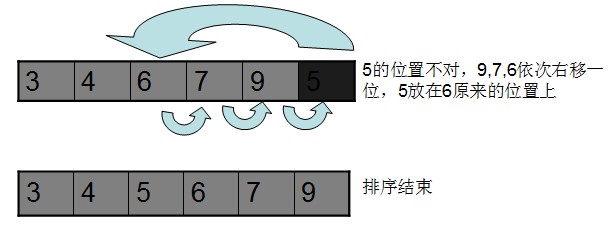
代碼如下

void InsertSort(int *A,int n)
{
int i,j;
int key;
for(i=1;i
{
key=A[i];

/*檢測是不是在正確的位置上*/
for(j=i;j>0&&key
A[j]=A[j-1];

A[j]=key;
}
}

基於上面的解釋，插入排序應該很好理解了。下面我們來分析一下插入排序的運行時間問題。

最壞情況下，當輸入的逆序的。內層循環每次都執行，且執行最大次數。

所以 T(n)=2+3+4+....n=O(n^2);

最好情況下，當輸入是已排序時，內層循環並不工作

所以時間復雜度T(n)=O(n)

所以插入排序的運行時間變化差別是很大的，如果輸入幾乎被排序，那麼插入排序的運行時間很快。

對於平均時間的分析，我們假設不存在重復的元素。

我們先來討論一下插入排序到底做了什麼事情。

我們定義一個逆序：i < j 但 A[i]>A[j] 這樣的一個序偶（A[i],A[j]）我們稱為一個逆序，

所以顯然插入排序所做的工作就是同交換相鄰元素來消除逆序對，從而帶到排序的目的。所以插入排序的運行時間可表示為 T(n)=O(I+n)。其中 I 為逆序數，O(n)為所做的其他線性工作。

那麼如果我們知道一個任意輸入序列中的平均逆序數，就知道了插入排序的平均運行時間。

定理：含N個互異數的數組的平均逆序數是N(N-1)/4

證明如下：

考慮一個序列 A ,和它的反序列 A~ 。則任意一個序偶（a,b）必定是A或者A~中的一個逆序數

比如序列A=3,6,1,4,8,7,9和它的反序列A~=9,7,8,4,1,6,3 則（3,6）是A~中的一個逆序 （4,6）是A中的一個逆序。

所以對於n個元素的序列A，任意取兩個數組成的序偶。必定是A和A~中的一個逆序

所以總的序偶數為 N(N-1)/2 （這是相對於A和A~整體而言。）

所以 A 中的逆序數為總逆序數的一半 即N(N-1)/4.

我們看到任意不包含相同元素的數組A的逆序數為 O(n^2)

所以我們得到差投入排序的平均時間為T(n)=O(n^2).

希爾排序：

我們將希爾排序和插入排序在一起介紹，原因就是希爾排序的原理和插入排序是一樣的，只是它多了一個增量序列。

他也是通過比較元素來工作，不同的是它並不像插入排序那樣比較相鄰的元素，而是比較相距一定距離的元素。各躺比較所用的距離也逐漸減小，直到距離減小為1。

所以他的最後一次進行的就是插入排序。

希爾排序使用的的增量序列H1,H2,H3````Hk.只要h1=1 任何增量序列都是可行的。但存在一些序列比另外一些序列更好。

使用增量Hi排序依次後，對於每一個i 有A[i]<=A[i+Hi] 即所有相距Hi的元素都被排序了 。此時稱數組是Hi 排序的。並且在之後的排序中保持它的Hi 排序性。

我們給出其代碼。我們使用Shell建議的增量序列Hi=N/2和Hi=Hi/2.

void ShellSort(int *A,int n)
{
int i,j;
int increase;
int key;
for(increase=n/2;increase>0;increase/=2)
  {
for(i=1;i
{
key=A[i];
for(j=i;j>0&&j-increase>=0;j-=increase)
{
if(key
A[j]=A[j-increase];
else
break;
}
A[j]=key;
}
}
}

對於希爾排序的運行時間分析通常基於特定的增量序

對於希爾增量 T(n)=O(n)

對Hibbard（1,3,7。。。。2k-1）增量T(n)=O(N^3/2) (k和3/2為指數)。

對Sedgewick（1,5,19,41,109.。。。）增量T(n)=O(N^7/6) (7/6為指數)。

對於他們的定量分析參考《數據結構與算法分析》P169