二叉樹鏈式存儲和遍歷，二叉樹鏈式存儲

二叉樹鏈式存儲和遍歷，二叉樹鏈式存儲

1 二叉樹的鏈式存儲

1.1 鏈式存儲

      順序存儲對空間利用率較低，所以，二叉樹一般采用鏈式存儲結構，用一個鏈表來存儲一顆二叉樹。二叉鏈表至少包含3個域：數據域data，左指針域lchild和右指針域rchild，如果再加上一個指向雙親結點的指針就變成了三叉鏈表。

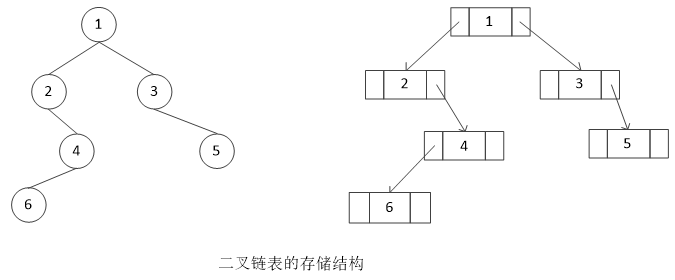
二叉樹的鏈式存儲結構如下：

/**
 * 二叉鏈表結點
 * @author cyhe
 */
private class Node{
    Integer data;
    Node lchild, rchild;
}

      根據完全二叉樹的序列遞歸創建二叉樹，輸入序列時不存在的結點用0代替，以下是創建的代碼和一些有用的方法。

/**
 * 存儲先序輸入的二叉樹，默認大小為10，當超過10自動調用resize方法擴容
 */
private Integer[] nodes = new Integer[10];
public LinkBiTree(){
    init();
}
/**
 * 獲取根節點
 * @return
 */
public Node getRoot(){
    return root;
}
/**
 * 滿了自動擴容
 * @param max
 */
private void resize(int max){
    Integer[] temp = new Integer[max];
    for(int i=0; i<nodes.length; i++){
        temp[i] = nodes[i];
    }
    nodes = temp;
}
/**
 * 先序輸入二叉樹，不存在的結點使用0
 */
public void init(){
    System.out.println("先序列輸入一個二叉樹，不存在的結點用0代替，使用逗號隔開：");
//        String[] ins = StdIn.readString().split(",");
    String[] ins = "1,2,3,4,0,5,7,8".split(",");
    n = ins.length;
    for (int i = 0; i < ins.length; i++) {
        if(i>=nodes.length){
            resize(2 * nodes.length); // 擴大兩倍
        }
        nodes[i] = Integer.valueOf(ins[i]);
    }
    System.out.println("LinkBiTree [nodes=" + Arrays.toString(nodes) + "]");
    root = build(1); // 遞歸創建樹
    System.out.println("輸入的樹高度為："+depth(root));
    print();
}
/**
 * 遞歸創建一顆樹, 使用完全二叉樹序列
 * @param node
 * @param data
 */
public Node build(int index){
    if (index > n) {
        return null;
    }
    Integer tmp = nodes[index - 1]; // 獲取結點的值
    if (tmp == 0) { // 若為 0 表示結點不存在
        return null;
    } else {
        Node node = new Node();
        node.data = tmp;
        node.lchild = build(2 * index); // 創建左子樹
        node.rchild = build(2 * index + 1); // 創建右子樹
        return node;
    }
}
/**
 * 遞歸獲取二叉樹的高度
 * @return
 */
public int depth(Node node){
    if(node != null){
        int l = depth(node.lchild); // 左子樹高度
        int r = depth(node.rchild); // 右子樹高度
        return l > r ? l + 1 : r + 1; // 樹的高度為子樹最大高度加上根節點
    }
    return 0; // 空樹高度為0
}

1.2 層次遍歷

/**
 * 層次遍歷，利用隊列是實現
 */
public void levelOrder(Node root){
    RingBuffer<Node> queue = new RingBuffer<Node>(n+1);
    queue.put(root); // 根節點先進隊列
    
    while(queue.size()>0){
        Node tmp = queue.get();
        System.out.print(tmp.data + " "); // 根

        if (tmp.lchild != null) { // 如果根節點的左子樹存在，把左子樹編號入棧
            queue.put(tmp.lchild);
        }
        
        if (tmp.rchild != null) { // 如果根節點的右子樹存在，把右子樹編號入棧
            queue.put(tmp.rchild);
        }
    }
}

1.3 先序遍歷

1.3.1 遞歸實現

/**
 * 遞歸先序遍歷
 */
public void preOrderRecur(Node node){
    if(node != null){
        System.out.print(node.data+" "); // 根
        preOrderRecur(node.lchild); // 左
        preOrderRecur(node.rchild); // 右
    }
}

1.3.2 非遞歸實現

實現方法1：

/**
 * 非遞歸先序遍歷
 */
public void preOrder(Node node){
    ArrayStack<Node> stack = new ArrayStack<Node>(n + 1);
    stack.push(node);
    while (!stack.isEmpty()) {
        Node tmp = stack.pop();
        System.out.print(tmp.data + " "); // 根

        if (tmp.rchild != null) { // 如果根節點的右子樹存在，把右子樹編號入棧
            stack.push(tmp.rchild);
        }
        if (tmp.lchild != null) { // 如果根節點的左子樹存在，把左子樹編號入棧
            stack.push(tmp.lchild);
        }
    }
}

實現方法2:

/**
 * 非遞歸先序遍歷
 */
public void preOrderOne(Node node){
    ArrayStack<Node> stack = new ArrayStack<Node>(n + 1);
    while (node != null || !stack.isEmpty()) {
        while(node != null){ // 把最左側的全部入棧
            System.out.print(node.data + " "); // 根
            stack.push(node);
            node = node.lchild;
        }
        Node tmp = stack.pop(); // 彈出最後入棧的左子樹
        node = tmp.rchild; // 看它有沒有右孩子
    }
}

1.4 中序遍歷

1.4.1 遞歸實現

/**
 * 遞歸中序遍歷
 */
public void inOrderRecur(Node node){
    if(node != null){
        inOrderRecur(node.lchild); // 左
        System.out.print(node.data+" "); // 根
        inOrderRecur(node.rchild); // 右
    }
}

1.4.2 非遞歸實現

/**
 * 非遞歸中序遍歷
 */
public void inOrder(Node node){
    ArrayStack<Node> stack = new ArrayStack<Node>(n + 1);
    while (node != null || !stack.isEmpty()) {
        while(node != null){ // 把最左側的全部入棧
            stack.push(node);
            node = node.lchild;
        }
        Node tmp = stack.pop(); // 彈出最後入棧的左子樹
        System.out.print(tmp.data + " "); // 先訪問左子樹
        node = tmp.rchild; // 看它有沒有右孩子
    }
}

1.5 後序遍歷

1.5.1 遞歸實現

/**
 * 遞歸後序遍歷
 */
public void postOrderRecur(Node node){
    if(node != null){
        postOrderRecur(node.lchild); // 左
        postOrderRecur(node.rchild); // 右
        System.out.print(node.data+" "); // 根
    }
}

1.5.2 非遞歸實現

/**
 * 非遞歸後序遍歷
 */
public void postOrder(Node node){
    ArrayStack<Node> stack = new ArrayStack<Node>(n + 1);
    Node pre = null; // 前一個訪問的結點
    while (node != null || !stack.isEmpty()) {
        while(node != null){ // 把最左側的全部入棧
            stack.push(node);
            node = node.lchild;
        }
        Node tmp = stack.peek(); // 現在要判斷棧內結點有沒有右孩子，或者右孩子是否訪問過
        
        // 如果當前結點不存在右孩子或者右孩子已經訪問過，則訪問當前結點
        if(tmp.rchild == null || pre == tmp.rchild){
            Node n = stack.pop();
            System.out.print(n.data + " "); // 訪問結點
            pre = n;
        } else {
            node = tmp.rchild; // 否則訪問右孩子
        }
    }
}

2 測試

public static void main(String[] args) {
    LinkBiTree<Integer> biTree = new LinkBiTree<Integer>();
    
    System.out.print("先序遍歷(遞歸)：");
    biTree.preOrderRecur(biTree.getRoot());
    System.out.print("\n中序遍歷(遞歸)：");
    biTree.inOrderRecur(biTree.getRoot());
    System.out.print("\n後序遍歷(遞歸)：");
    biTree.postOrderRecur(biTree.getRoot());
    System.out.print("\n層次遍歷：");
    biTree.levelOrder(biTree.getRoot());
    System.out.print("\n先序遍歷(非遞歸)：");
//    biTree.preOrder(biTree.getRoot());
    biTree.preOrderOne(biTree.getRoot());
    System.out.print("\n中序遍歷(非遞歸)：");
    biTree.inOrder(biTree.getRoot());
    System.out.print("\n後序遍歷(非遞歸)：");
    biTree.postOrder(biTree.getRoot());
}

2.1 輸出結果