問題描述:假設表達有兩種符號:圓的和方的,嵌套的順序任意,判斷嵌套是否正確,如 ([]()) 或 [[()]]均為正確,而 [(]) 或 (()] 均為不正確。
算法描述:
(1)初始化一個空棧,順序讀入括號;
(2)若是左括號直接進棧;
(3)若是右括號,先出棧一個元素比較是否與其匹配,如匹配則繼續比較下一個括號,若不匹配則返回匹配失敗;
(4)最後若棧不為空,說明還有沒匹配的括號,匹配失敗,否則匹配成功。
/**
* 檢查括號是否匹配
* @param match 待匹配字符串
* @return true 匹配成功,false 匹配失敗
*/
public static boolean isMatching(String match){
char[] braces = match.trim().toCharArray();
for(char ch : braces){
if(ch == '[' || ch == '('){
stack.push(ch);
} else if(ch == ']'){
char t = stack.pop();
if('[' == t){
continue;
} else {
return false;
}
} else if(ch == ')'){
char c = stack.pop();
if('(' == c){
continue;
} else {
return false;
}
}
}
if(stack.size() > 0){
return false;
} else {
return true;
}
}
算術表達式由括號、運算符和操作數組成,表達式求值的關鍵在於如何解析字符串,並按照正確的順序完成運算。表達式有中綴表達式,不僅要考慮運算符優先級,還要考慮括號,後綴表達式已經考慮了優先級,只有操作數和運算符,在此提供兩種方案解決表達式求值。
首先定義運算符優先級,運算符只存在兩個位置,棧內和棧外,優先級也分為棧內優先級(in stack priority)和棧外優先級(in comming priority),棧的特性是後進先出,棧外的運算符優先級大,則入棧它迫切先計算,對於相同級別的運算符,棧內的優先級大於棧外的優先級,則出棧。據此設計運算符優先級表:(用isp,icp分別表示棧內和棧外優先級,#號表示字符串結束)
表1 運算符優先級表
操作符
#
(
+,-
*,/
)
isp
0
1
3
5
6
icp
0
6
2
4
1
在Java中使用兩個HashMap存儲棧內和棧外運算符優先級,代碼如下:
static ArrayStack<String> ops = new ArrayStack<String>(10); // 運算符棧
static ArrayStack<Double> vals = new ArrayStack<Double>(20); // 操作數棧
static String opstr = "(+-*/)"; // 涉及到的運算符
static Map<String, Integer> isp = new HashMap<String, Integer>(); // 棧內優先級
static Map<String, Integer> icp = new HashMap<String, Integer>(); // 棧外優先級
static{
isp.put("#", 0);isp.put("(", 1); isp.put("+", 3); isp.put("-", 3); isp.put("*", 5); isp.put("/", 5); isp.put(")", 6);
icp.put("#", 0);icp.put("(", 6); icp.put("+", 2); icp.put("-", 2); icp.put("*", 4); icp.put("/", 4); icp.put(")", 1);
}
1.2.1 直接使用中綴表達式求值
算法描述:
(1)初始化兩個棧,操作數棧和運算符棧,順序讀取字符串
(2)如果是操作數直接入操作數棧;
(3)如果是運算符,如果當前運算符優先級大於運算符棧頂優先級,則直接入運算符棧,如果小於則循環彈出一個操作符,兩個操作數計算,並將結果壓入操作數 棧,直到找到運算符優先級比它小的,最後如果當前運算符是右括號,則彈出一個運算符(彈出的是左括號),否則入運算符棧;
(4)如果字符為#說明已經到表達式末尾,則循環彈出操作符棧中的運算符及操作數計算,直到運算符棧為空,最後操作數棧中的元素即為結果。
/**
* 中綴表達式計算
*/
public static double infix(String expr){
ops.push("#");
char[] chs = expr.trim().toCharArray();
for(char ch : chs) {
String op = String.valueOf(ch);
// 如果是# 表示表達式結尾,把棧中的運算符全部彈出
if("#".equals(op)){
while(ops.size() > 0 && !"#".equals(ops.peek())){
vals.push(calculate(vals.pop(), vals.pop(), ops.pop().charAt(0)));
}
} else if(!opstr.contains(op)){// 如果是操作數,直接輸出
vals.push(Double.valueOf(op));
} else { // 運算符
// 當前運算符大於棧頂運算符優先級,則直接入操作符棧
if(icp.get(op) > isp.get(ops.peek())){
ops.push(op);
} else {
// 如果小於,循環出棧找到比它優先級小的,彈出一個操作符,兩個操作數,計算結果置入操作數棧
// 如果是 右括號) 即是匹配棧內的左括號),最後彈出),(不入棧
// 如果不是右括號,最後把這個運算符壓入運算符棧
while(icp.get(op) < isp.get(ops.peek())){
vals.push(calculate(vals.pop(), vals.pop(), ops.pop().charAt(0)));
}
if(!")".equals(op)){
ops.push(op);
} else {
ops.pop(); //彈出 ( 左括號
}
}
}
}
return vals.pop();
}
1.2.2 使用後綴表達式求值
後綴表達式已經包含了操作數以及運算符優先級,計算比較方便,遇操作數直接入棧,遇運算符彈出兩個操作數計算後再入棧,如此循環,最後操作數棧內即為結果。關鍵在於如何把中綴表達式轉為後綴表達式。
中綴表達式轉後綴表達式,算法描述:
(1)初始化一個運算符棧,順序讀取表達式字符串
(2)如果字符是操作數直接輸出
(3)如果字符是運算符,如果當前運算符優先級大於運算符棧頂優先級,則直接入運算符棧,如果小於則循環彈出一個操作符,直到找到運算符優先級比它小的,最 後如果當前運算符是右括號,則彈出一個運算符(彈出的是左括號),否則入運算符棧;
(4)若字符為# 表示已經到末尾,循環彈出運算符棧中的元素,直到棧空,最後的輸出即為中綴表達式。
/**
* 中綴表達式轉後綴
* @param expr
*/
public static String infix2suffix(String expr){
ops.push("#");
StringBuffer sb = new StringBuffer();
char[] chs = expr.trim().toCharArray();
for(char ch : chs){
String op = String.valueOf(ch);
// 如果是# 表示表達式結尾,把棧中的運算符全部彈出
if("#".equals(op)){
while(ops.size() > 0 && !"#".equals(ops.peek())){
sb.append(ops.pop());
}
} else if(!opstr.contains(op)){// 如果是操作數,直接輸出
sb.append(op);
} else { // 運算符
// 如果當前運算符優先級大於棧頂運算符優先級,則入棧
if(icp.get(op) > isp.get(ops.peek())) {
ops.push(op);
continue;
}
// 如果小於,彈出一個操作符,循環出棧直到比它優先級小
// 如果是 右括號) 即是匹配棧內的左括號),最後彈出),(不入棧
// 如果不是右括號,最後把這個運算符壓入運算符棧
while(icp.get(op) < isp.get(ops.peek())){
sb.append(ops.pop());
}
if(!")".equals(op)){
ops.push(op);
} else {
ops.pop(); //彈出 ( 左括號
}
}
}
return sb.toString();
}
所謂遞歸,就是函數調用了自己,以斐波那契數列為例,其定義為:
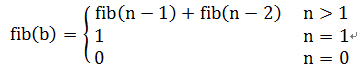
這是一個典型的遞歸例子,Java程序實現如下:
public static int Fib(int n){
if(n == 0){
return 0;
} else if(n == 1){
return 1;
} else {
return Fib(n-1) + Fib(n-2);
}
}
遞歸的效率不高,由於其中重復包含很多重復的計算。每個線程執行時,都有各自的棧,我們在debug時可以看到,在遞歸調用時,遞歸期間的數據都是保存在這個棧中,系統幫我們維護這個棧。
通常情況下將遞歸程序轉非遞歸程序,使用自定義棧模擬遞歸過程,幾乎適用於所有遞歸,站在系統的角度,棧能解決所有問題。但是具體問題,也有其他方法轉為非遞歸,如斐波那契數列可使用直接迭代計算出結果。
/**
* 非遞歸實現,不借助棧,直接迭代
* @return
*/
public static int NotRecur(int n){
if(n == 0){
return 0;
} else if(n == 1){
return 1;
} else {
int n0 = 0,
n1 = 1; // n 為0,1時的初值
while(n >= 2){
int tmp = n1 + n0;
n0 = n1;
n1 = tmp;
n--;
}
return n1;
}
}
後續有些算法,如二叉樹的遍歷,會分為遞歸實現和非遞歸實現。
在信息處理時,有一類問題需要逐層或逐行遍歷,比如二叉樹的層次遍歷,圖的廣度優先搜索等。
緩沖區,是為了匹配速度,主要解決主機和外設速度不匹配,解決多用戶引起資源競爭問題。