返回一個整數數組中最大子數組的和(有環),整數數組
1.設計思想
(1)首先創建一個一維數組a[],根據用戶輸入的數組長度及數組內容進行存儲數據。
(2)再定義幾個變量,sum用於求和,max為和最大值,num為數組長度。
(3)開始for循環,sum初始化為0,max初始化為a[0]。循環內容為sum+=a[i];如果sum比max大則將sum值賦給max,如果sum小於0,則定義sum=0。直至循環結束,得到最大子數組的和。
(4)尋找a數組最小值,得到其下標j,將j值賦給t。創建數組b,進行兩次循環,第一次循環i=0,每循環一次j值就增加1,b[i]=a[j],當j>=num時,第一次循環結束。進行第二次循環,令sum=0,j=0。每循環一次j值就增加1,b[i]=a[j],當j>=t時,循環結束,便成環。
(5)開始for循環,sum初始化為0,max為未成環之前得到的最大值。循環內容為sum+=b[i];如果sum比max大則將sum值賦給max,如果sum小於0,則定義sum=0。直至循環結束,得到最大子數組的和。
2。源程序代碼

![]()
1 //返回一個一維整數數組最大子數組和最大值(有環)
2 package ketang;
3 import java.util.*;
4 public class SumArray {
5 public static void main(String[] args) {
6 Scanner sca=new Scanner(System.in);
7 System.out.println("輸入整數數組數的個數");
8 int num=sca.nextInt();
9 int a[],b[];
10 a=new int[num];
11 b=new int[num];
12 System.out.println("輸入數組的數");
13 int i;
14 for(i=0;i<num;i++)
15 {
16 a[i]=sca.nextInt();
17 }
18 int t,j=0,sum=0,max=a[0];
19 for(i=0;i<num;i++) //未成環之前找最大值
20 {
21 sum+=a[i];
22 if(max<sum)
23 {
24 max=sum;
25 }
26 if(sum<0)
27 {
28 sum=0;
29 }
30 }
31 /* 實現首尾相接 */
32 int min=a[0];
33 for(i=0;i<num;i++) //找到最小值
34 {
35 if(min>a[i])
36 {
37 min=a[i];
38 j=i;
39 }
40 }
41 t=j; //將最小值下標j值賦給t
42 i=0;
43 while(j<num)
44 {
45 b[i]=a[j];
46 i++;
47 j++;
48 }
49 j=0;
50 while(j<t)
51 {
52 b[i]=a[j];
53 i++;
54 j++;
55 }
56 sum=0; //接著初始化sum為0
57 for(i=0;i<num;i++) //連成環之後找最大值
58 {
59 sum+=b[i];
60 if(max<sum)
61 {
62 max=sum;
63 }
64 if(sum<0)
65 {
66 sum=0;
67 }
68 }
69 System.out.println("最大子數組和為 "+max);
70 }
71 }
The Main Code
3.結果截圖





4.編程總結
此次編程只需在原來程序基礎上進行改進即可,難點在於如何找到連成環的關鍵位置,關鍵位置找到後形成一個新數組,再利用上次的思想進行尋找最大值即可。
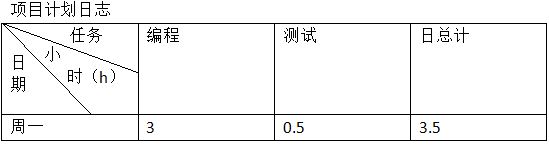
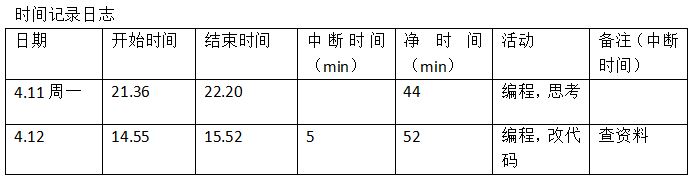
5.psp