閱讀博客的朋友可以到我的網易雲課堂中,通過視頻的方式查看代碼的調試和執行過程:
上一節,我們通過代碼,實現了一個有限狀態自動機,並將其應用於對整形和浮點數的識別。構造有限狀態自動機,並驅動它,從而實現對輸入字符串的識別,整個過程就是詞法分析的本質。
上一節所開發的狀態機,基於以下模型:
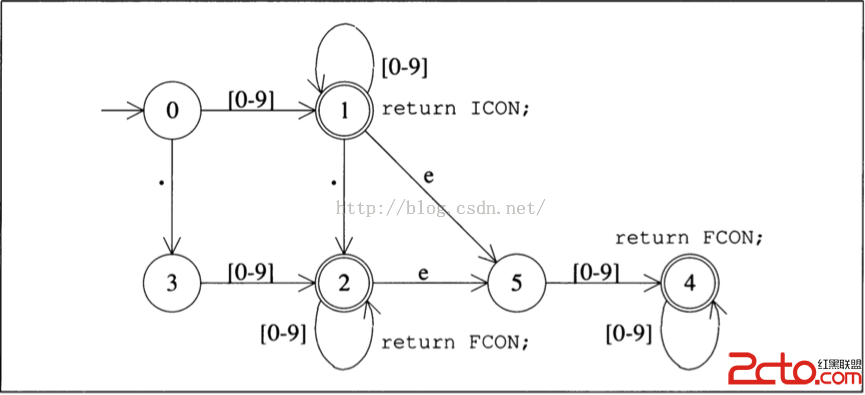
這個模型,是我們在代碼中,手動寫入程序的。實則上,它對應著一組正則表達式:
D[0-9] 表示0-9的字符類
{D}+表示由 0-9 構成的整形數值
({D}+ | {D}*\. {D}+ | {D}+ \. {D}*)(e{D}+)?表示浮點數或科學計數法
其中{D}+ 對應著狀態機中,由0到1,然後在1中自轉這一流程。最後一個正則表達式,對應圖中由狀態0到狀態2,或4的流程。
那麼,問題來了,給定一個正則表達式,可否直接生成一個有限狀態自動機呢?答案是肯定的,大多數正則表達式識別程序,基本上都是先將其轉換為自動機,然後通過驅動自動機來識別輸入的,將正則表達式轉換為有限狀態自動機將是我們這幾節的重點。
有限狀態自動機的分類
有限狀態自動機,其實可以分成兩類。第一類是我們上面給出的,叫做確定性有限狀態自動機: Deterministic finite automaton 簡稱DFA. 確定性的狀態機有一個特點,就是給定當前狀態和輸入字符,那麼下一個狀態就能被唯一確定。例如基於上圖,在狀態1時,接收到字符0-9,那下一個狀態一定只能是1,如果接收到字符 . ,那下一個狀態,就一定只能是2. 更嚴謹的說, DFA 是這樣一種自動機,從給定狀態出去的邊都對應著一個確定的字符,同時,從一個狀態出去的兩條邊,他們對應的字符必定是不同的。
對應於DFA, 另一種狀態機叫非確定性有限狀態機: Nondeterministic finite automaton, 即NFA. 在實踐中,要想順利的將正則表達式轉換為自動機,需要NFA的幫助。NFA 的特點是,從一個狀態出去的兩條邊,可以有相同的對應字符。或者它的邊可以對應一種特殊的字符叫”空”字符,該字符對應的符號是: ?.這種邊表示,不需要任何輸入,就可以從當前狀態進入下一個狀態。
舉個例子,表達式(and | any) , 它對應的DFA如下:
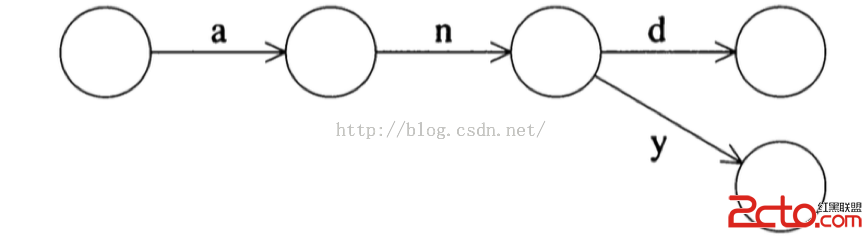
它對應的NFA 如下:
從初始狀態開始,分化出兩條邊,兩條邊對應的字符是一樣的
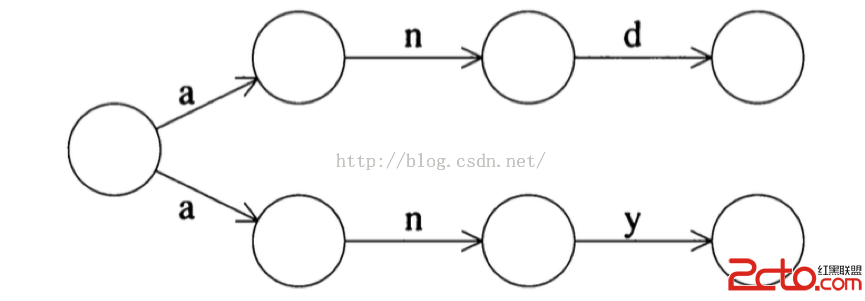
或者:
從初始狀態分化兩條對應字符為空字符的邊,然後分別進入兩個對應的狀態機
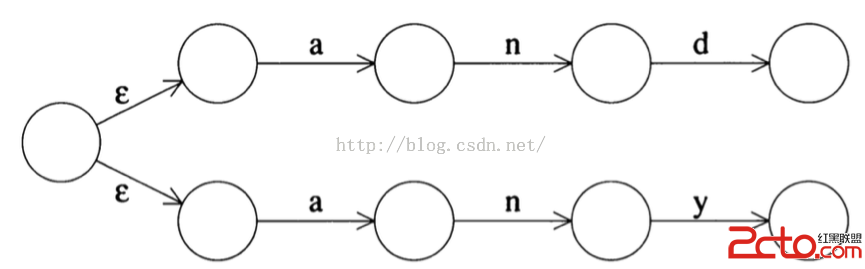
第二種NFA在程序設計中容易實現,因此,在下一節的代碼中,我們將采用第二種NFA的實現模式。
NFA有一個明顯的弱點就是,在代碼設計中,很難用數據結構來對它進行表示。特別是,當對應於一個輸入字符,NFA可以跳轉到多個狀態,那麼,要想利用NFA去識別輸入字符串就比較困難。一般而言,使用NFA的程序都需要經過下兩個步驟:將正則表達式轉換為NFA, 將NFA轉換為DFA. 在後面的討論中,我們將通過代碼來展示這兩種轉換.
Thompson 構造法
將正則表達式轉換為NFA的算法是由貝爾實驗室的Ken Thompson 給出的,這哥們跟丹尼斯.裡奇共同開發了Unix, 而他開發了C語言的前身 B 語言。
他的算法如下:
最簡單的正則表達式是單字符匹配,例如a 匹配輸入字符”a”, 那麼該表達式的NFA 構造如下:
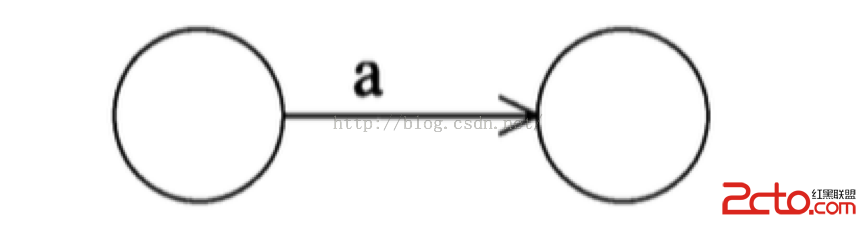
那麼,兩個這樣的正則表達式合成的連接表達式ab 可以表示如下:

實際上,它是先分別構造出兩個表達式的NFA, 然後通過一條?邊,將兩個NFA首尾連接起來。
下面我們看看,兩個表達式進行 OR 操作的時候 | ,NFA怎麼構造,構造圖如下:
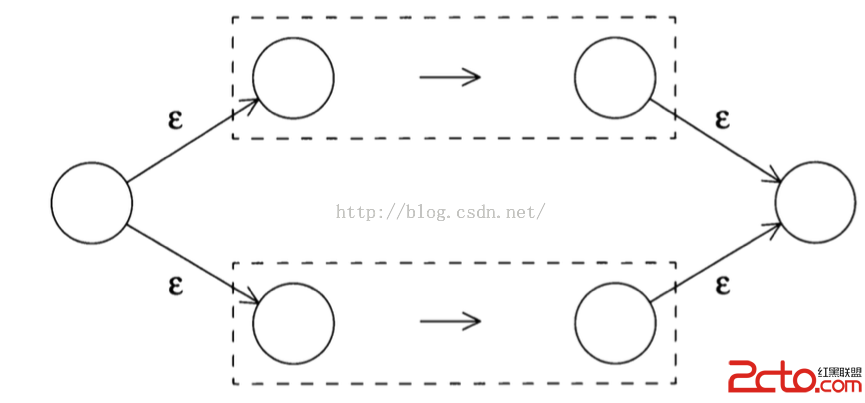
要構造兩個表達式的或操作: exp1 | exp2, 根據圖示,首先分別構造兩個表達式exp1 , exp2 各自的NFA: NFA1(上頭虛線框), NFA2(下頭虛線框), 然後再構造兩個狀態,初始狀態(開頭圓圈節點),和結束狀態(末尾圓圈節點),初始狀態延生處兩條 ? 邊,分別指向NFA1 和 NFA2 的開頭,然後NFA1 和 NFA2的結尾各自延生出一條?邊,分別共同指向結束狀態。
我們再看看 a | b 的NFA圖:
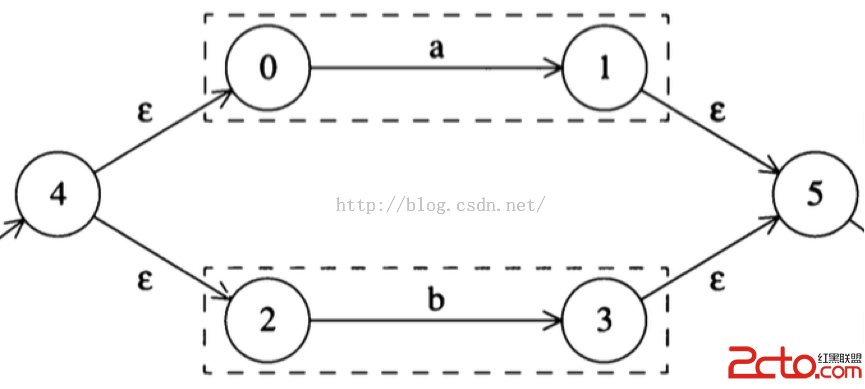
其原理跟前面所描述的是一樣的。上頭虛線框是表達式 a 的NFA, 下頭虛線框是表達式 b 的NFA. 兩個NFA的連接跟前面描述的一模一樣
如果表達式是( (a|b) | cd) 呢,算法也同理,先構造 a | b 的NFA圖,然後構造cd的NFA圖。最後根據前面所說的辦法,再將兩個NFA連接起來:
上頭大虛線框是 (a|d) 的NFA, 下頭長匾虛線框是 cd的NFA. 然後首尾通過兩個狀態節點和ε邊連接起來。

大家可以看到, Thompson構造算法其實是一個自我遞歸的過程
我們再看看相應的閉包操作的構造過程:
exp*的NFA:
如果是自我從復0次,那直接從下面的邊走到末尾節點。
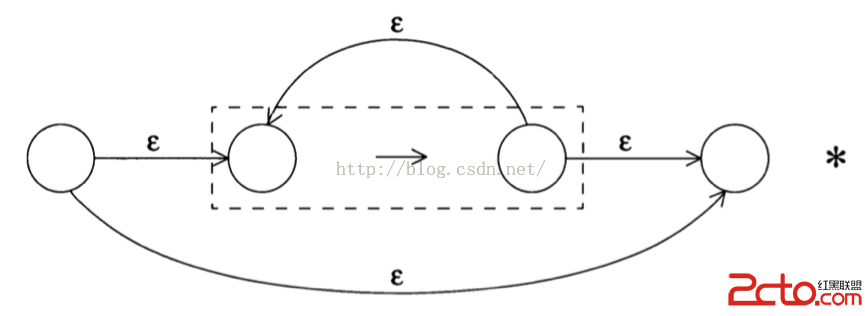
exp+(至少重復一次) 的NFA:
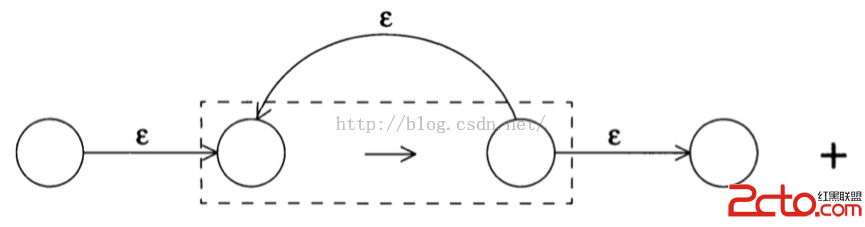
exp?(重復0或1次)的NFA:
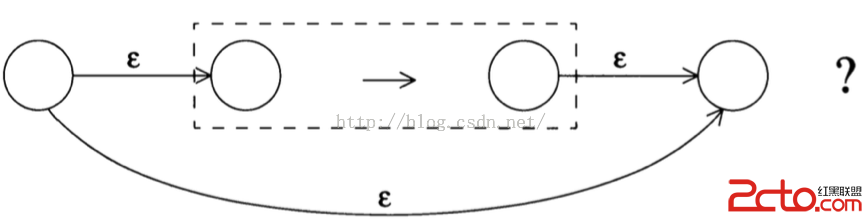
任何復雜的正則表達式它的NFA的構造都是上面幾種構造的組合, 例如表達式
(D*\.D| D\.D*)
構造算法如下:
1.構造 D 的NFA:

2.構造 D*:
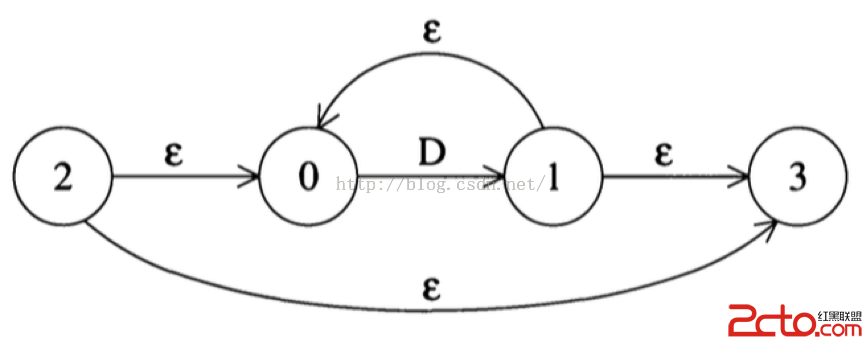
3.構造 D*\.D (由於.在正則表達式中是特殊字符,如果要僅僅想要表達它的符號內容,要在前面加上反斜槓做轉義):
. 號的前部分是D*, 後部分是 D 的NFA.
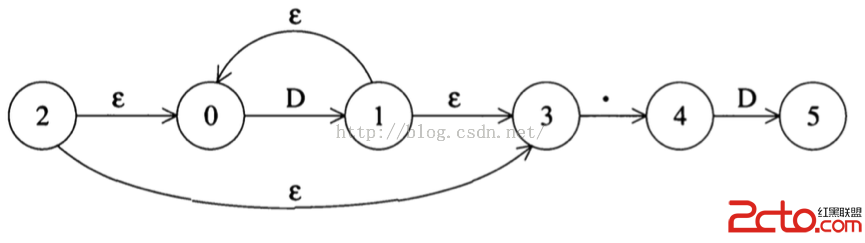
4.構造 D\.D*, 該表達式的NFA其實就是將上圖 . 後面的部分挪到開頭。
5.根據OR 的構造法, 構造整個表達式 (D*\.D | D\.D*)的NFA:
上頭是 D*\.D 的NFA, 下頭是 D\.D*的NFA
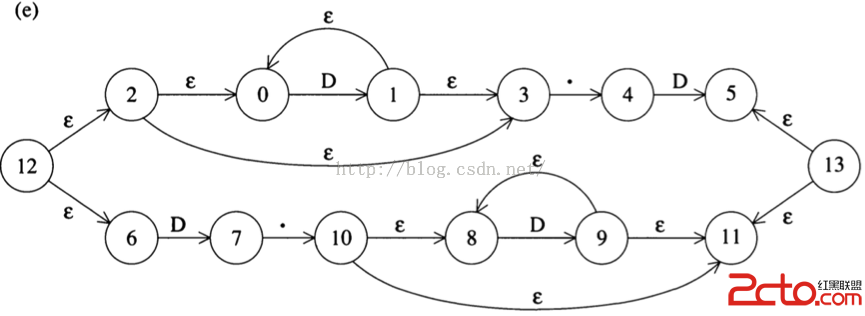
再復雜的表達式的NFA的構造,都是幾種基礎構造的重復組合運用。
我們這一節對概念和算法的介紹就到這裡,根據我的習性,下一節肯定就是上代碼了。