算法基礎——經典八大排序算法的Java及Python實現
概述
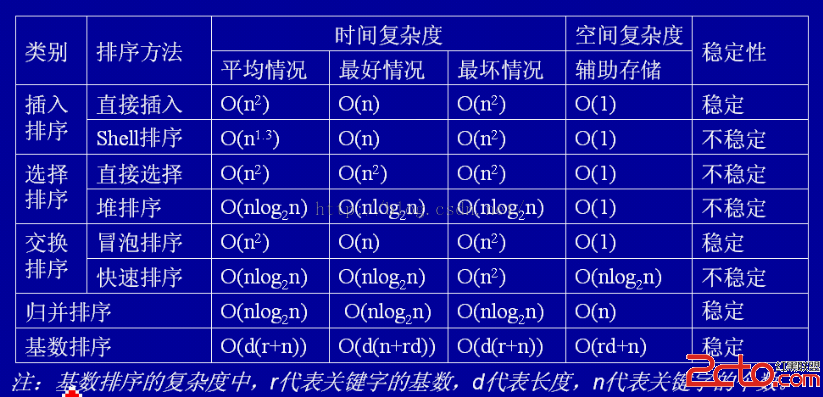
八大排序算法不用多說了,程序員算法基礎必須要掌握的,現在總結一下加深記憶。下圖是這八大排序算法的分類、名稱、時間空間復雜度,以及穩定性。
代碼
以下是經典八大排序算法的Java及Python代碼,都是基於經典算法書籍《算法導論》裡的偽代碼實現的,我在關鍵語句部分附上了注釋。
按照上圖中的順序分別介紹八大排序算法的實現(升序),前面是Java,後面是Python。Java的排序函數寫在了一個類裡,Python的排序函數則直接寫出來了。
直接插入排序
public class InsertSort {
//插入排序,最好情況O(n),最壞情況O(n^2),穩定原址排序
public int[] Sort(int[] arr){
for(int i=0;i=0 && arr[j]>key;j--)
arr[j+1] = arr[j];//注意!這裡不是交換,而是把比key大的都往後挪
arr[j+1] = key;//key再插入合適的位置
}
return arr;
}
}
def insertSort(arr):
#插入排序,最壞為O(n^2),最好為O(n)
#升序排列一個數組,降序排列將while語句中改為arr[i]=0 and arr[i]>key):
#從後往前比較待插入的數和當前數,將arr[j-1]、arr[j-2]...向右移動直到找到arr[j]的適當位置
arr[i+1] = arr[i]
i -= 1
arr[i+1] = key#遍歷完將arr[j]插入到該位置
return arr
希爾排序
public class ShellSort {
// 希爾排序,最好情況O(n),最壞情況O(n^2),平均情況比直接插入排序要好,平均情況為O(n^1.3)
//不穩定,原址排序
public int[] Sort(int[] arr) {
int n = arr.length;
for (int gap = n; gap > 0; gap/=2) {
for (int i = gap;i < n;i++){
if (arr[i] < arr[i-gap]){//如果比前面的元素小,則以步長為gap進行插入排序
int key = arr[i];
int j = i-gap;
while (j>=0 && arr[j] > key){
arr[j+gap] = arr[j];
j -= gap;
}
arr[j+gap] = key;
}
}
}
return arr;
}
}
def shellSort(arr):
#改進版的插入排序-希爾排序,最壞為O(n^2),最好為O(n),平均為O(n^1.3)
gap = len(arr)/2
while gap > 0:
for i in range(gap,len(arr)):
if arr[i] < arr[i-gap]:#後面的元素比前面的小,以gap為步長進行插入排序
key = arr[i]
j = i - gap
while j>=0 and arr[j]>key:
arr[j+gap] = arr[j]
j -= gap
arr[j+gap] = key
#步長減一半
gap /= 2
return arr
直接選擇排序
public class SelectSort {
//選擇排序,最壞和最好都為O(n^2),不穩定,原址排序
public int[] Sort(int[] arr) {
int n = arr.length;
if (n<2)
return arr;
for(int i=0;idef selectSort(arr):
#選擇排序,最壞為O(n^2)
#升序排列一個數組,降序排列將while語句中改為arr[i]堆排序
public class HeapSort {
//維護一個最大堆,使其以i節點的元素為根
public void maxHeapify(int[] arr,int i,int heap_size){
int l = 2*i+1;//左孩子節點
int r = l+1;
int largest = i;
if(larr[largest])
largest = l;
if(rarr[largest])
largest = r;
if(largest != i){
//保證i節點為最大,並維護以largest節點為根的最大堆
int tmp = arr[i];
arr[i] = arr[largest];
arr[largest] = tmp;
maxHeapify(arr,largest,heap_size);
}
}
public void buildMaxHeap(int[] arr){
int heap_size = arr.length;
int mid = (heap_size-1)/2;
//從中間節點開始把arr建為最大堆(只需遍歷數組的一半),最後使得arr[0]為最大堆的根
for(int i=mid;i>=0;i--)
maxHeapify(arr,i,heap_size);
}
public int[] Sort(int[] arr){
//先把數組建造為最大堆
buildMaxHeap(arr);
//從後往前遍歷,根據最大堆的性質arr[0]最大
for(int i = arr.length-1;i>=0;i--){
int tmp = arr[0];
arr[0] = arr[i];
arr[i] = tmp;
int heap_size = i;
maxHeapify(arr,0,heap_size);
}
return arr;
}
}
def maxHeapify(arr,i,heap_size):
#維護一個最大堆,讓arr[i]的值在最大堆中逐級下降,使得以i為根節點的子樹是最大堆,O(lgn)
l = 2*i+1#下標i從0開始,因此左孩子節點的下標是2*i+1
r = l + 1#右孩子節點
largest = i
if larr[largest]:#注意heap_size初始化為len(arr),這裡判斷應為larr[largest]:
largest = r
if largest != i:#i不是最大堆的根節點,就交換值,並且讓largest為根節點的子樹保持最大堆
arr[largest],arr[i] = arr[i],arr[largest]
maxHeapify(arr,largest,heap_size)
def buildMaxHeap(arr):
#自頂向上,將arr轉換為最大堆
heap_size = len(arr)
mid = int((heap_size-1)/2)
for i in range(mid,-1,-1):
maxHeapify(arr,i,heap_size)
def heapSort(arr):
buildMaxHeap(arr)#時間復雜度O(n)
size = len(arr)
#n-1次調用maxHeapify,時間復雜度O(nlgn)
for i in range(size-1,-1,-1):
arr[i],arr[0] = arr[0],arr[i]#從後往前存儲,根據最大堆性質,arr[0]是當前最大堆的最大值
heap_size = i
maxHeapify(arr,0,heap_size)
冒泡排序
public class PopSort {
public int[] Sort(int[] arr) {
int n = arr.length;
if(n<2)
return arr;
for(int i=0;ii;j--){
if(arr[j-1]>arr[j]){
int tmp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = tmp;
}
}
return arr;
}
}
def popSort(arr):
n = len(arr)
if n < 2:
return arr
for i in range(n):
for j in range(n-1,i,-1):
if arr[j-1] > arr[j]:
arr[j-1],arr[j] = arr[j],arr[j-1]
return arr
快速排序
public class QuickSort {
public int getPartition(int[] arr,int low,int high){
int tmp;
int index = low - 1;
for(int i = low;idef quickSort(arr,low,high):
#隨機選擇基准元素的快速排序,達到期望時間復雜度O(nlgn)
#注意high是最大下標
if low < high:
mid = getPartition(arr,low,high)
#對基准元素兩邊的數組快排
quickSort(arr,low,mid-1)
quickSort(arr,mid+1,high)
def getPartition(arr,low,high):
#隨機選擇一個數並與arr[high]交換,防止最壞情況
#將arr[high]作為基准進行排序
rand = random.randint(low,high)
arr[high],arr[rand] = arr[rand],arr[high]
index = low - 1
for i in range(low,high):
if arr[i] <= arr[high]:#保證index前面的數都比key小
index += 1
arr[index],arr[i] = arr[i],arr[index]
arr[index+1],arr[high] = arr[high],arr[index+1]
return index+1
歸並排序
public class MergeSort {
public void Sort(int[] arr,int low,int high){
if(lowdef mergeSort(arr,p,r):
#p17,歸並排序,O(nlgn).注意r是數組的最大下標
if p基數排序
這個用Java寫太麻煩了,各種麻煩的ArrayList操作~~所以只貼Python版
def cntDigit(arr,radix):
#獲取數組元素的最大位數
maxnum = arr[0]
for x in arr:
if x > maxnum:
maxnum = x
cnt = 0
while(maxnum != 0):
maxnum /= radix
cnt += 1
return cnt
def radixSort(arr,radix=10):
k = cntDigit(arr,radix)#獲取最大位數
bucket = [[] for i in range(radix)]
for i in range(1,k+1):
for j in arr:
#bucket[x]存儲從低到高第i位為x的數,如數組中的543,i=1時存在bucket[3]裡
bucket[j/(radix**(i-1)) % (radix)].append(j)
del arr[:]#先初始化arr
#print(bucket)
for z in bucket:#當前位數的數組按順序放入arr中
arr += z
del z[:]
return arr
