一、java數據類型圖如下

二、java基本數據類型講解以及取值范圍
(一)整數類型
1、byte類型
byte在計算機中是占8位的,而且byte是有符號整形,用二進制表示時候最高位為符號位0代表正數1代表負數。默認是0。
取值范圍:-128到127(-2的7次方到2的7次方減1)
擴展(取值范圍計算):
正數在計算機中是以原碼形式存在的,負數在計算機中是以其補碼形式存在的,就是負數的絕對值的原碼轉為二
進制再按位取反後加1。
我們來看-128絕對值128的二進制表示:1000 0000按位取反0111 1111加1後:1000 0000,也就是說-128在計算機
中的表示就是1000 0000了,再來看一下-129在計算機中的表示絕對值129的范圍已經超出了了byte的位
數。所以要注意這類問題。
2、short類型
short(短整型)一個short 16位,取值范圍為-32768~32767,在內存中占用2個字節(-2的15次方到2的15次方-1)默認是0
3、int類型
int(整型)一個int 32位,取值范圍為(-2147483648~2147483647),在內存中占用4個字節(-2的31次方到2的31次方-1)默認是0
4、long類型
long(長整型)一個long 64位,取值范圍為(-9223372036854774808~9223372036854774807),在內存中占用8個字節(-2的63
次方到2的63次方-1)默認是0L或0l推薦用大寫。
可以看到byte和short的取值范圍比較小,而long的取值范圍太大,占用的空間多基本上int可以滿足我們的日常的計算了,而且
int也是使用的最多的整型類型了。在通常情況下,如果JAVA中出現了一個整數數字比如35,那麼這個數字就是int型的,但是如果要表
示long型的就一定要在數據後面加"L"。
byte深入測試(其他類型同理):
public static void main(String[] args) {
/**
* byte類型賦值問題: 負數需要在數值類型前加“-”,如果不標明則說明是正數(-表示負數,+表示正數,+可省略)
* 數值(正數或負數)首位沒有0,則默認為十進制 數值(正數或負數)首位包含0(除0x為首位的情況),則表明為八進制(如:011)
* 數值(正數或負數)首位包含0x,則表明為十六進制(如:0x11或0X11)
* 將八進制、十進制、十六進制強制類型轉換成byte類型,會丟失精度,byte取值范圍為:-128到127
*/
// 八進制(十進制為9),該值輸出為9
byte byte_bajinzhi = 011;
// 八進制(十進制為-9),該值輸出為-9
byte byte_bajinzhi_fushu = -011;
// 八進制(十進制為585,超出byte取值范圍),該值輸出結果為,十進制為73(0111八進制)
byte byte_bajinzhi_zhuanhuan = (byte) 01111;
// 十進制,該值輸出結果不變為111
byte byte_shijinzhi = 111;
// 十進制,超過byte取值范圍,此值輸出結果為-127
// 注意:正數在計算機的存儲就是此正數的原碼;負數在計算機的存儲為負數的絕對值的原碼轉為二進制再按位取反後加1
// 計算過程:129在計算機存儲的,原碼為:127+2(10000001)(說明:127為01111111,加2後10000001,
// 10000001為計算機的存儲,可以看出此值為負數,將首位1去掉,轉換來打印到控制台,轉換方式:先減1,為0000000,然後按位取反得1111111(127),則最後輸出結果為-127)
byte byte_shijinzhi_zhuanhuan = (byte) 129;
// 十六進制(十進制為17),該值輸出為17
byte byte_shiliujinzhi = 0x11;
// 八進制(十進制為-17),該值輸出為-17
byte byte_shiliujinzhi_fushu = -0x11;
System.out.println("byte_bajinzhi:" + byte_bajinzhi);
System.out.println("byte_bajinzhi:" + byte_bajinzhi_fushu);
System.out
.println("byte_bajinzhi_zhuanhuan:" + byte_bajinzhi_zhuanhuan);
System.out.println("byte_shijinzhi:" + byte_shijinzhi);
System.out.println("byte_shijinzhi_zhuanhuan:"
+ byte_shijinzhi_zhuanhuan);
System.out.println("byte_shiliujinzhi:" + byte_shiliujinzhi);
System.out
.println("byte_shiliujinzhi_fushu:" + byte_shiliujinzhi_fushu);
}
測試結果如下:
byte_bajinzhi:9
byte_bajinzhi:-9
byte_bajinzhi_zhuanhuan:73
byte_shijinzhi:111
byte_shijinzhi_zhuanhuan:-127
byte_shiliujinzhi:17
byte_shiliujinzhi_fushu:-17
(二)浮點類型
1、float類型
內存結構如下:
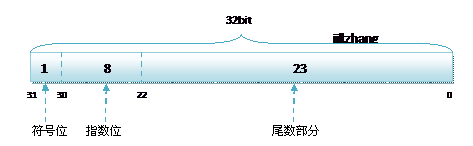
1bit(符號位) 8bits(指數位) 23bits(尾數位)
2、double類型
內存結構如下:
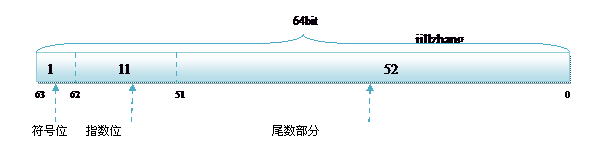
1bit(符號位) 11bits(指數位) 52bits(尾數位)
於是,float的指數范圍為-128~+127,而double的指數范圍為-1024~+1023,並且指數位是按補碼的形式來劃分的。
其中負指數決定了浮點數所能表達的絕對值最小的非零數;而正指數決定了浮點數所能表達的絕對值最大的數,也即決定了浮點數的取值范圍。
float的范圍為-2^128 ~ +2^127,也即-3.40E+38 ~ +3.40E+38;double的范圍為-2^1024 ~ +2^1023,也即-1.79E+308 ~ +1.79E+308。
3、精度討論
float和double的精度是由尾數的位數來決定的。浮點數在內存中是按科學計數法來存儲的,其整數部分始終是一個隱含著的“1”,由於它是不變的,故不能對精度造成影響。
float:2^23 = 8388608,一共七位,由於最左為1的一位省略了,這意味著最多能表示8位數: 2*8388608 = 16777216 。有8位有效數字,但絕對能保證的為7位,也即float的
精度為7~8位有效數字;double:2^52 = 4503599627370496,一共16位,同理,double的精度為16~17位。
對於小數來說,更容易會因為精度而出錯誤。
測試:
測試代碼:
float f = 2.2f;
double d = (double) f;
System.out.println(d);
f = 2.25f;
d = (double) f;
System.out.println(d);
測試結果:
2.200000047683716
2.25
------------------------------------------------------------------------------------測試結果分析-----------------------------------------------------------------------------------------------------------------------------
首先我們看看2.25的單精度存儲方式,轉化為2進制位便是10.01,整理為1.001*2 很簡單
於是我們可以寫出2.25的內存分布:
符號位為:0
指數為1,用補碼表示 0000 0001,轉為移碼就是1000 0001。
尾數位為0010 0000 0000 0000 0000 000
而2.25的雙精度表示為:0 100 0000 0001 0010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,這樣2.25在進行強制轉換的時候,數值是不會變的,而我們再
看看2.2呢,2.2用科學計數法表示應該為:將十進制的小數轉換為二進制的小數的方法為將小數*2,取整數部分,所以0.282=0.4,所以二進制小數第一位為0.4的整數部分0,0.4×2
=0.8,第二位為0,0.8*2=1.6,第三位為1,0.6×2 = 1.2,第四位為1,0.2*2=0.4,第五位為0,這樣永遠也不可能乘到=1.0,得到的二進制是一個無限循環的排列 0011001100110011
0011... ,對於單精度數據來說,尾數只能表示24bit的精度,所以2.2的float存儲為

但是這樣存儲方式,換算成十進制的值,卻不會是2.2的,因為十進制在轉換為二進制的時候可能會不准確,如2.2,而double類型的數據也存在同樣的問題,所以在浮點數表示中會產生些許的誤差,在單精度轉換為雙精度的時候,也會存在誤差的問題,如下面的代碼,輸出結果就不一樣: