以一個M×N的長方陣表示迷宮,0和1分別表示迷宮中的通路和障礙。設計程序,對任意設定的迷宮,求出從入口到出口的所有通路。
下面我們來詳細講一下迷宮問題的回溯算法。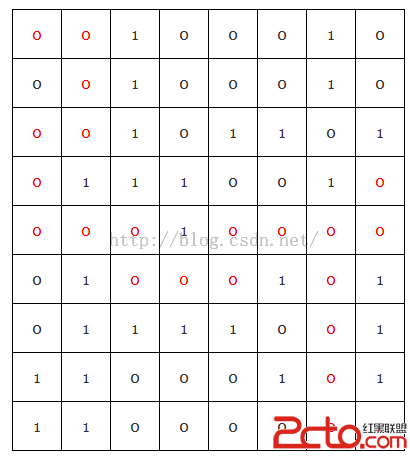
該圖是一個迷宮的圖。1代表是牆不能走,0是可以走的路線。只能往上下左右走,直到從左上角到右下角出口。
做法是用一個二維數組來定義迷宮的初始狀態,然後從左上角開始,不停的去試探所有可行的路線,碰到1就結束本次路徑,然後探索其他的方向,當然我們要標記一下已經走的路線,不能反復的在兩個可行的格子之間來回走。直到走到出口為止,算找到了一個正確路徑。
程序如下,具體做法看注釋即可。
package huisu;
/**
* Created by wolf on 2016/3/21.
*/
public class MiGong {
/**
* 定義迷宮數組
*/
private int[][] array = {
{0, 0, 1, 0, 0, 0, 1, 0},
{0, 0, 1, 0, 0, 0, 1, 0},
{0, 0, 1, 0, 1, 1, 0, 1},
{0, 1, 1, 1, 0, 0, 1, 0},
{0, 0, 0, 1, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 1, 0, 1},
{0, 1, 1, 1, 1, 0, 0, 1},
{1, 1, 0, 0, 0, 1, 0, 1},
{1, 1, 0, 0, 0, 0, 0, 0}
};
private int maxLine = 8;
private int maxRow = 9;
public static void main(String[] args) {
System.out.println(System.currentTimeMillis());
new MiGong().check(0, 0);
System.out.println(System.currentTimeMillis());
}
private void check(int i, int j) {
//如果到達右下角出口
if (i == maxRow - 1 && j == maxLine - 1) {
print();
return;
}
//向右走
if (canMove(i, j, i, j + 1)) {
array[i][j] = 5;
check(i, j + 1);
array[i][j] = 0;
}
//向左走
if (canMove(i, j, i, j - 1)) {
array[i][j] = 5;
check(i, j - 1);
array[i][j] = 0;
}
//向下走
if (canMove(i, j, i + 1, j)) {
array[i][j] = 5;
check(i + 1, j);
array[i][j] = 0;
}
//向上走
if (canMove(i, j, i - 1, j)) {
array[i][j] = 5;
check(i - 1, j);
array[i][j] = 0;
}
}
private boolean canMove(int i, int j, int targetI, int targetJ) {
// System.out.println("從第" + (i + 1) + "行第" + (j + 1) + "列,走到第" + (targetI + 1) + "行第" + (targetJ + 1) + "列");
if (targetI < 0 || targetJ < 0 || targetI >= maxRow || targetJ >= maxLine) {
// System.out.println("到達最左邊或最右邊,失敗了");
return false;
}
if (array[targetI][targetJ] == 1) {
// System.out.println("目標是牆,失敗了");
return false;
}
//避免在兩個空格間來回走
if (array[targetI][targetJ] == 5) {
// System.out.println("來回走,失敗了");
return false;
}
return true;
}
private void print() {
System.out.println("得到一個解:");
for (int i = 0; i < maxRow; i++) {
for (int j = 0; j < maxLine; j++) {
System.out.print(array[i][j] + " ");
}
System.out.println();
}
}
}
我把打印每一步路徑判斷的地方注釋掉了,放開注釋就能看到所有走的路徑。
原本只看圖時我還以為只有3條路徑,沒想到程序打出來了8條。後來仔細看看,果然是有8條路徑……
打印結果如下,5是用來標記路徑的:
1458551044499 得到一個解: 5 5 1 0 0 0 1 0 5 5 1 0 0 0 1 0 5 0 1 0 1 1 0 1 5 1 1 1 0 0 1 0 5 5 5 1 5 5 5 0 0 1 5 5 5 1 5 1 0 1 1 1 1 0 5 1 1 1 0 0 0 1 5 1 1 1 0 0 0 0 5 0 得到一個解: 5 5 1 0 0 0 1 0 5 5 1 0 0 0 1 0 5 0 1 0 1 1 0 1 5 1 1 1 5 5 1 0 5 5 5 1 5 5 5 0 0 1 5 5 5 1 5 1 0 1 1 1 1 0 5 1 1 1 0 0 0 1 5 1 1 1 0 0 0 0 5 0 得到一個解: 5 5 1 0 0 0 1 0 0 5 1 0 0 0 1 0 5 5 1 0 1 1 0 1 5 1 1 1 0 0 1 0 5 5 5 1 5 5 5 0 0 1 5 5 5 1 5 1 0 1 1 1 1 0 5 1 1 1 0 0 0 1 5 1 1 1 0 0 0 0 5 0 得到一個解: 5 5 1 0 0 0 1 0 0 5 1 0 0 0 1 0 5 5 1 0 1 1 0 1 5 1 1 1 5 5 1 0 5 5 5 1 5 5 5 0 0 1 5 5 5 1 5 1 0 1 1 1 1 0 5 1 1 1 0 0 0 1 5 1 1 1 0 0 0 0 5 0 得到一個解: 5 0 1 0 0 0 1 0 5 5 1 0 0 0 1 0 5 5 1 0 1 1 0 1 5 1 1 1 0 0 1 0 5 5 5 1 5 5 5 0 0 1 5 5 5 1 5 1 0 1 1 1 1 0 5 1 1 1 0 0 0 1 5 1 1 1 0 0 0 0 5 0 得到一個解: 5 0 1 0 0 0 1 0 5 5 1 0 0 0 1 0 5 5 1 0 1 1 0 1 5 1 1 1 5 5 1 0 5 5 5 1 5 5 5 0 0 1 5 5 5 1 5 1 0 1 1 1 1 0 5 1 1 1 0 0 0 1 5 1 1 1 0 0 0 0 5 0 得到一個解: 5 0 1 0 0 0 1 0 5 0 1 0 0 0 1 0 5 0 1 0 1 1 0 1 5 1 1 1 0 0 1 0 5 5 5 1 5 5 5 0 0 1 5 5 5 1 5 1 0 1 1 1 1 0 5 1 1 1 0 0 0 1 5 1 1 1 0 0 0 0 5 0 得到一個解: 5 0 1 0 0 0 1 0 5 0 1 0 0 0 1 0 5 0 1 0 1 1 0 1 5 1 1 1 5 5 1 0 5 5 5 1 5 5 5 0 0 1 5 5 5 1 5 1 0 1 1 1 1 0 5 1 1 1 0 0 0 1 5 1 1 1 0 0 0 0 5 0 1458551044503