給定任意長度的一個集合,用一個數組表示,如{"a", "b","c"},求它的所有子集。結果是{ {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}和一個空集。
下面講的就是如何用一個原始的傻瓜方法(非算法)求它的所有子集。
首先我們知道是它的子集個數是2^length,如果長度是3,那子集就共有2的3次方=8個,包括空集。
求子集,我的做法是對任何一項做判斷,有或者無,用1和0來對應表示。
那麼像這種長度為3的,用二進制來表示就是000、001、010……
其實就是從0-2^3,用2進制表示出來就是所以的子集了。然後把0對應的子項給拿掉,譬如010對應的就是b,011對應的就是bc。只需要從0到2^3-1做一個循環,然後把0-7之間的數用二進制表示出來,再與原集合進行對比。把0對應位置的字符去掉,這樣就得到了所有子集。
原理很簡單,下面是代碼
package huisu;
/**
* Created by wolf on 2016/3/22.
*/
public class GetSet {
private String[] origin = {"a", "b", "c"};
private String[] targetArray;
public static void main(String[] args) {
new GetSet().doJob();
}
private void doJob() {
//獲取將要分解的字符串如果轉為2進制最大是幾
//如字符串是3位,就是2^3。從[0 0 0]到[1 1 1]
int maxLength = (int) Math.pow(2, origin.length);
targetArray = new String[maxLength];
for (int i = 0; i < targetArray.length; i++) {
//十進制轉2進制
targetArray[i] = Integer.toBinaryString(i);
}
buling();
print();
}
/**
* 給空位補0,湊齊位數
*/
private void buling() {
for (int i = 0; i < targetArray.length; i++) {
//位數是完整的,不需要補0
if (targetArray[i].length() == origin.length) {
continue;
}
String temp = "";
//0,1,10,11,111
for (int j = 0; j < origin.length - targetArray[i].length(); j++) {
temp += "0";
}
targetArray[i] = temp + targetArray[i];
}
}
private void print(){
for (int i = 0; i < targetArray.length; i++) {
String s = targetArray[i];//如000,001,010
for (int j = 0; j < s.length(); j++) {
char item = s.charAt(j);
if (item == '1') {
System.out.print(origin[j]);
}
}
System.out.println();
}
}
}
在第23行是將10進制的0-7轉成二進制,轉之後如下圖
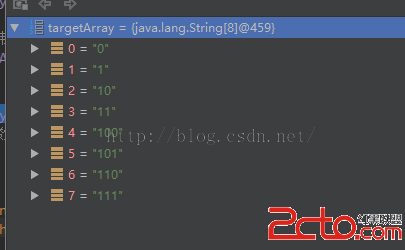
這裡就有個問題,那就是位數並不滿,像0、10之類的,將來和原始數組做對應判斷的時候有點小麻煩,所以我做了個處理,把位數補齊。保持和原始數組位數一樣。
調用了buling(原諒我想不起來用什麼英語來表示補零)方法,把位數不足的前面全補上0.然後就變成了000,001,010……這樣就可以很方便的去判斷了,只打印1所在的位數就行了。參考print方法。
總結:這種做法比較簡單易懂。也能適應任意長度的求子集問題。根據這種做法,還能解決另外一個問題——01背包問題(有編號分別為a,b,c,d,e的五件物品,它們的重量分別是2,2,6,5,4,它們的價值分別是6,3,5,4,6,現在給你個承重為10的背包,如何讓背包裡裝入的物品具有最大的價值總和?)相信很容易能看出來,上面的方法求出來了所有子集,那麼對於01背包問題,就是根據所有的子集,先砍掉所有超重的子集。然後去計算剩余的子集的價值,找到最大的就OK了。