原題重述:(點擊圖片可以進入來源鏈接)
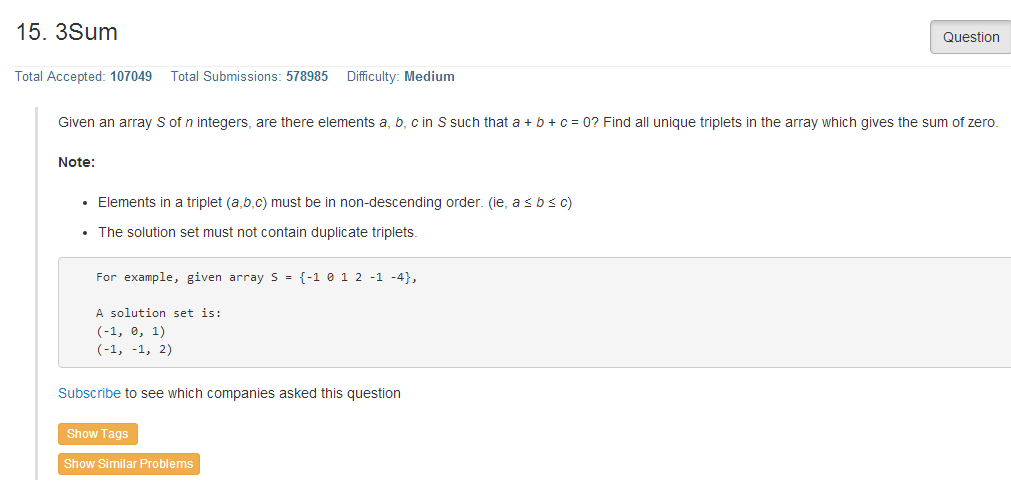
這到題目的中文解釋是,
輸入一個數組,例如{-1 0 1 2 -1 -4},從數組中找三個數(a,b,c),使得其和0,輸出所有的(a,b,c)組合。
要求abc不能重復,並且a<=b<=c。
拿到這個題目的時候,其實每個程序猿都能想到如下的算法,也就是暴力破解,其時間復雜度為o(n^3):
1 for(int i=0;i<nums.length;i++){
2 for(int j=i+1;j<nums.length;j++){
3 for(int k=j+1;k<nums.length;j++){
4 if(nums[i]+nums[j]+nums[k]==0){
5 addResult(nums[i], nums[j], nums[k]);
6 }
7 }
8 }
9 }
首先需要對輸入的數組進行排序,這樣的話由於上面的i<j<k,所以可以保證nums[i]<nums[j]<nums[k]。
其實我的算法的思路就是在暴力破解的基礎上進行優化,盡量降低時間復雜度。
在java中對數組排序的方法是:Arrays.sort(nums);
第三個循環其實是沒有必要的,因為在確定了i,j的值之後,需要尋找的nums[k]的值就已經確定了,即-(nums[i]+nums[j])。
因此無需循環,只需要判斷數組剩下的元素中是否存在這個值就可以了。
基於這個思路我構建了一個hashmap作為hash索引表,用於查找每個值出現的位置:(考慮到一個值可能出現在多個位置的情況,用arraylist)
因為nums是已經排序過的,所以索引表中的arraylist也是已排序好的。
HashMap<Integer, ArrayList<Integer>> index = new HashMap<>();
構建這個索引表的代碼如下:
1 for(int i=0;i<nums.length;i++){
2 int num = nums[i];
3 if(num==0){
4 n++;
5 }
6 if(index.get(num)==null){
7
8
9 index.put(num, new ArrayList<Integer>());
10 }
11
12 index.get(num).add(i);
13
14
15 }
這裡面的n是表示0的個數,如果n>=3,就直接輸出一個[0 0 0]了。
從索引表查詢需要的數的方式,我想了很久,最後想到一個很不錯的方法:
1 int p = -(nums[i]+nums[j]);
2 if(p<0) continue;
3 ArrayList<Integer> in = index.get(p);
4 if(in==null) continue;
5 if(in.get(in.size()-1)>j){
6 if(p>nums[j]){
7 addResult(nums[i], nums[j],p);
8 }else if(p>nums[i]){
9 addResult(nums[i], p,nums[j]);
10 }else{
11 addResult(p,nums[i], nums[j]);
12 }
13
14 }
第2行,為什麼要捨棄p<0的情況?因為要避免重復。如果p也是負數的話,由於nums[i]<nums[j]那麼會出現兩種情況:
①nums[i]和nums[j]都是正數;
②nums[i]是負數,nums[j]是正數 。
那麼在其他的掃描過程中一定會出現:
①那時的nums[i]'=p,p'=nums[i],nums[j]'=nums[j];
②那時的p'=nums[j],nums[i]'=min(nums[i],p),nums[j]'=max(nums[i],p)。
第5行in.get(in.size()-1)>j是什麼意思?
我們這個時候是需要找一個k(k>j),使得nums[k]=p,如果有就輸出nums[k]。
ArrayList in表示使得nums[k]=p的所有k值,如果最大的k值大於j,那不就表示存在k>j,使得nums[k]=p了嗎?
一定要求k>j,因為如下的情況是不符合要求的:
輸入 [-1 0 1 2] 不能輸出 [-1 -1 2] 因為-1的索引是[0],在遍歷時它不滿足k>j
關於避免重復的問題,
我用addResult函數來避免重復,大家一看應該就懂
1 HashSet<String> repeat = new HashSet<String>(); // 查重
2 List<List<Integer>> result = new LinkedList<List<Integer>>();
3
4
5 public void addResult(int n1, int n2, int n3) {
6 String s = n1 + "&"+n2;
7
8 if (!repeat.contains(s)) {
9 List<Integer> p = new ArrayList<>();
10 p.add(n1);
11 p.add(n2);
12 p.add(n3);
13 result.add(p);
14 repeat.add(s);
15 }
16 }
最終詳細的代碼如下:
