K-MEANS算法
摘要:在數據挖掘中,K-Means算法是一種 cluster analysis 的算法,其主要是來計算數據聚集的算法,主要通過不斷地取離種子點最近均值的算法。
在數據挖掘中,K-Means算法是一種cluster analysis的算法,其主要是來計算數據聚集的算法,主要通過不斷地取離種子點最近均值的算法。
K-Means算法主要解決的問題如下圖所示。我們可以看到,在圖的左邊有一些點,我們用肉眼可以看出來有四個點群,但是我們怎麼通過計算機程序找出這幾個點群來呢?於是就出現了我們的K-Means算法(Wikipedia鏈接)
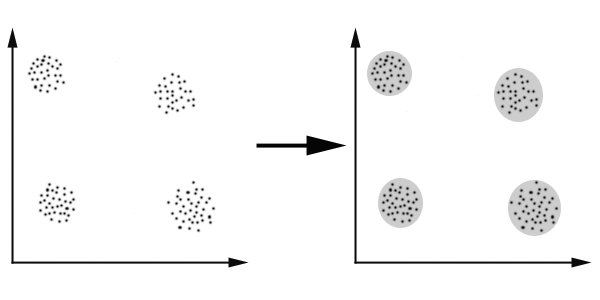
K-Means要解決的問題
算法概要
這個算法其實很簡單,如下圖所示:
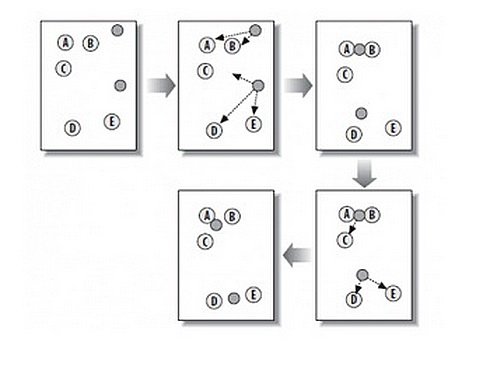
從上圖中,我們可以看到,A,B,C,D,E是五個在圖中點。而灰色的點是我們的種子點,也就是我們用來找點群的點。有兩個種子點,所以K=2。
然後,K-Means的算法如下:
這個算法很簡單,但是有些細節我要提一下,求距離的公式我不說了,大家有初中畢業水平的人都應該知道怎麼算的。我重點想說一下“求點群中心的算法”。
一般來說,求點群中心點的算法你可以很簡的使用各個點的X/Y坐標的平均值。不過,我這裡想告訴大家另三個求中心點的的公式:
1)Minkowski Distance公式——λ可以隨意取值,可以是負數,也可以是正數,或是無窮大。
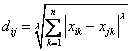
2)Euclidean Distance公式——也就是第一個公式λ=2的情況
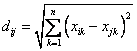
3)CityBlock Distance公式——也就是第一個公式λ=1的情況
![]()
這三個公式的求中心點有一些不一樣的地方,我們看下圖(對於第一個λ在0-1之間)。



(1)Minkowski Distance (2)Euclidean Distance (3) CityBlock Distance
上面這幾個圖的大意是他們是怎麼個逼近中心的,第一個圖以星形的方式,第二個圖以同心圓的方式,第三個圖以菱形的方式。
K-Means的演示
如果你以”K Means Demo“為關鍵字到Google裡查你可以查到很多演示。這裡推薦一個演示:http://home.dei.polimi.it/matteucc/Clustering/tutorial_html/AppletKM.html
操作是,鼠標左鍵是初始化點,右鍵初始化“種子點”,然後勾選“Show History”可以看到一步一步的迭代。
注:這個演示的鏈接也有一個不錯的K Means Tutorial。
K-Means主要有兩個最重大的缺陷——都和初始值有關:
我在這裡重點說一下K-Means++算法步驟:
相關的代碼你可以在這裡找到“implement the K-means++ algorithm”(牆)另,Apache的通用數據學庫也實現了這一算法
看到這裡,你會說,K-Means算法看來很簡單,而且好像就是在玩坐標點,沒什麼真實用處。而且,這個算法缺陷很多,還不如人工呢。是的,前面的例子只是玩二維坐標點,的確沒什麼意思。但是你想一下下面的幾個問題:
1)如果不是二維的,是多維的,如5維的,那麼,就只能用計算機來計算了。
2)二維坐標點的X,Y 坐標,其實是一種向量,是一種數學抽象。現實世界中很多屬性是可以抽象成向量的,比如,我們的年齡,我們的喜好,我們的商品,等等,能抽象成向量的目的就是可以讓計算機知道某兩個屬性間的距離。如:我們認為,18歲的人離24歲的人的距離要比離12歲的距離要近,鞋子這個商品離衣服這個商品的距離要比電腦要近,等等。
只要能把現實世界的物體的屬性抽象成向量,就可以用K-Means算法來歸類了。
在《k均值聚類(K-means)》 這篇文章中舉了一個很不錯的應用例子,作者用亞洲15支足球隊的2005年到1010年的戰績做了一個向量表,然後用K-Means把球隊歸類,得出了下面的結果,呵呵。
其實,這樣的業務例子還有很多,比如,分析一個公司的客戶分類,這樣可以對不同的客戶使用不同的商業策略,或是電子商務中分析商品相似度,歸類商品,從而可以使用一些不同的銷售策略,等等。
總結:
1. 算法流程
輸入:聚類個數k,以及包含 n個數據對象的數據庫。 輸出:滿足方差最小標准的k個聚類。
(1)從n個數據對象任意選擇k個對象作為初始聚類中心
(2)計算每個對象與聚類中心的距離;並根據最小距離重新對相應對象進行劃分
(3)重新計算每個聚類的均值作為新的聚類中心
(4)循環(2)到(3)直到每個聚類不再發生變化為止
2. 算法分析
K-Means的優化目標可以表示為:
其中,x_n表示數據對象,μ_k表示中心點,r_nk在數據點n分配到類別k的時候為1,沒有分配到類別k的時候為0。
整個算法通過迭代計算,找到合適的r_nk和μ_k來,使得J最小。
算法流程的第二步,固定μ_k,更新r_nk,將每個數據對象放到與其最近的聚類中心的類別中,自然這一步能夠保證在固定μ_k的情況下,J的值降到了最小。
算法流程的第三步,固定r_nk,更新μ_k,此時J對μ_k(實際上是μ_0,μ_1,...分別求導)求導並令結果等於零,得到:
即,當新的中心點取每個類別中的中心值的時候,每個類別內部的標准距離下降最多。J是所有類別距離內部的距離之和,因此保證了的固定r_nk的情況下,J的值降到了最小。
兩個步驟,J的值都在下降,隨著迭代次數增加J的值會下降到一個極小值。
3. 結束條件
K-Means迭代的條件可以有如下幾個:
· 每個聚類內部元素不在變化,這是最理想的情況了。
· 前後兩次迭代,J的值相差小於某個阈值。
· 迭代超過一定的次數。
4. 缺點
· K值的設定難以估計,如果數據實際上是10個類別,設K=20,那麼得到的結果很可能不好,如果設K=10,那麼得到的結果很可能會很好。
· K確定了以後,初始中心也是一個問題,K個中心一旦選定了,就決定了聚類結果,選的好,聚類出來的結果就好。
個人認為主要的缺點是這兩個,相應的也有一些改進方法,這裡不涉及了,具體可參見參考中的百度百科_K-Means。
5. 重點
本文主要重點有兩個:
K-Means的三個結束條件(不變化,J值變化較小,迭代次數)和兩個缺點(K值,K個中心點)。
最後給一個挺好的算法的幻燈片:http://www.cs.cmu.edu/~guestrin/Class/10701-S07/Slides/clustering.pdf