除夕全天微信用戶紅包總發送量達到10.1億次,搖一搖互動量達到110億次,紅包峰值發送量為8.1億次/分鐘。
拋開微信紅包的市場價值不談,紅包本身的算法也引發了熱議,由於官方沒有給出明確的說法,各家也是眾說紛纭,小編下面也為大家帶來幾種分析。
首先看看數據分析帝
大多數人都做出自己的猜測,這也是在不知道內部隨機算法的時候的唯一選擇,但是大多數人沒有給出自己親自的調查結果。這裡給出一份100樣本的調查抽樣樣本數據,並提出自己的猜測。
1. 錢包錢數滿足截尾正態隨機數分布。大致為在截尾正態分布中取隨機數,並用其求和數除以總價值,獲得修正因子,再用修正因子乘上所有的隨機數,得到紅包價值。
這種分布意味著:低於平均值的紅包多,但是離平均值不遠;高於平均值的紅包少,但是遠大於平均值的紅包偏多。
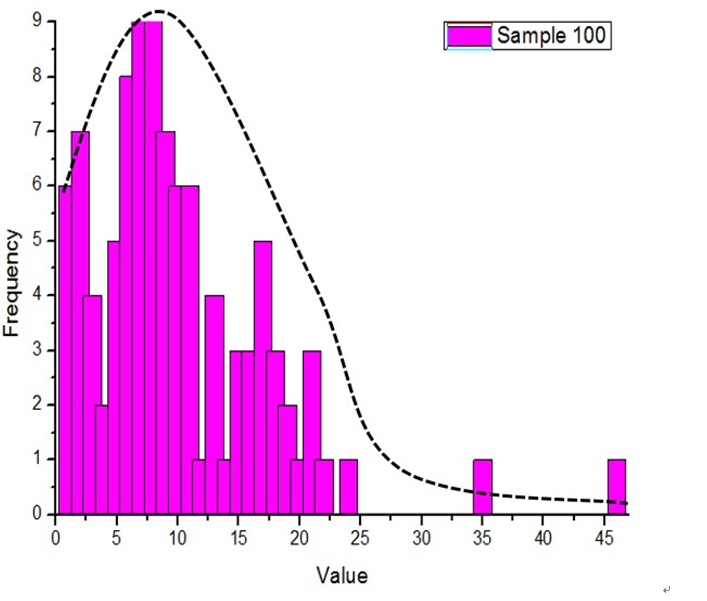
圖1. 錢包價值與其頻率分布直方圖及其正態擬合
但看分布直方圖並不能推出它符合正態分布,但是考慮到程序的簡潔性和隨機數的合理性,這是最合乎情理的一種猜測。
越是後面的錢包,價值普遍更高
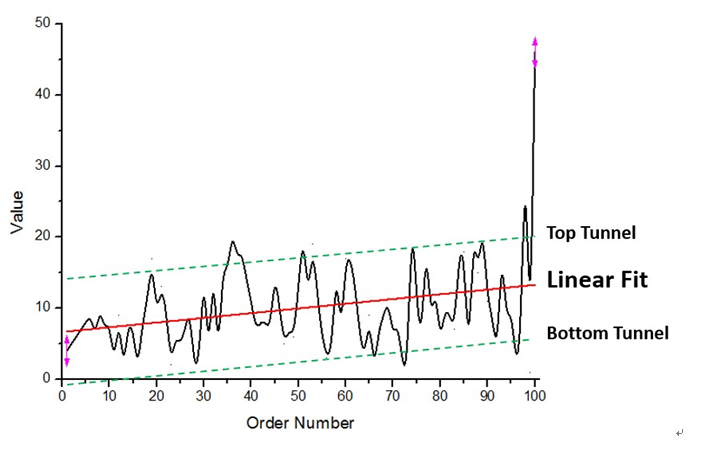
圖2. 錢包序列數與其價值關系曲線
從圖2中的線性擬合紅線可以看到,錢包價值的總體變化趨勢是在慢慢增大,其變化范圍大約是一個綠色虛線上下界劃出的“通道”。(曲線可以被圍在這麼一個正合乎常規的“通道”中,也從側面反映了規律1的合理性,說明了並不是均勻分布的隨機數)
從另一個平均數的圖中也可以看出這一規律。
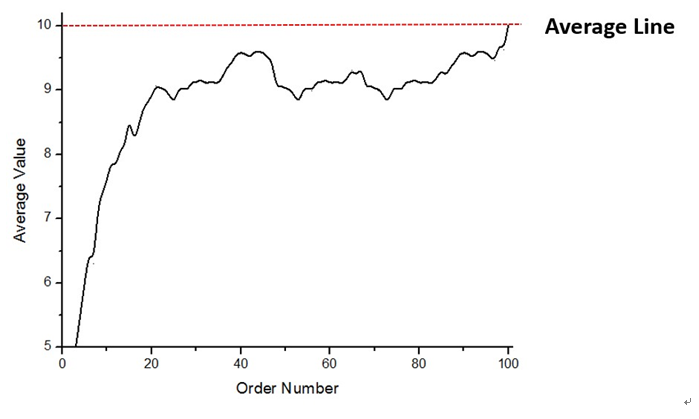
圖3. 平均數隨序列數的變化曲線
在樣本中,1000價值的錢包被分成100份,均值為10。然而在圖3中我們可以看到在最後一個錢包之前,平均數一直低於10,這就說明了一開始的錢包價值偏低,一直被後期的錢包價值拉著往上走,後期的錢包價值更高。
3. 當然平均數的圖還可以透露出另一個規律,那就是最後的那一個人往往容易走運抽得比較多。因為最後那一個人是錢包剩下多少就拿多少的,而之前所有人的平均數 都低於10,所以至少保證了最後一個人會高於平均值。在本樣本中,98號錢包抽到35,而最後一份錢包抽到46。
綜上,根據樣本猜測:
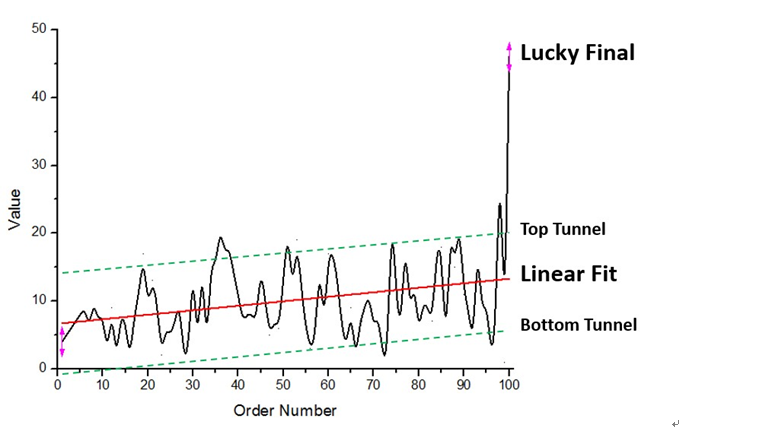
1. 抽到的錢大多數時候跟別人一樣少,但一旦一多,就容易多很多。
2. 越是抽後面的錢包,錢越容易多。
3. 最後一個人往往容易撞大運。
點評:這種明顯很實際有差異,小編每次不管什麼時候搶都是幾毛錢。
第二位同學寫了一個簡單python 代碼
據觀察,紅包分錢滿足以下幾點:
1.不會有人拿不到錢
2.不會提前分完
3.錢的波動范圍很大
紅包在一開始創建的時候,分配方案就訂好了。搶紅包的時候,不過是挨個pop up而已。
因此 python 代碼如下:
def weixin_divide_hongbao(money, n): divide_table = [random.randint(1, 10000) for x in xrange(0, n)] sum_ = sum(divide_table) return [x*money/sum_ for x in divide_table]
不過上述算法還有兩個小問題:
1.浮點數精度問題
2.邊界值的處理
第三位同學按照網上流傳的python寫了一個java的版本
int j=1;
while(j<1000)
{
int number=10;
float total=100;
float money;
double min=0.01;
double max;
int i=1;
List math=new ArrayList();
while(i<number)
{
max = total- min*(number- i);
int k = (int)((number-i)/2);
if (number -i <= 2)
{k = number -i;}
max = max/k;
money=(int)(min*100+Math.random()*(max*100-min*100+1));
money=(float)money/100;
total=total-money;
math.add(money);
System.out.println("第"+i+"個人拿到"+money+"剩下"+total);
i++;
if(i==number)
{
math.add(total);
System.out.println("第"+i+"個人拿到"+total+"剩下0");
}
}
System.out.println("本輪發紅包中第"+(math.indexOf(Collections.max(math))+1)+"個人手氣最佳");
j++;
}
第四位同學的這種算法看起來非常科學。
他認為:
1、每個人都要能夠領取到紅包;
2、每個人領取到的紅包金額總和=總金額;
3、每個人領取到的紅包金額不等,但也不能差的太離譜,不然就沒趣味;
4、算法一定要簡單,不然對不起騰訊這個招牌;
正式編碼之前,先搭建一個遞進的模型來分析規律
設定總金額為10元,有N個人隨機領取:
N=1
則紅包金額=X元;
N=2
為保證第二個紅包可以正常發出,第一個紅包金額=0.01至9.99之間的某個隨機數
第二個紅包=10-第一個紅包金額;
N=3
紅包1=0.01至0.98之間的某個隨機數
紅包2=0.01至(10-紅包1-0.01)的某個隨機數
紅包3=10-紅包1-紅包2
……
int j=1;
while(j<1000)
{
int number=10;
float total=100;
float money;
double min=0.01;
double max;
int i=1;
List math=new ArrayList();
while(i<number)
{
max = total- min*(number- i);
int k = (int)((number-i)/2);
if (number -i <= 2)
{k = number -i;}
max = max/k;
money=(int)(min*100+Math.random()*(max*100-min*100+1));
money=(float)money/100;
total=total-money;
math.add(money);
System.out.println("第"+i+"個人拿到"+money+"剩下"+total);
i++;
if(i==number)
{
math.add(total);
System.out.println("第"+i+"個人拿到"+total+"剩下0");
}
}
System.out.println("本輪發紅包中第"+(math.indexOf(Collections.max(math))+1)+"個人手氣最佳");
j++;
}
輸入一看,波動太大,這數據太無趣了!
第1個紅包:7.48 元,余額:2.52 元
第2個紅包:1.9 元,余額:0.62 元
第3個紅包:0.49 元,余額:0.13 元
第4個紅包:0.04 元,余額:0.09 元
第5個紅包:0.03 元,余額:0.06 元
第6個紅包:0.03 元,余額:0.03 元
第7個紅包:0.01 元,余額:0.02 元
第8個紅包:0.02 元,余額:0 元
改良一下,將平均值作為隨機安全上限來控制波動差
int j=1;
while(j<1000)
{
int number=10;
float total=100;
float money;
double min=0.01;
double max;
int i=1;
List math=new ArrayList();
while(i<number)
{
max = total- min*(number- i);
int k = (int)((number-i)/2);
if (number -i <= 2)
{k = number -i;}
max = max/k;
money=(int)(min*100+Math.random()*(max*100-min*100+1));
money=(float)money/100;
total=total-money;
math.add(money);
System.out.println("第"+i+"個人拿到"+money+"剩下"+total);
i++;
if(i==number)
{
math.add(total);
System.out.println("第"+i+"個人拿到"+total+"剩下0");
}
}
System.out.println("本輪發紅包中第"+(math.indexOf(Collections.max(math))+1)+"個人手氣最佳");
j++;
}
輸出結果見下圖
第1個紅包:0.06 元,余額:9.94 元
第2個紅包:1.55 元,余額:8.39 元
第3個紅包:0.25 元,余額:8.14 元
第4個紅包:0.98 元,余額:7.16 元
第5個紅包:1.88 元,余額:5.28 元
第6個紅包:1.92 元,余額:3.36 元
第7個紅包:2.98 元,余額:0.38 元
第8個紅包:0.38 元,余額:0 元
小結:
小編覺得這完全可以理解成一個紅包引發的血案,小編僅僅列舉了幾個,還有一些工程學的同學直接拋出了數學模型、離散函數等等,但是無論算法是簡單還是復雜,玩的開心就夠了。