迪菲－赫爾曼密鑰交換(Diffie–Hellman)算法原理和PHP實現版

迪菲－赫爾曼(Diffie–Hellman)是一個可以讓雙方在不安全的公共信道上建立秘鑰的一種算法，雙方後期就可以利用這個秘鑰加密(如RC4)內容。
迪菲－赫爾曼(Diffie–Hellman)算法原理很簡單：

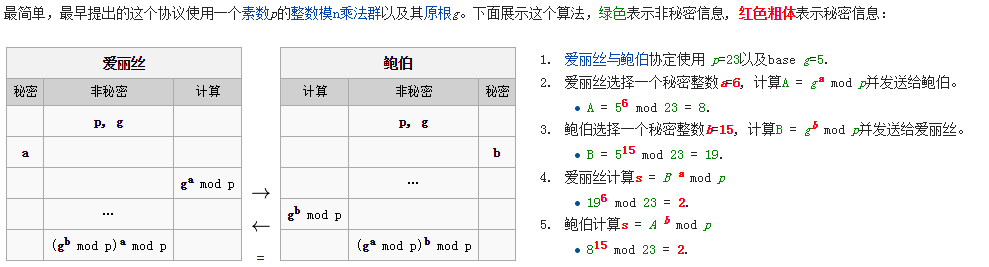
如上原理，最後很容易通過數學原理證明(g^b%p)^a%p = (g^a%p)^b%p，因此它們得到一個相同的密鑰。
上面除了a,b和最後得出的公共密鑰是秘密的，其它都是可以在公共信道上傳遞。實際運用中p很大(300位以上)，g通常取2或5。那麼幾乎不可能從p,g和g^a%p算出a(離散數學問題)。

很多語言都對該算法做了實現，以PHP package中Crypt_DiffieHellman為例：

<?php
include 'DiffieHellman.php';
 
/*
 *   Alice: prime = 563
 *       generator = 5
 *       private key = 9
 *   Bob:  prime = 563
 *       generator = 5
 *       private key = 14
 */
 
$p = 563;
$g = 5;
$alice = new Crypt_DiffieHellman($p, $g, 9);
$alice_pubKey = $alice->generateKeys()->getPublicKey();
 
$bob = new Crypt_DiffieHellman($p, $g, 14);
$bob_pubKey = $bob->generateKeys()->getPublicKey();
 
$alice_computeKey = $alice->computeSecretKey($bob_pubKey)->getSharedSecretKey();
$bob_computeKey = $bob->computeSecretKey($alice_pubKey)->getSharedSecretKey();
 
echo "{$alice_pubKey}-{$bob_pubKey}-{$alice_computeKey}-{$bob_computeKey}"; //78-534-117-117