這幾天看到幾篇關於尾遞歸的文章,之前對尾遞歸沒有多大概念,所以回頭研究了一下尾遞歸。
尾遞歸的概念
尾遞歸(Tail Recursion)的概念是遞歸概念的一個子集。對於普通的遞歸,由於必須要記住遞歸的調用堆棧,由此產生的耗用是難以估量的。比如下文中php小節第一個例子使用php寫一個階乘函數,就是由於遞歸造成了棧溢出的錯誤。尾遞歸出現的目的就是消除遞歸棧耗損這個缺憾的。
從代碼層面看,尾遞歸其實一句話就可以說清楚了:
函數的最後一個操作是遞歸調用
比如"菲波納锲"數列的php的遞歸實現:
復制代碼 代碼如下:
fibonacci.php
<?php
function fibonacci($n) {
if ($n < 2) {
return $n;
}
return fibonacci($n - 1) + fibonacci($n - 2);
}
var_dump(fibonacci(30));
這是遞歸函數,但不是尾遞歸,因為fibonacci的最後一個操作是加法操作。
轉化為尾遞歸:
復制代碼 代碼如下:
function fibonacci2($n, $acc1, $acc2) {
if ($n == 0) {
return $acc1;
}
return fibonacci2($n-1, $acc2, $acc1 + $acc2);
}
fibonacci2就是一個尾遞歸,它增加兩個累加器acc1和acc2,並給出初始的值。記住:遞歸轉化為尾遞歸的思想一定是增加累加器,減少遞歸外操作。
尾遞歸在不同語言上的應用也是不同的。最常使用的就是函數式編程Erlang,幾乎是所有出現遞歸的函數全部都修改成為尾遞歸。下面說一下尾遞歸在幾個不同的語言上的表現和應用。
php中的尾遞歸
我們做個實驗
普通遞歸:
復制代碼 代碼如下:
<?php
function factorial($n)
{
if($n == 0) {
return 1;
}
return factorial($n-1) * $n;
}
var_dump(factorial(100000000));
尾遞歸:
復制代碼 代碼如下:
<?php
function factorial($n, $acc)
{
if($n == 0) {
return $acc;
}
return factorial($n-1, $acc * $n);
}
var_dump(factorial(100000000, 1));
實驗結果:

事實證明,
尾遞歸在php中是沒有任何優化效果的!
C中的尾遞歸
在C中的尾遞歸優化是gcc編譯器做的。在gcc編譯的時候加上-O2會對尾遞歸進行優化
我們可以直接看生成的匯編代碼:
(使用gdb, gcc –O2 factorial.c –o factorial; disass factorial)
未加-O2生成的匯編: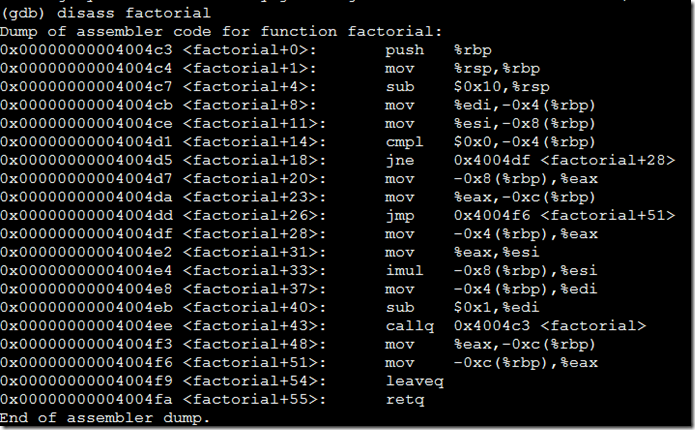
加了O2優化的匯編: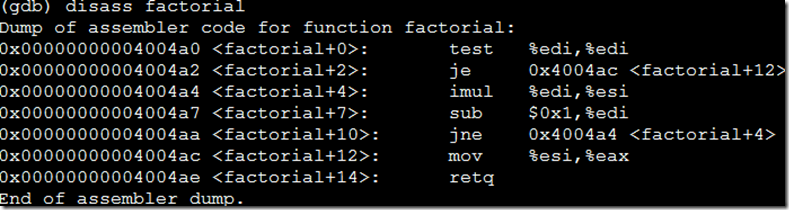
不要頭大,我也是初看匯編,但是這份代碼非常簡單,去網上稍微搜搜命令,大致就能理解:
復制代碼 代碼如下:
function factoral(n, sum) {
while(n != 0){
sum = n * sum
n = n-1
}
return sum
}
gcc做的確實是智能優化。
如果你還有興趣,你可以使用-O3對尾遞歸進行優化,並查看其中的匯編指令
-O3的優化是直接將循環展開
總結
一般的線性遞歸修改成為尾遞歸最大的優勢在於減少了遞歸調用棧的開銷。從php那個例子就明顯看出來遞歸開銷對程序的影響。但是並不是所有語言都支持尾遞歸的,即使支持尾遞歸的語言也一般是在編譯階段對尾遞歸進行優化,比如上例中的C語言對尾遞歸的優化。在使用尾遞歸對代碼進行優化的時候,必須先了解這門語言對尾遞歸的支持。