決策樹之ID3

決策樹之ID3

信息增益的計算：

信息熵：

信息熵，簡稱“熵”。假定訓練集中目標屬性為C，C有C1，C2，…，Cm個取值，每個取值占的比例為P1，P2， …，Pm。則信息熵的定義為：

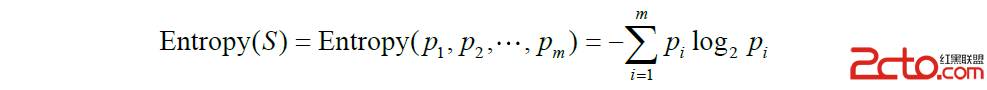
例3-2：現有weather數據集如下，求數據集關於目標屬性 play ball 的信息熵？

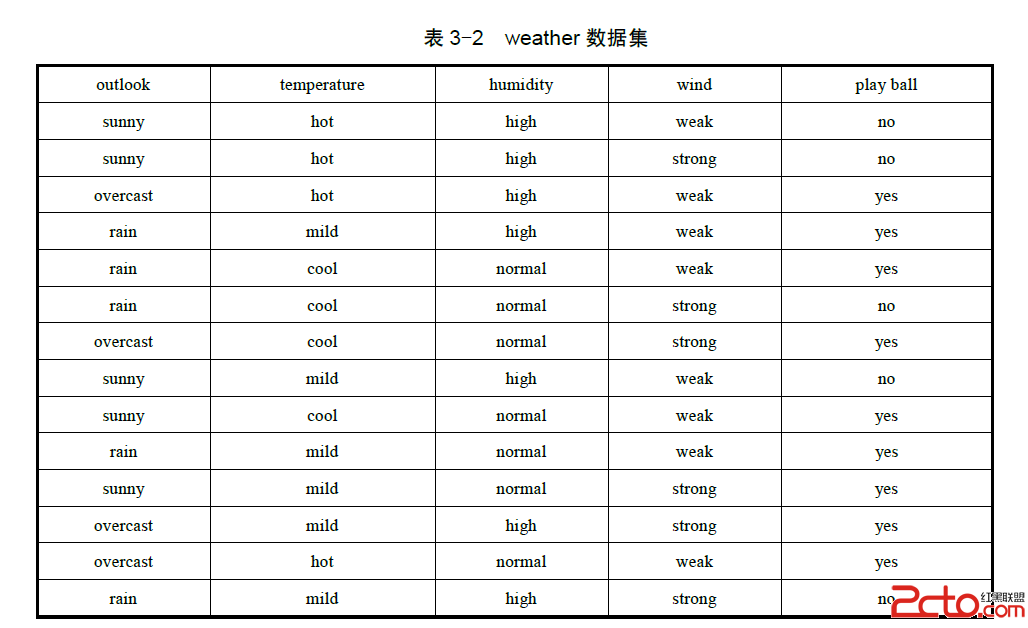
解：把weather數據集記為S，目標屬性 play ball 有“yes”和“no”兩個取值。其中“yes”占的比例為9/14，“no”占的比例為5/14。所以數據集關於目標屬性的信息熵為：

 

 

 

信息增益：

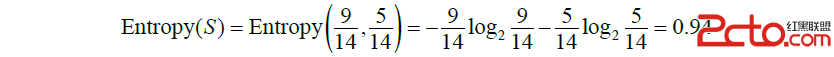
信息增益記為 Gain(S,A) ，公式為：

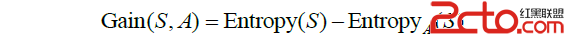
其中 EntrZ喎?http://www.Bkjia.com/kf/ware/vc/" target="_blank" class="keylink">vcHlBKFMpILHtyr6wtMr00NRBu6631lO687XE0fmxvtfTvK+1xOzYoaM8YnIgLz4NCrzZtqjK9NDUIEEg09AgayC49rK7zay1xMih1rWjrLTTtvi9qyBTILuut9bOqiBrILj20fmxvtfTvK8ge1MxLFMyLCZoZWxsaXA7LFNrfaOs1PLT0KO6PGJyIC8+DQo8aW1nIGFsdD0="這裡寫圖片描述" src="http://www.bkjia.com/uploads/allimg/150604/041232FK-4.png" title="\" />
其中，"Si|（i,=1,2,?k）為樣本子集 Si 中包含的樣本數，|S| 為樣本集 S 中包含的樣本數。

例3-3：依據上表weather數據集中的數據，設該數據集為S，假定用wind來劃分S，求S對屬性wind的信息增益。
解：屬性wind有“weak”和“strong”兩個取值，將數據集S劃分為兩部分，記為S1和S2。
其中S1有8個樣本，S2有6個樣本。對樣本集S1、S2的熵：

屬性 wind 劃分 S 後的熵為：

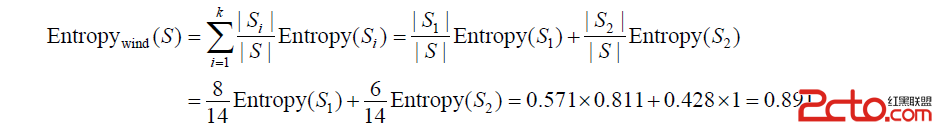
所以，屬性 wind 劃分數據集 S 所得的信息增益為：

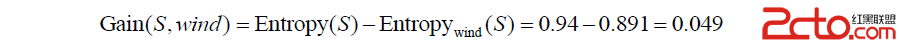
以上是求信息增益的步驟。其實 ID3 主要的難點就是求信息增益了。

 

 

樹的構建：

對於決策樹的構建，就如普通樹的構建一樣，利用遞歸建立節點就行。而 ID3 的特別之處就在於：在節點選擇屬性的時候，它總是選擇信息增益最大的那個屬性作為決策節點。

例如對於上文中的例子，基於 ID3 算法應該選用哪個屬性作為第一個決策節點？
解：求各個屬性對於目標屬性的信息增益：
Gain(S,outlook)=0.246，Gain(S, temperature)=0.029，Gain(S,humidity) =0.152，Gain(S,wind)=0.049
其中Gain(S,outlook)最大，所以選擇 outlook 屬性作為根節點。

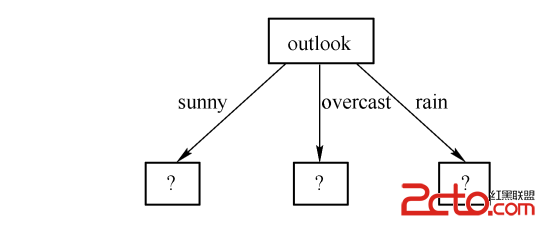
接下來對sunny分枝求哪個屬性作為子節點？
需要注意的是：此時用的數據集是子集Ssunny，而不是最初的那個weather數據集。

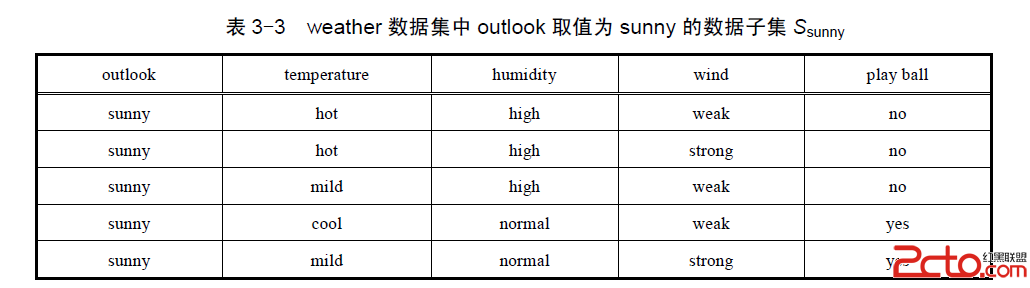
分別求temperature、humidity、wind對於目標屬性 play ball 的信息增益，然後取最大值作為子節點。
……
……
最終構建成的決策樹如下：

 

 

ID3的優缺點：

優點：

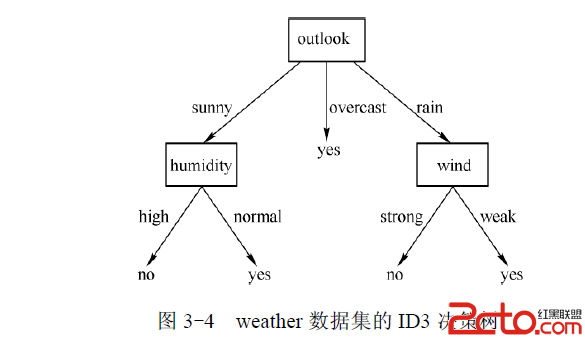
ID3的主要思想是：在決策樹的非葉子結點進行屬性選擇的時候，用信息增益作為選擇的標准，每一個非葉子結點都選擇當前的候選屬性中信息增益最大的那個屬性。這是貪心算法的思想，使得每一個非葉子結點在進行測試時都能獲得關於被測數據的最大類別信息，從而把整個決策樹的熵值降到最小。

缺點：

ID3只能處理離散型數據，無法處理連續性數據。例如上文中的wind屬性只有“strong”和“weak”兩個取值，是離散型的。如果換成用0~100的實數代表wind的強度，ID3 將無法處理。 如果某個屬性的數據含有缺失值，ID3 將無法處理。 信息增益的缺陷：信息增益在類別多的屬性上計算結果會大於類別少的屬性上的計算結果，這會導致 ID3 算法偏向選擇具有較多分枝的屬性，而分枝多的屬性不一定是最優的選擇。