樹型結構是一類非常重要的非線性數據結構,其中以樹和二叉樹最為常用,直觀看來,樹是以分支關系定義的層次結構。
樹的定義
樹(Tre)e是n(n>=0)個結點的有限集。在任意一棵非空樹中:
(1)有且僅有一個特定的稱為根(Root)的結點。
(2)當n>1時,其余結點可分為m(m>0)個互不相交的有限集T1,T2,...,Tm,其中每一個集合本身又是一棵樹,並且稱為根的子樹。
(3)樹的結點包含一個數據元素及若干指向其子樹的分支。
(4)結點擁有的子樹數稱為結點的度。
(5)度為0的結點稱為葉子或終端結點。
(6)度不為0的結點稱為非終端結點或分支結點。
(7)除根結點之外,分支結點也稱為內部結點。
(8)樹的度是樹內各結點的度的最大值。
(9)結點的子樹的根稱為該結點的孩子,相應地,該結點稱為孩子的雙親。同一個雙親的孩子之間互稱兄弟。
(10)結點的層次從根開始定義起,根為第一層,根的孩子為第二層。
(11)樹中各結點的最大層次稱為樹的深度或高度。
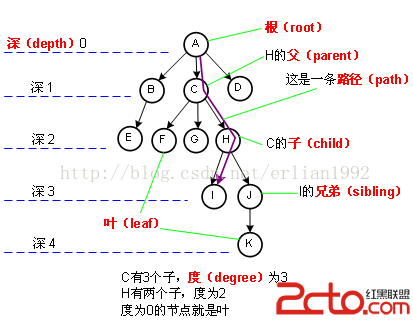
從上面的示例可以看出:
(1)這棵樹的根為A。
(2)這棵樹的深度或高度為5。
(3)這棵樹的層次為五層。
(4)這棵樹的葉子為:D,E,F,G,I,K。
(5)這棵樹的度為3,因為這棵樹中結點C有三個孩子並且為孩子最多的結點。
(6)這棵樹的內部結點為:B,C,D,E,F,G,H,I,J,K。
如果將樹結點的各子樹看成從左至右是有次序的(即不能替換),則稱該樹為有序樹,否則為無序樹。
森林是m(m>=0)棵互不相交的樹的集合。對樹中每個結點而言,其子樹的集合即為森林。
樹的基本操作:
InintTree(&T) 操作結果:構造空樹T DestroyTree(&T) 初始條件:樹T存在 操作結果:銷毀樹T CreateTree(&T,definition) 初始條件;definition給出樹的定義 操作結果:按definition構造樹 ClearTree(&T) 初始條件;樹T存在 操作結果:將樹T清空為樹 TreeEmpty(T) 初始條件:樹T存在 操作結果:若T為空樹,則返回TRUR,否則返回FALSE TreeDepth(T) 初始條件:樹T存在 操作結果:返回T的深度 Root(T) 初始條件:樹T存在 操作結果:返回T的根 Value(T,e) 初始條件:樹T存在,e是T中的某個結點 操作結果:返回e的值 Assign(T,e,value) 初始條件:樹T存在,e是T中的某個結點 操作結果:結點e賦值為value Parent(T,e) 初始條件:樹T存在,e是T中的某個結點 操作結果:若e是T的非根結點,則返回它的雙親,否則函數值為“空” LeftChild(T,e) 初始條件:樹T存在,e是T中的某個結點 操作結果:若e是T的非葉子結點,則返回它的最左孩子,否則函數值為“空” RightChild(T,e) 初始條件:樹T存在,e是T中的某個結點 操作結果:若e是T的非葉子結點,則返回它的最右孩子,否則函數值為“空” InsertChild(&T,&p,i,e) 初始條件:樹T存在,p指向T中的某個結點,1<=i<=p所指結點的度+1,非空樹c與T不相交 操作結果:插入c為T中p指結點的第i棵子樹 DeleteChild(&T,&p,i 初始條件:樹T存在,p指向T中某個結點,1<=i<=p指結點的度 操作結果:刪除T中p所指結點的第i棵子樹 TraverseTree(T,Visit()) 初始條件:樹T存在,Visit是對結點操作的應用函數 操作結果:按某種次序對T的每個結點調用函數Visit()一次且至多一次。一旦Visit()失敗,則操作失敗